本题链接:登录—专业IT笔试面试备考平台_牛客网
题目: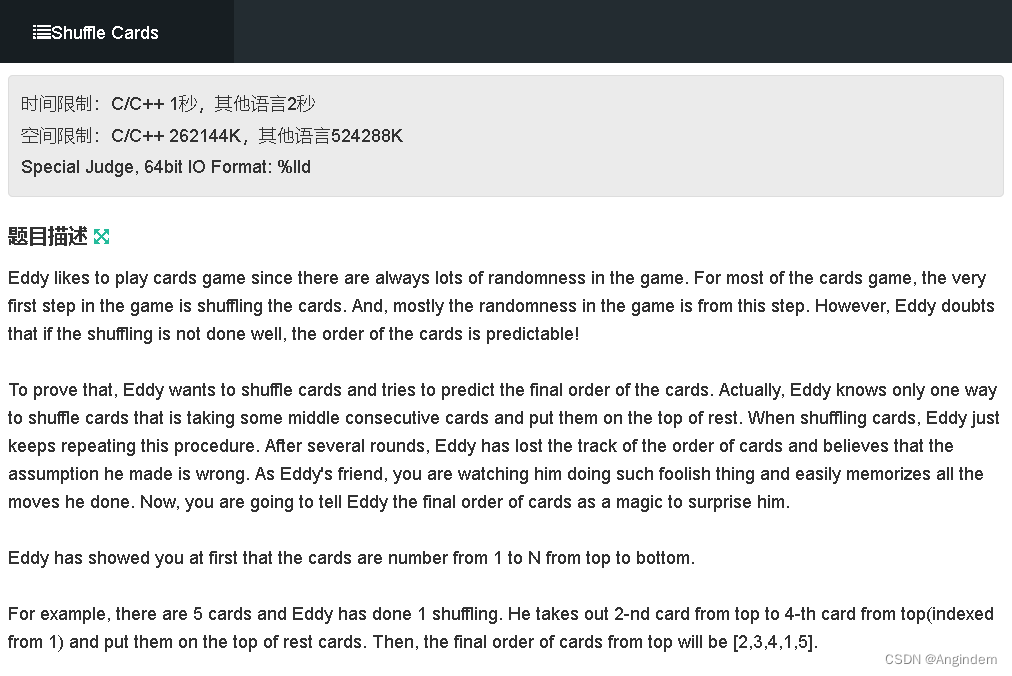

样例1:
|
| 2 3 4 1 5 |
样例2:
|
| 3 4 1 2 5 |
样例3:
|
| 3 4 1 5 2 |
思路:
这道题,其实就是个模拟题,根据题意。
第一行输入,n 为排列数 1~n,初始为递增序列,m 为操作次数。
随后 m 行,第一个数是 下标pos,第二个数是 长度 len。
每次切割以下标 pos 做起点到长度len 的数组拿取出来,放到前面,,问操作后的最终序列。
根据这题意,尝试模拟一遍,截取长度数组方面,有一个办法是将它们当作string进行截取删除放置操作。
模拟代码如下:
#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
#include <algorithm>
#include <unordered_map>
#define endl '\n'
#define int long long
#define YES puts("YES")
#define NO puts("NO")
#define umap unordered_map
#define All(x) x.begin(),x.end()
#pragma GCC optimize(3,"Ofast","inline")
#define IOS std::ios::sync_with_stdio(false),cin.tie(0), cout.tie(0)
using namespace std;
const int N = 2e6 + 10;
inline void solve();
signed main()
{
// freopen("a.txt", "r", stdin);
IOS;
int _t = 1;
// cin >> _t;
while (_t--)
{
solve();
}
return 0;
}
string s;
int n,m;
// 初始化序列
inline void Init()
{
for(int i = 1;i <= n;++i)
{
s += char(i + '0');
}
}
inline void Print_ans()
{
for(int i = 0;i < s.size();++i)
{
if(i) cout << ' ';
cout << s[i];
}
}
inline void solve()
{
cin >> n >> m;
Init();
while(m--)
{
int pos,len;
cin >> pos >> len;
pos -= 1; // 我们的 s 下标是以 0 开始,所以这里 -1
string tem = s.substr(pos,len); // 拿取这个区间的序列
s.erase(pos,len); // 删除以 pos作为起点,长度为len的序列
s = tem + s;
}
// 输出答案
Print_ans();
}提交后: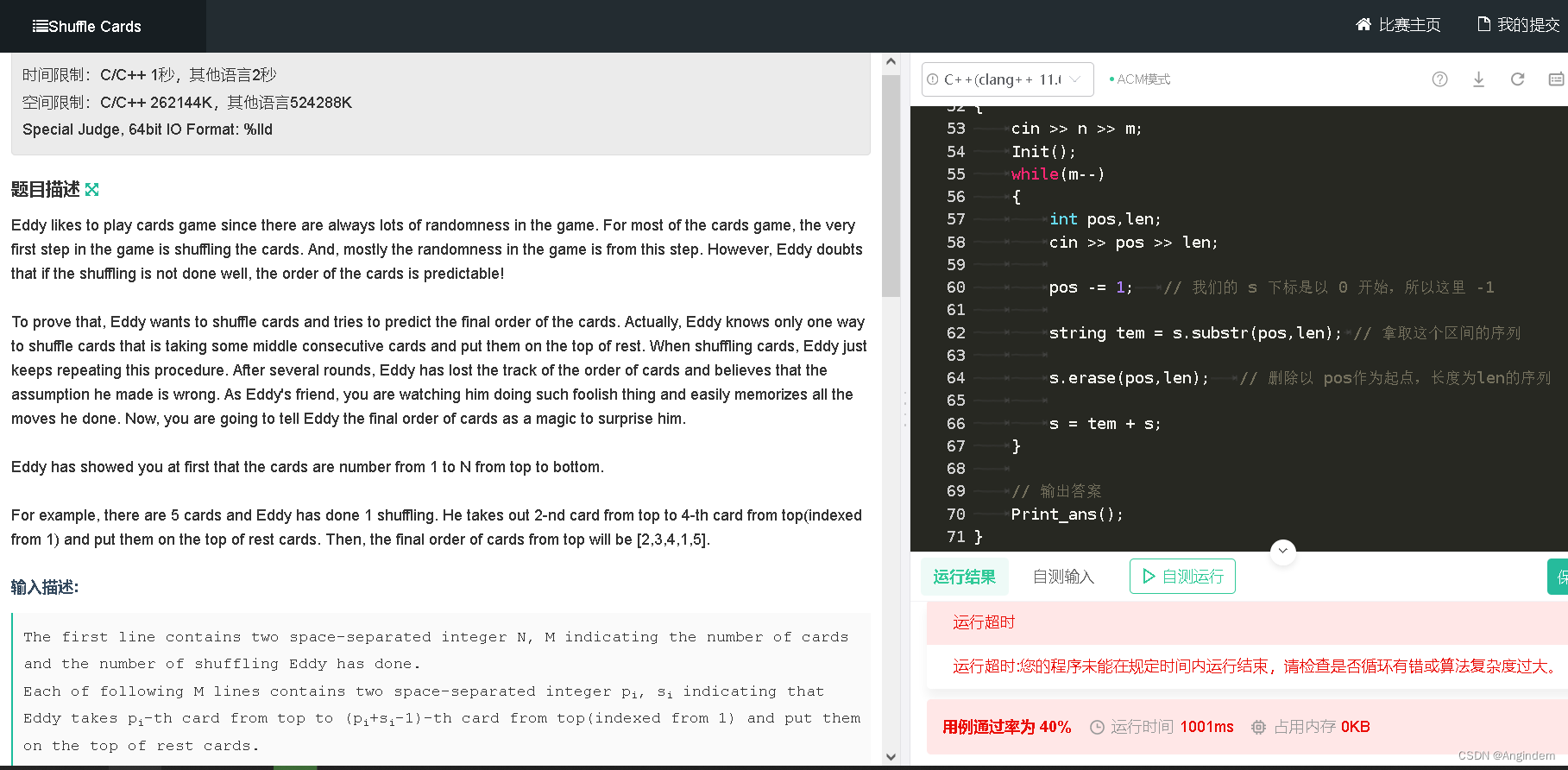
不出意料,超时了,这种明明是模拟题却出现超时的结果,这种情况就是需要一些特殊的数据结构了。
而这种结构之一,我们可以使用平衡树写法,平衡树的操作大部分都是 O(log n) 时间复杂度,而我们上面的代码string的操作时间复杂度是 O(n),所以很容易出现超时的现象。
那么根据平衡树,手写的话会很麻烦,其实,C++STL库中也内置了平衡树的操作,我们可以调用。具体操作如下:
rope平衡树具体操作:
#include<ext/rope>///头文件
using namespace __gnu_cxx;
rope <int> tree;
int main(){
int x = 2;
tree.push_back(x); //在末尾加x
tree.insert(pos, x); //在pos位置加入x
tree.erase(pos, len); //从pos位置删除len个元素
tree.copy(pos, len, x); //从pos开始len个元素用x代替
tree.replace(pos, x); //从pos开始全部换为x
tree.substr(pos, len); //提取pos开始len个元素
tree.at(i);tree[i]; //访问第x个元素
return 0;
}
并且rope< int>相当于一个块状链表。可以用substr等函数实现区间处理。
如果是rope< char>,相当于一个重型string。可以cout;可以+=。
rope最大的特点是支持可持久化。rope可以o(1)继承上一个版本。(内部维护了平衡树的指针)
最后要注意引用rope的细节:
#include <ext/rope>
using namespace __gnu_cxx;代码详解如下:
#include <iostream>
#include <ext/rope>
#define endl '\n'
#define int long long
#define All(x) x.begin(),x.end()
#pragma GCC optimize(3,"Ofast","inline")
#define IOS std::ios::sync_with_stdio(false),cin.tie(0), cout.tie(0)
using namespace std;
using namespace __gnu_cxx;
const int N = 2e6 + 10;
inline void solve();
signed main()
{
// freopen("a.txt", "r", stdin);
IOS;
int _t = 1;
// cin >> _t;
while (_t--)
{
solve();
}
return 0;
}
int n,m;
rope<int>tree; // 平衡树存值
// 初始化序列
inline void Init()
{
for(int i = 1;i <= n;++i) tree.push_back(i);
}
// 输出答案
inline void Print_ans()
{
for(int i = 0;i < (int)tree.size();++i)
{
if(i) cout << ' ';
cout << tree[i];
}
}
inline void solve()
{
cin >> n >> m;
Init();
while(m--)
{
int pos,len;
cin >> pos >> len;
pos -= 1; // 下标是以 0 开始,所以这里需要 -1
rope<int> tem = tree.substr(pos,len); // 截取区间序列
tree.erase(pos,len); // 删除区间序列,缩进序列
tree = tem + tree; // 放置前面
}
// 输出答案
Print_ans();
}