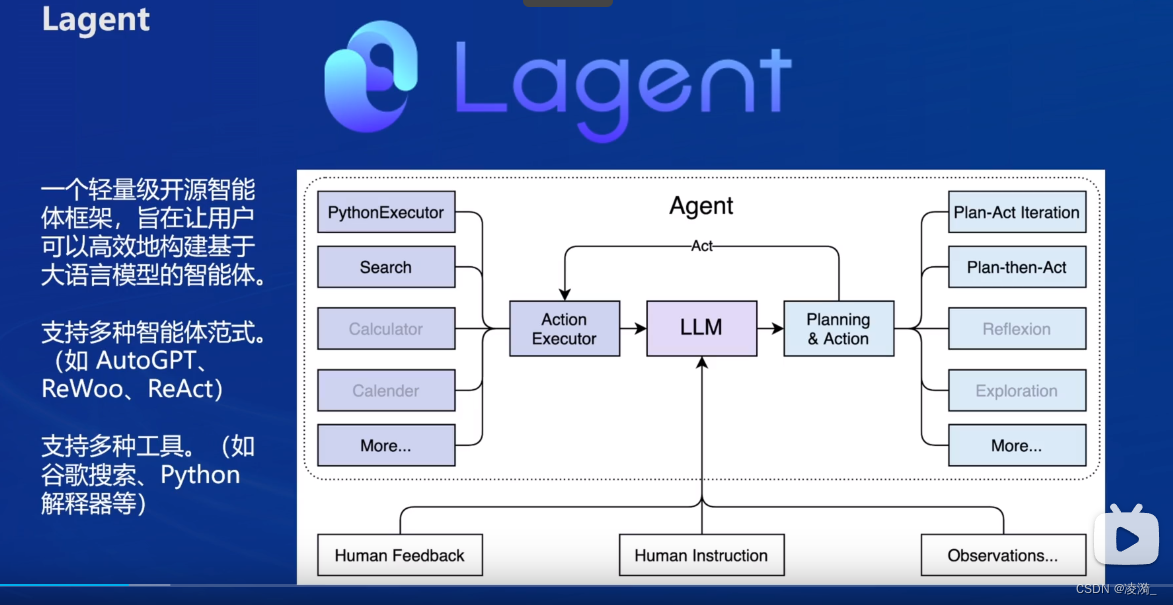
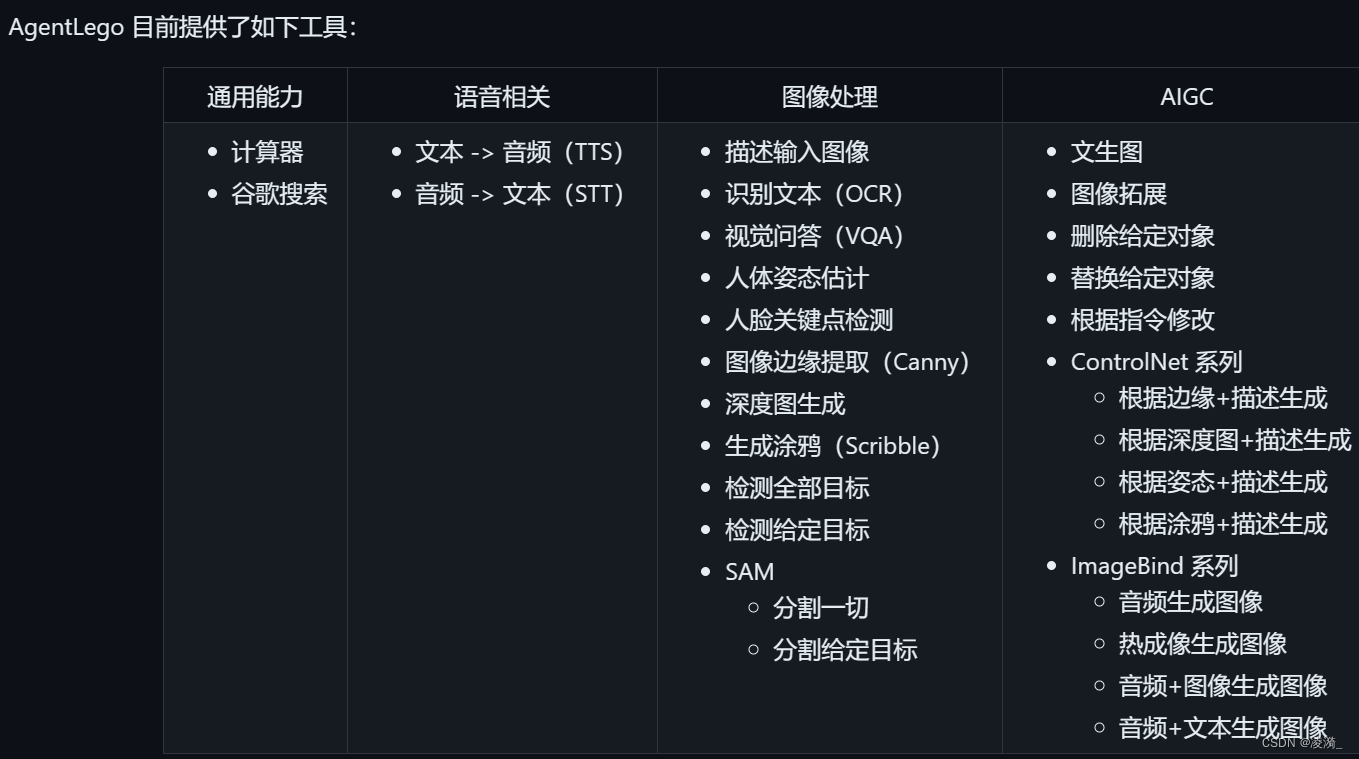
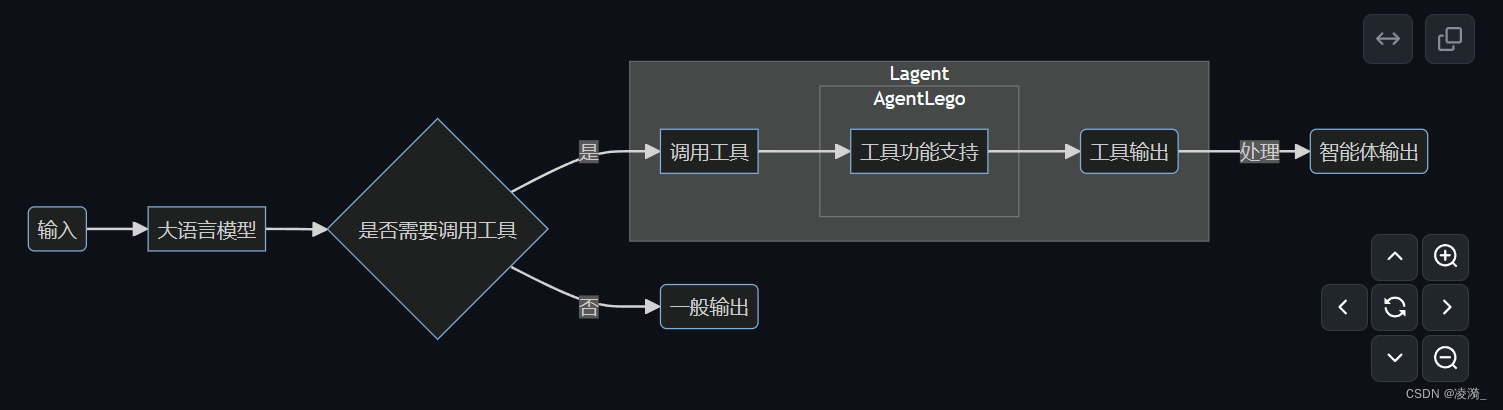
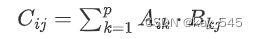【第6节课笔记】LagentAgentLego
news2026/2/17 12:10:59
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1652144.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
C++ | Leetcode C++题解之第74题搜索二维矩阵
题目: 题解:
class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int m matrix.size(), n matrix[0].size();int low 0, high m * n - 1;while (low < high) {int mid (high - low) / 2 l…
安卓玩机工具----一键备份手机分区 防止全檫除或者格机导致安全数据分区丢失
工具说明; 目前玩机root后有很多格机脚本。模块等等误刷会导致基带信号等等问题,在前面的博文中我有介绍过备份主要数据分区的重要性 。其实对于不了解root和不安装有些模块 外挂等等需要的友友不建议对手机进行root。root后对于手机安全性会有所降低。对于玩家来说…
信创 | 中国信创建设的历程与未来展望!
中国信创建设的历程与未来展望可以从多个维度进行分析。首先,从发展历程来看,中国信创产业的发展可以分为几个阶段。根据不同的资料来源,这些阶段的划分有所不同,但大体上可以概括为起步、试点、快速发展等关键时期。 起步阶段&am…
医疗器械软件如何生成符合FDA要求的SBOM文件?
在当今这个高度互联的世界,医疗器械的安全性和可靠性对于保障公众健康至关重要。FDA作为美国食品和药物的主要监管机构,长期以来一直致力于确保医疗器械的安全性和有效性。
2023年9月27日,美国食品和药品监督管理局(后续简称FDA&…
文本批量操作实例:如何实现文本批量拆分?实用方法与技巧分享
在文本处理和数据分析的过程中,我们经常会遇到需要批量拆分大量文本数据的情况。文本批量拆分能够大大提高工作效率,减少重复劳动。下面,我们将通过一个实例来介绍如何实现文本批量拆分,并分享一些实用方法与技巧。 一、实例背景 …
ESP32S3各个管脚使用需要注意的情况说明:
想使用ESP32S3做个控制电路,管脚使用情况自己整理了一下,记录一下,免得后面又忘记了,有不对之处望帮助更正: IO0和IO46先要说明一下:以前只注意IO0是启动刷机的时候用的,低电平时启动是串口刷机…
MT2050 矩阵01变
注意:
输入是直接输入了一行,所以不能使用for i{ for j {} },可以使用string 读一行然后挨个分析。
使用前缀和。
代码:
#include <bits/stdc.h>
using namespace std;
const int N 105;
int n, m;
int b[N][N];
strin…
如何在Hostease的Linux虚拟主机上永久移除WordPress网站
最近有遇到客户咨询如何移除Linux虚拟主机上的WordPress网站的, 因为原先的站点长时间不更新,被恶意篡改,跳转到了一个博彩网站上,本身网站也比较旧了,客户也不准备修复,准备重新建站。但是又怕移除不干净&…
【Django学习笔记(十)】Django的创建与运行
Django的创建与运行 前言正文1、安装Django2、创建项目2.1 基于终端创建项目2.2 基于Pycharm创建项目2.3 两种方式对比 3、默认项目文件介绍4、APP5、启动运行Django5.1 激活App5.2 编写URL和视图函数对应关系5.3 启动Django项目5.3.1 命令行启动5.3.2 Pycharm启动5.3.3 views.…
Re71:读论文 Sequence to Sequence Learning with Neural Networks
诸神缄默不语-个人CSDN博文目录 诸神缄默不语的论文阅读笔记和分类
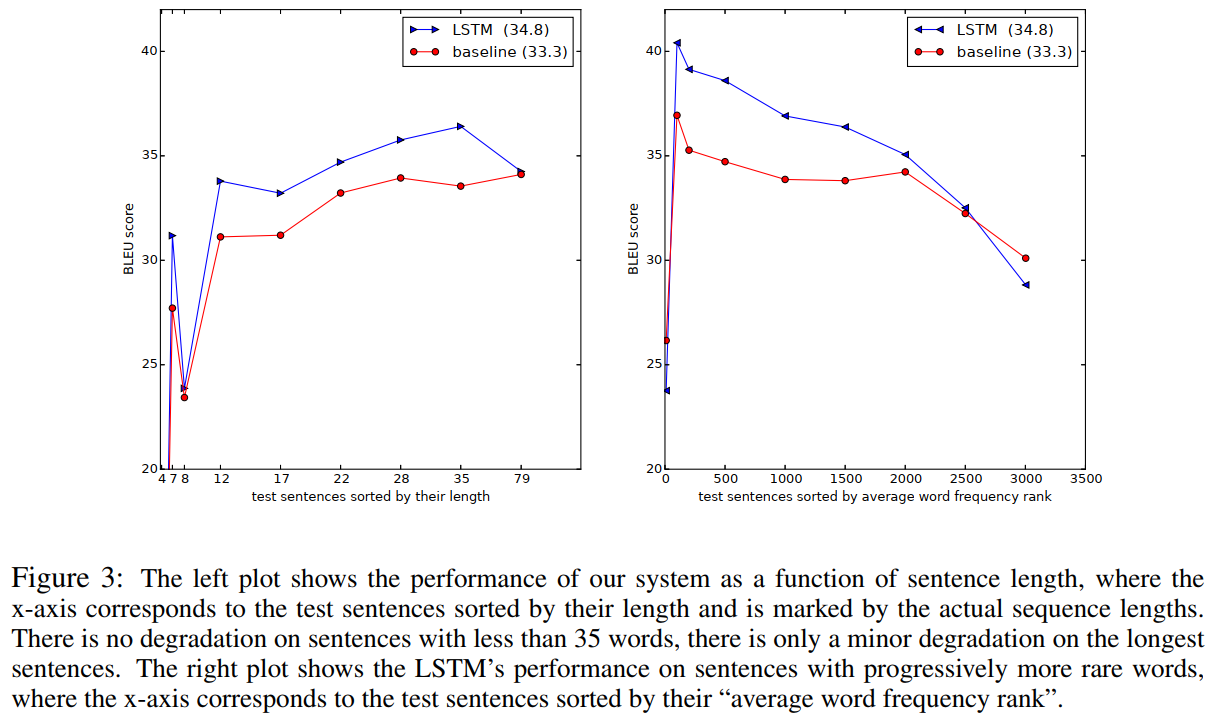
论文名称:Sequence to Sequence Learning with Neural Networks ArXiv下载地址:https://arxiv.org/abs/1409.3215
本文是2014年NeurIPS论文(那时候这个会还叫NIPS…
共享WiFi项目加盟骗局:共享WiFi贴码收益真的月入过万?
如今每个人的手机都是智能手机,我们几乎随时随地都需要网络的陪伴。而随着共享经济的概念深入人心,一种名为“共享WiFi贴码”的新兴事物逐渐走入了我们的视线。据说通过这种方式,人们可以实现轻资产创业,甚至有人声称能借此达到月…
ubuntu_Docker安装配置
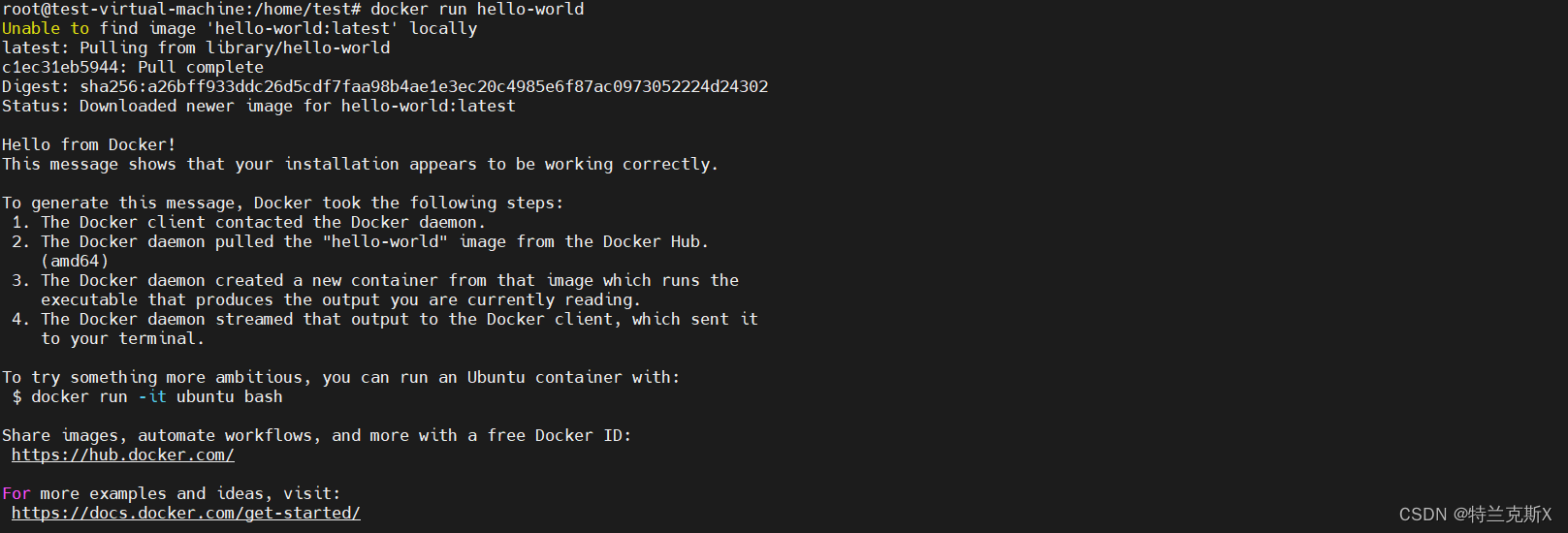
什么是docker?
Docker 是一个开源的应用容器引擎,让开发者可以打包他们的应用以及依赖包到一个可移植的镜像中,然后发布到任何流行的 Linux或Windows操作系统的机器上,也可以实现虚拟化。容器是完全使用沙箱机制,相互之间不会有…
百面算法工程师 | python解释器基础问答
本文给大家带来的百面算法工程师是深度学习python解释器面试总结,文章内总结了常见的提问问题,旨在为广大学子模拟出更贴合实际的面试问答场景。在这篇文章中,我们还将介绍一些常见的python用法,并提供参考的回答及其理论基础&…
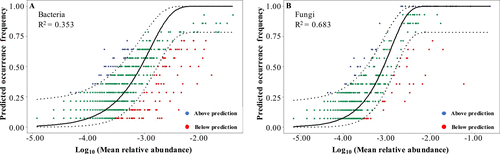
微生物群落构建(community assembly)
Introduction
Zhou, J. & Ning, D. Stochastic Community Assembly: Does It Matter in Microbial Ecology? Microbiol Mol Biol Rev 81, e00002-17 (2017). This review is very comprehensive (1)!
周集中老师实验室的长期研究兴趣集中在从基因组到生态系统…
史上最简单给大模型注入新知识的方法
《史上最简单给大模型注入新知识的方法》 image-20240508093410856 先执行 pip install --upgrade openai 。 from openai import OpenAI# 加载.env 文件到环境变量from dotenv import load_dotenv, find_dotenv_ load_dotenv(find_dotenv())# 初始化 OpenAI 服务。会自动从环…
MySQL增删查改(进阶)
目录
数据库约束
表的设计
查询操作的进阶
查询搭配插入使用
聚合查询
1>count(*)
2>sum(*)
3>avg(*)
4>max(*)
5>min(*)
group by分组分别进行聚合查询
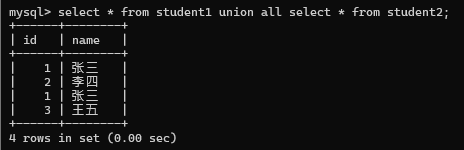
联合查询 / 多表查询[重点]
外连接
自连接
子查询
合并查询
小结: 数据库约束
有时候…
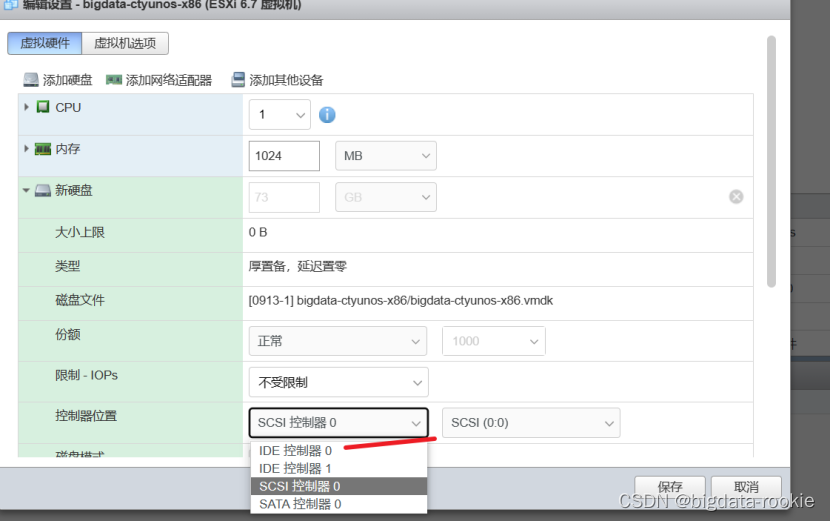
虚拟机镜像文件qcow2格式转vmdk
一、在esxi上虚拟机导出qcow2镜像文件
1、卸载数据盘、网卡
2、登录虚拟机所在物理服务器,查找系统盘名为vm-101-disk-0的文件位置
find / -name "vm-101-disk-0"使用命令导出qcow2镜像(进度条走完就完成了):
qemu…
基于FPGA的数字信号处理(10)--定点数的舍入模式(1)四舍五入round
1、前言
将浮点数定量化为定点数时,有一个避不开的问题:某些小数是无法用有限个数的2进制数来表示的。比如: 0.5(D) 0.1(B) 0.1(D) 0.0001100110011001~~~~(B) 可以看到0.5是可以精准表示的,但是0.1却不行。原因是整数是离散的…
蓝桥杯【第15届省赛】Python B组 32.60 分
F 题列表越界访问了……省一但没什么好名次 测评链接:https://www.dotcpp.com/oj/train/1120/
C 语言网真是 ** 测评,时间限制和考试的不一样,E 题给我整时间超限? A:穿越时空之门 100🏆
【问题描述】 随…