自动化机器学习——贝叶斯优化
贝叶斯优化是一种通过贝叶斯公式推断出目标函数的后验概率分布,从而在优化过程中不断地利用已有信息来寻找最优解的方法。在贝叶斯优化中,有两个关键步骤:统一建模和获得函数的优化。
1. 统一建模
在贝叶斯优化中,首先需要对目标函数进行建模,常用的建模方法包括:
-
高斯过程回归(Gaussian Process Regression): 将目标函数视为一个高斯过程,通过已有数据点来估计目标函数的均值和方差,从而构建一个高斯过程模型。
-
随机森林(Random Forest): 使用随机森林来拟合目标函数,通过集成多个决策树的预测结果来提高预测的准确性。
-
树形Parzen估计(Tree-structured Parzen Estimator,TPE): 使用树形结构来建模目标函数的条件分布,通过分层的贝叶斯方法来进行优化。
2. 获得函数的优化
获得函数是贝叶斯优化中的另一个关键步骤,它将后验分布转换成一个可优化的目标函数,用于选择下一个采样点。常用的获得函数包括:
-
期望改善(Expected Improvement,EI): 衡量当前最优解的期望改善程度,选择使期望改善最大的采样点作为下一个候选点。
-
置信区间优化(Confidence Bound,CB): 基于后验分布的置信区间来选择采样点,通常选择置信区间上界最大的点作为下一个候选点。
-
概率改善(Probability of Improvement,PI): 衡量当前最优解的概率改善程度,选择使概率改善最大的采样点作为下一个候选点。
示例代码
下面是一个简单的贝叶斯优化示例代码,使用高斯过程回归建模目标函数,并使用期望改善作为获得函数来选择下一个采样点。
import numpy as np
import matplotlib.pyplot as plt
# 目标函数
def target_function(x):
return np.sin(5 * x) / (1 + x**2)
# 高斯过程回归计算目标函数后验分布的方法
def calculate_posterior_distribution(X_train, y_train, X_test):
# 实现计算后验分布的方法
pass
# 贝叶斯优化的核心函数
def bayesian_optimization(objective_function, bounds, num_iterations=10):
# 实现贝叶斯优化的核心算法
pass
# 运行贝叶斯优化算法
bounds = (-2, 2)
X_train, y_train = bayesian_optimization(target_function, bounds)
# 可视化优化结果
x = np.linspace(-2, 2, 100)
y = target_function(x)
plt.plot(x, y, label='Target Function')
plt.scatter(X_train, y_train, color='red', label='Optimization Points')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Bayesian Optimization Result')
plt.legend()
plt.show()
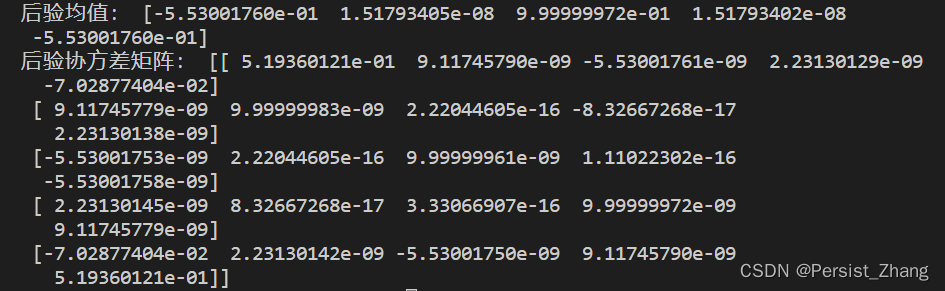
总结
贝叶斯优化是一种强大的优化方法,它通过建模目标函数的后验分布来不断地寻找最优解。本文介绍了贝叶斯优化的两个关键步骤:统一建模和获得函数的优化,并提供了一个简单的示例代码来演示其实现过程。贝叶斯优化在实际应用中具有广泛的应用价值,特别是在黑盒函数优化和高维空间搜索等问题中表现突出。