简介
拉依达检验法(3σ准则)是一种统计学方法,用于检测数据中的异常值。这种方法基于正态分布的特性来确定数据点是否可能是异常值。以下是关于拉依达检验法(3σ准则)的详细介绍:
-
基本原理:
- 拉依达检验法(3σ准则)假设一组检测数据只含有随机误差,通过对数据进行计算处理得到标准偏差σ(sigma)。
- 在正态分布中,数据点通常集中在均值μ(mu)附近,而标准偏差σ表示数据的离散程度。
- 根据正态分布的性质,大部分数据点(约68.26%)会分布在μ±σ之间,约有95.44%的数据点分布在μ±2σ之间,而几乎所有的数据点(约99.7%)都会分布在μ±3σ之间。
-
应用方法:
- 首先,计算数据的均值μ和标准偏差σ。
- 然后,确定一个区间,即μ±3σ。
- 任何超出这个区间的数据点被认为是异常值,可能由于粗大误差或过失误差引起,这些异常值应予以剔除或进行进一步检查。
-
适用范围与局限性:
- 拉依达检验法(3σ准则)主要适用于正态或近似正态分布的数据集。
- 该方法以测量次数充分大为前提,当测量次数较少时,使用此方法剔除粗大误差可能不够可靠。
- 因此,在数据量较小的情况下,应谨慎使用此方法,并可能需要选择其他更适用的方法。
这一个版本的代码,针对之前代码[1]的不足和问题,对程序进行了进一步的优化。
[1]:matlab 基于拉依达检验法(3σ准则) 实现多类别多参数的批量检验异常值与异常样本_拉依达准则matlab-CSDN博客
代码简介和说明
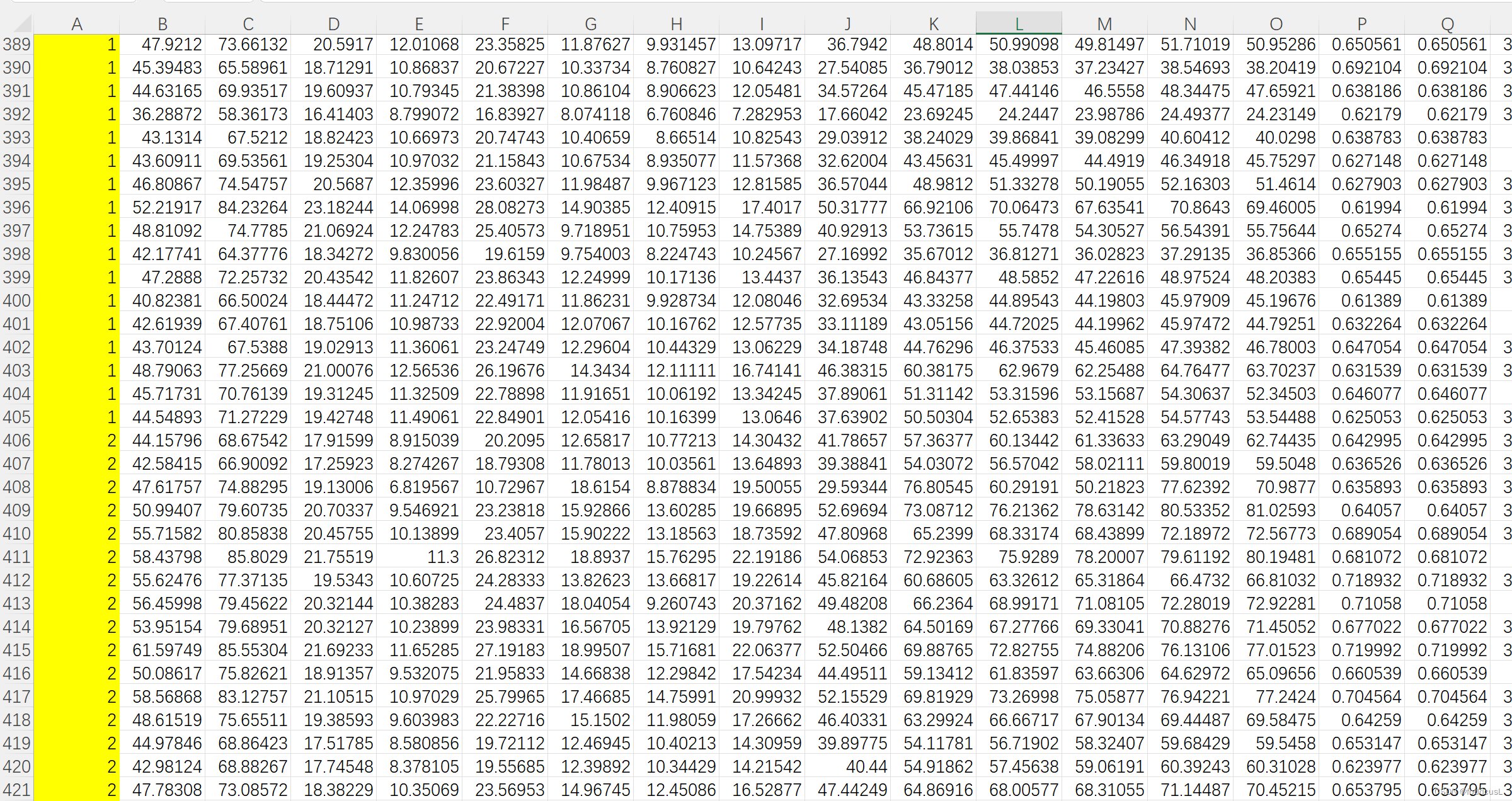
输入数据:
数据每行代表一个样本,每列代表一个参数
输入数据的第一列为类别表示,即同一类别用相同的数字标识:
主程序:
%拉伊达检验法;不同样本在不同行,不同参数不同列
%输入 data:数据表格,其中第1列为标识
%输出:Errorshow 异常样本所在的行数,以及异常的参数内容(列)
%输入:resData 剔出异常样本后的表格
clear all
%%参数设置区域
data=xlsread("test.xlsx");%输入表格
%按数字标识的方法
nameNum=[1,2,3,4,5,6];%输入每个处理数字标识,自己可以设定(","衔接)
[~,classNum]=size(nameNum);
maxCheck_num=100;%最大循环检验次数
%%
[maxrow,~]=size(data);
data=[(1:maxrow)',data];%增加序号标识
for i=1:classNum%遍历不同的处理
indexlist=find(data(:,2)==nameNum(1,i));
testdata=data(indexlist,:);
[IFPa,ErrorRowindex{i},res]=patuaC(testdata,maxCheck_num,nameNum(i));
if i==1
resdata=res;
else
resdata=[resdata;res];
end
end
%将异常样本整合在一个表中展示
Errorshow=zeros(1,length(data(1,:)));
for i=1:classNum%类别
for p=3:length(data(1,:))%参数
for j=1:length(ErrorRowindex{i}{p-2}())%行号
Errordet=zeros(1,length(data(1,:)));
if ErrorRowindex{i}{p-2}(j)~=0
if ismember(ErrorRowindex{i}{p-2}(j),Errorshow(:,1))
Errorshow( find(Errorshow(:,1)==ErrorRowindex{i}{p-2}(j)) ,p-1)=1;
else
Errordet(1,1)=[ErrorRowindex{i}{p-2}(j)];
Errordet(1,p-1)=1;
Errorshow=[Errorshow;Errordet];
end
end
end
end
end
Errorshow=sortrows(Errorshow,1);%排序
自定义函数patuaC
(将其放入和主程序同一文件夹内后运行主程序)
function [IFPa,ErrorRowindex,resdata]=patuaC(inputdata,maxCheck_num,classindex)
%输入:
% inputdata:检验的数据
%maxCheck_num:最大迭代次数
%classindex:样本代号
%输出:
%IFPa:逻辑值,是否有异常样本
%ErrorRowindex:异常样本的位置信息
%resdata:剔除异常值剩余的数据
% 此处显示详细说明
resdata=inputdata;
for i=1:maxCheck_num
[yn,xn]=size(resdata);
Slist=std(resdata);%计算方差和均值
Ave=mean(resdata);
IFPacir=false;
for coln=3:xn
ErrorRow{coln-2}=[0];
for rown=1:yn
if abs(resdata(rown,coln)-Ave(coln))>3*Slist(coln)
IFPacir=true;
ErrorRow{coln-2}=[ErrorRow{coln-2};resdata(rown,1)];
end
end
end
if IFPacir%如果有问题数据
%删除有问题的行
for coln=1:xn-2
if i~=1
ErrorRowindex{coln}=[ErrorRowindex{coln};ErrorRow{coln}];
else
ErrorRowindex{coln}=ErrorRow{coln};
end
[cirN,~]=size(ErrorRow{coln});
for dn=1:cirN
if ismember(ErrorRow{coln}(cirN),resdata(:,1))
resdata(find(resdata(:,1)==ErrorRow{coln}(cirN)),:)=[];
end
end
end
else
break
end
end
abnormal_samples = length(inputdata(:,1)) - length(resdata(:,1));
if abnormal_samples~=0
IFPa=true;
end
percentN=(length(inputdata(:,1)) - length(resdata(:,1)))/length(inputdata)*100;
message = sprintf('在类别"[%d]"中找到 %d 个异常样本,占比%.2f%%', classindex,abnormal_samples,percentN);
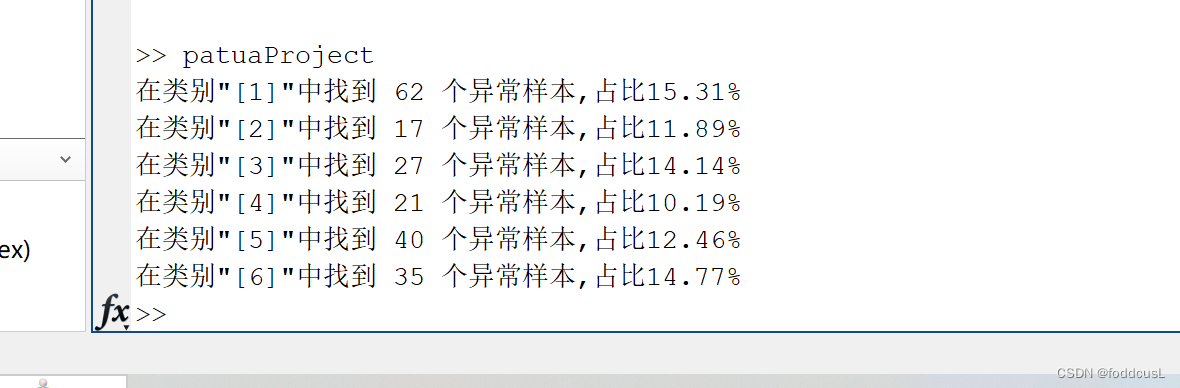
disp(message);执行效果:
控制窗输出异常样本信息:
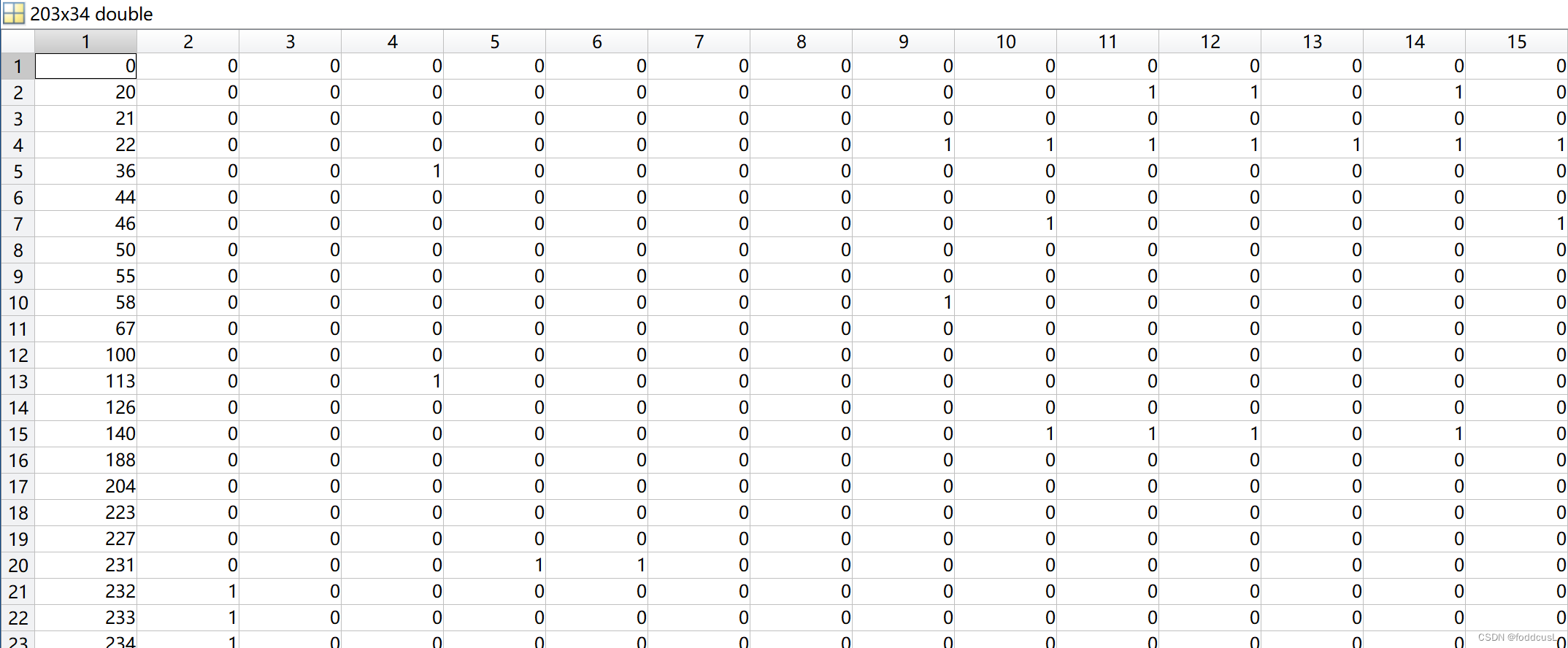
异常样本的整合信息Errorshow:
第一行是异常样本原来所在的行号,对应的列为1代表该列的参数不满足检验假设;
数据分享:
我将脚本使用的检验数据分享给各位,方便复现和了解:
链接:https://pan.baidu.com/s/1_OGMMluQgusFV66v-4xOQQ?pwd=cvws
提取码:cvws