代码随想录Day 40|Leetcode|Python|139.单词拆分 ● 关于多重背包，你该了解这些！ ● 背包问题总结篇！

news2024/11/27 4:36:42

139.单词拆分

给你一个字符串 s 和一个字符串列表 wordDict 作为字典。如果可以利用字典中出现的一个或多个单词拼接出 s 则返回 true。

注意：不要求字典中出现的单词全部都使用，并且字典中的单词可以重复使用。

解题思路：

确定dp数组含义：dp[i]当字符串长度为i时，是否可以利用字典拼出当前子串s[:i]，1的话可以

确定递推公式：如果要判断当前长度i时dp是否为1，可以通过判断 j 时dp的状态和s[j:i]是否在字典里，在的话dp[i] = true（查看最近的dp值为1和该值与当前遍历长度之间的子串是否在字典里

初始化：dp[0] = True, dp[i] = 0

遍历顺序：从前到后，本题是排列问题，相同字符只用出现一次，先遍历背包再遍历物品。

打印dp数组：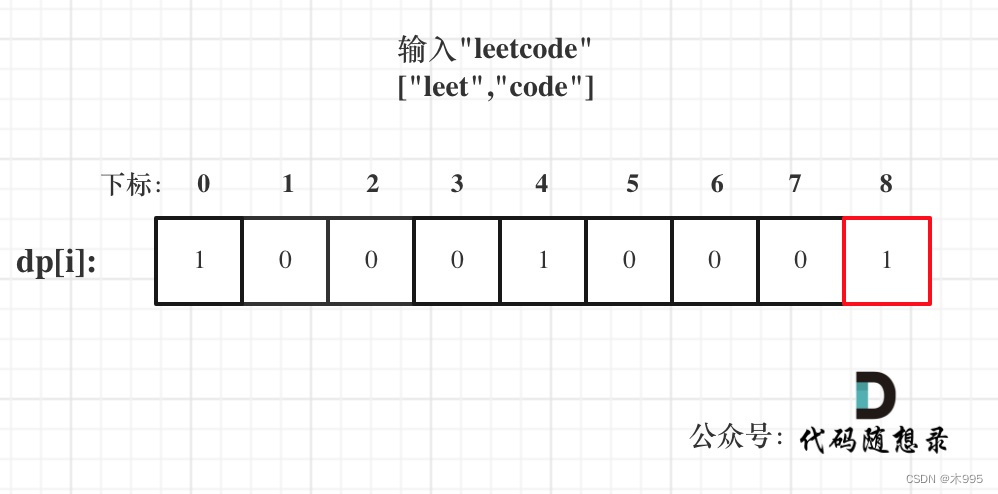

class Solution:
    def wordBreak(self, s: str, wordDict: List[str]) -> bool:
        dp = [0]*(len(s)+1)
        dp[0] = 1
        #先遍历背包
        for j in range(1,len(s)+1):
            #遍历物品
            for i in range(j+1):
                if dp[i]==1 and (s[i:j] in wordDict):
                    dp[j] = 1
        return dp[len(s)] == 1

关于多重背包，你该了解这些！

来源：代码随想录 (programmercarl.com)

有N种物品和一个容量为V 的背包。第i种物品最多有Mi件可用，每件耗费的空间是Ci ，价值是Wi 。求解将哪些物品装入背包可使这些物品的耗费的空间总和不超过背包容量，且价值总和最大。

多重背包和01背包是非常像的，为什么和01背包像呢？

每件物品最多有Mi件可用，把Mi件摊开，其实就是一个01背包问题了。

例如：

背包最大重量为10。

物品为：

	重量	价值	数量
物品0	1	15	2
物品1	3	20	3
物品2	4	30	2

问背包能背的物品最大价值是多少？

和如下情况有区别么？

	重量	价值	数量
物品0	1	15	1
物品0	1	15	1
物品1	3	20	1
物品1	3	20	1
物品1	3	20	1
物品2	4	30	1
物品2	4	30	1

题目描述56. 携带矿石资源（第八期模拟笔试） (kamacoder.com)

你是一名宇航员，即将前往一个遥远的行星。在这个行星上，有许多不同类型的矿石资源，每种矿石都有不同的重要性和价值。你需要选择哪些矿石带回地球，但你的宇航舱有一定的容量限制。

给定一个宇航舱，最大容量为 C。现在有 N 种不同类型的矿石，每种矿石有一个重量 w[i]，一个价值 v[i]，以及最多 k[i] 个可用。不同类型的矿石在地球上的市场价值不同。你需要计算如何在不超过宇航舱容量的情况下，最大化你所能获取的总价值。

输入描述

输入共包括四行，第一行包含两个整数 C 和 N，分别表示宇航舱的容量和矿石的种类数量。

接下来的三行，每行包含 N 个正整数。具体如下：

第二行包含 N 个整数，表示 N 种矿石的重量。

第三行包含 N 个整数，表示 N 种矿石的价格。

第四行包含 N 个整数，表示 N 种矿石的可用数量上限。

输出描述

输出一个整数，代表获取的最大价值。

输入示例

输出示例

解题思路：

本题是一个多重背包问题，可以转化成零一背包问题。参考以上表格将这些物品数量全都变成1，使物品重复出现在list里，以下代码将数量大于一的物品展开运算，可能会超时：

c, n = map(int, input().split())
weights = [x for x in map(int,input().split())]
values = [x for x in map(int,input().split())]
quanties = [x for x in map(int,input().split())]
# print(values, quanties)
for i in range(len(quanties)):
    while quanties[i]>1:
        weights.append(weights[i])
        values.append(values[i])
        quanties[i] -= 1
# print(weights, values)#convert to 0-1 bag problems
dp = [0]*(c+1)
def bag():
    for i in range(len(weights)):
        for j in range(c, weights[i]-1, -1):
            dp[j] = max(dp[j], dp[j-weights[i]]+values[i])
    print(dp)
    print(dp[c])
bag()

因此需要遍历时将物品数量纳入考虑：

c, n = map(int, input().split())
weights = [x for x in map(int,input().split())]
values = [x for x in map(int,input().split())]
quanties = [x for x in map(int,input().split())]

dp = [0]*(c+1)
def bag():
    for i in range(len(weights)):
        for j in range(c, weights[i]-1, -1):
            k = 1
            while k<=quanties[i] and (j-k*weights[i]>= 0):
                dp[j] = max(dp[j], dp[j-k*weights[i]]+values[i]*k)
                # print(dp)
                k += 1
    # print(dp)
    print(dp[c])
bag()

时间复杂度：O(m × n × k)，m：物品种类个数，n背包容量，k单类物品数量