🔮题目一描述：扑克牌消消乐

塔子哥最新沉迷某三消游戏，现在的他已经是这方面的大神。你太想进步了，找到了塔子哥并求他传授秘籍。他决定用一个游戏测试一下你的功底。

塔子哥从一副扑克牌中随机抽取n张牌组成一个序列，规定：连续3张相同牌号的卡牌可以消除，剩余卡牌按照当前顺序重新合并成新的序列后继续消除，例如序列 01112 在消除 111 之后，余下 02，重复以上步骤直到无法消除，请你完成这个游戏，输出结束后剩余的卡牌序列。

注：存在连续4张相同牌号的情况，消除后剩余一张。

输入描述

第一行输入一个整数n，表示抽出扑克牌的数量。其中$1\le n\le 52$。

第二行一个字符串，以空格分隔代表卡牌号序列，卡牌号仅包含2-10，A，J，Q，K

输出描述

输出一个字符串，表示最终的卡牌序列，卡牌号以空格分隔。

当所有扑克牌都被消除，输出0

样例一

输入

10
6 2 3 3 3 2 2 2 7 7 7

输出

6 2

样例二

输入

6 
5 A A A 5 5

输出

0

Limitation

1s, 1024KiB for each test case.

OJ链接：
https://codefun2000.com/p/P1827

解题思路一：模拟，遇到连续3张相同牌号的卡牌，直接删除

n = int(input())
strs = list(map(str, input().split()))

i = 0
while i < len(strs):
    if i + 2 < len(strs):
        if strs[i] == strs[i + 1] and strs[i + 1] == strs[i + 2]:
            strs = strs[:i] + strs[i+3:]
            if i > 0:
            	i -= 1
            continue
        i += 1
    else:
        break
if len(strs) == 0:
    print(0)
else:
    for s in strs:
        print(s, end = ' ')

时间复杂度：O(n) 一次遍历
空间复杂度：O(1) 输出答案不算

解题思路二：栈

n = int(input())
stack = []
a = input().split()
for i in a:
    if len(stack) < 2:
        stack.append(i)
    else:
        if stack[-1] == i and stack[-2] == i:
            stack.pop(-1)
            stack.pop(-1)
        else:
            stack.append(i)

print(' '.join(stack))

时间复杂度：O(n)
空间复杂度：O(1)

解题思路三：c++， java

#include<bits/stdc++.h>
using namespace std;
int main(){
int n;
cin>>n;
vector<char>a;
for(int i=0;i<n;i++){
    char c;
    cin>>c;
    a.push_back(c);
}
while(a.size()>=3){
    int flag=-1;
    for(int i=0;i<a.size()-2;i++){
        if(a[i]==a[i+1]&&a[i]==a[i+2]){
            flag=i;
            break;
        }
    }
    if(flag==-1)break;
    a.erase(a.begin()+flag,a.begin()+flag+3);
}
for(int i=0;i<a.size();i++){
    cout<<a[i];
    if(i!=a.size()-1)cout<<" ";
}


    return 0;
}

# java
import java.util.Scanner;
import java.util.Stack;

public class Main {
    public static void main(String[] args) {
        Scanner s = new Scanner(System.in);
        String a = s.nextLine();
        int n = Integer.parseInt(a);
        String b = s.nextLine();
        String[] xulie = b.split(" ");
        Stack<String> stack = new Stack<>();
        Stack<Integer> count = new Stack<>();

        for (int i = 0; i < xulie.length; i++) {
            if (stack.isEmpty()) {
                stack.push(xulie[i]);
                count.push(1);
                continue;
            }
            if (stack.peek().equals(xulie[i])) {
                stack.push(xulie[i]);
                count.push(count.peek() + 1);
                if (count.peek() == 3){
                    stack.pop();
                    stack.pop();
                    stack.pop();
                    count.pop();
                    count.pop();
                    count.pop();
                }
                continue;
            }
            if (!stack.peek().equals(xulie[i])) {
                stack.push(xulie[i]);
                count.push(1);
            }
        }
        if (stack.isEmpty()) {
            System.out.print("0");
            return;
        }
        String[] result = new String[stack.size()];
        int i = 0;
        while (!stack.isEmpty()) {
            result[i] = stack.pop();
            i++;
        }
        for (int i1 = result.length - 1; i1 >= 0; i1--) {
            System.out.print(result[i1]);
            if (i1 != 0){
                System.out.print(" ");
            }
        }
    }
}

时间复杂度：O(n)
空间复杂度：O(1)

⚗️题目二描述：公司部门风险评估

LYA 是一家大型科技公司的风险评估师。公司的部门结构可以看作一棵树，每个部门在评估前都有一些尚未解决的问题。部门的风险值可以用来评估该部门是否存在风险，风险值的计算公式为：风险值 = 5 × 严重问题数 + 2 × 一般问题数。

其中，每个部门的不同级别问题数量需要将该部门及其下属部门的相应级别问题数量求和。当部门的风险值小于等于给定的阈值时，该部门被认为是安全的；否则，该部门被视为风险部门，需要进一步整改。

现在给出公司的部门结构以及各部门的问题数量，请你帮助 LYA 计算出风险部门的数量。

输入描述

第一行包含两个正整数 M 和 N（$1\le M\le 100000$，$1\le N\le 1000$），分别表示风险阈值和部门的数量。

接下来 N 行，每行包含四个字段，用空格分隔：

• 第一个字段为部门名称 $A_i$；
• 第二个字段为 $A_i$ 的上级部门名称$B_i$，如果 $A_i$为公司的最高层部门，则 $B_i$用 *表示；
• 第三个字段为问题级别 $C_i$（ C i ∈ { 0 , 1 } C_i \in \{0, 1\} Ci​∈{0,1}，其中 0表示严重问题，1表示一般问题）；
• 第四个字段为该部门该级别的问题数量 $D_i$（$1\le D_i\le 1000$）。

其中，$A_i$和 $B_i$为由小写英文字母组成的字符串，长度不超过 5。

输入保证部门结构为一棵树，不会出现环的情况。

输出描述

输出一个整数，表示风险部门的数量。

样例一

输入

40 12 
a * 0 2 
a * 1 2 
b a 0 3 
b a 1 5 
c a 1 3 
d a 0 1 
d a 1 3 
e b 0 2 
f * 0 8 
f * 1 10 
g f 1 2
h * 0 4

输出

2

解释

（a * 0 2）表示节点a有2个严重问题，*表示无父节点，即a为云服务。（b a 1 5）表示节点b有5个一般问题，b的父节点是a。可以看出，该样例有3个云服务a、f、h。云服务a的子节点有b、c、d、e，严重问题个数为2+3+0+1+2=82+3+0+1+2=8，一般问题个数为2+5+3+3+0=132+5+3+3+0=13，DI值=8∗5+13∗2=66>阈值40，故云服务a是风险云服务；云服务f严重问题个数为8+0=88+0=8，一般问题个数为10+2=1210+2=12，DI值=8∗5+12∗2=64>阈值40，故云服务f也是风险云服务；云服务h严重问题个数为44，一般问题个数为00，DI值=4∗5+0∗2=20<=阈值40，故云服务h不是风险云服务；因此该样例有2个风险云服务。

样例二

输入

50 10 
b a 1 5 
a * 0 2 
b a 0 3 
c a 1 3 
d a 0 1 
a * 1 2 
d a 1 3 
e b 0 2 
f b 1 1 
g c 1 2

输出

1

数据范围

• $1\le M\le 100000$
• $1\le N\le 1000$
• $1\le D_i\le 1000$
• $A_i$和 $B_i$为由小写英文字母组成的字符串，长度不超过 5。

Limitation

1s, 1024KiB for each test case.

OJ链接：
https://codefun2000.com/p/P1828

解题思路一：dfs

本题可以使用树形 DP 的思想来解决。可以从叶子节点开始，自底向上计算每个部门的严重问题数和一般问题数，然后根据风险值的计算公式判断该部门是否为风险部门。

具体步骤如下：

1. 建立部门之间的父子关系，使用邻接表或者邻接矩阵来存储。
2. 对于每个部门，初始化其严重问题数和一般问题数。
3. 从叶子节点开始，通过 DFS 或 BFS 遍历整棵树，对于每个部门：
   • 将其子部门的严重问题数和一般问题数累加到当前部门上。
   • 计算当前部门的风险值，并判断是否超过阈值，如果超过则将风险部门数量加 1。
4. 输出风险部门的数量。

from collections import defaultdict
M, N = map(int, input().split())
graph = defaultdict(list) # 邻接表，记录子节点
risks0 = defaultdict(int) # 严重问题
risks1 = defaultdict(int) # 一般问题

roots = set()
for _ in range(N):
    node, parent, level, num = input().split()
    num = int(num)
    if parent == '*':
        roots.add(node)
    else:
        graph[parent].append(node)
    if level == '0':
        risks0[node] = num
    else:
        risks1[node] = num

def dfs(node):
    risk0, risk1 = risks0[node], risks1[node]
    for ch in graph[node]:
        ch_risk0, ch_risk1 = dfs(ch)
        risk0 += ch_risk0
        risk1 += ch_risk1
    return risk0, risk1

cnt = 0
for root in roots:
    risk0, risk1 = dfs(root)
    if 5 * risk0 + 2 * risk1 > M:
        cnt += 1
print(cnt)

时间复杂度：O(n) 其中 n 为部门的数量。
空间复杂度：O(n)

解题思路二：bfs

from collections import defaultdict, deque
M, N = map(int, input().split())
graph = defaultdict(list) # 邻接表，记录子节点
risks0 = defaultdict(int) # 严重问题
risks1 = defaultdict(int) # 一般问题

roots = set()
for _ in range(N):
    node, parent, level, num = input().split()
    num = int(num)
    if parent == '*':
        roots.add(node)
    else:
        graph[parent].append(node)
    if level == '0':
        risks0[node] = num
    else:
        risks1[node] = num

def bfs(node):
    risk0, risk1 = risks0[node], risks1[node]
    queue = deque([node])
    while queue:
        node = queue.pop()
        for ch in graph[node]:
            queue.append(ch)
            ch_risk0, ch_risk1 = risks0[ch], risks1[ch]
            risk0 += ch_risk0
            risk1 += ch_risk1
    return risk0, risk1

cnt = 0
for root in roots:
    risk0, risk1 = bfs(root)
    if 5 * risk0 + 2 * risk1 > M:
        cnt += 1
print(cnt)

时间复杂度：O(n)
空间复杂度：O(n)

解题思路三：java, c++

import java.util.*;

public class Main {
    static Map<String, List<String>> graph = new HashMap<>();
    static Map<String, Integer> risks1 = new HashMap<>();
    static Map<String, Integer> risks2 = new HashMap<>();

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int m = sc.nextInt();
        int n = sc.nextInt();
        sc.nextLine();

        Set<String> roots = new HashSet<>();
        for (int i = 0; i < n; i++) {
            String[] input = sc.nextLine().split(" ");
            String dept = input[0];
            String parent = input[1];
            int level = Integer.parseInt(input[2]);
            int num = Integer.parseInt(input[3]);

            if (parent.equals("*")) {
                roots.add(dept);
            } else {
                graph.computeIfAbsent(parent, k -> new ArrayList<>()).add(dept);
            }

            if (level == 0) {
                risks1.put(dept, num);
            } else {
                risks2.put(dept, num);
            }
        }

        int cnt = 0;
        for (String root : roots) {
            int[] risks = dfs(root);
            if (5 * risks[0] + 2 * risks[1] > m) {
                cnt++;
            }
        }

        System.out.println(cnt);
    }

    private static int[] dfs(String dept) {
        int risk1 = risks1.getOrDefault(dept, 0);
        int risk2 = risks2.getOrDefault(dept, 0);

        for (String sub : graph.getOrDefault(dept, new ArrayList<>())) {
            int[] subRisks = dfs(sub);
            risk1 += subRisks[0];
            risk2 += subRisks[1];
        }

        return new int[]{risk1, risk2};
    }
}

#include <iostream>
#include <unordered_map>
#include <unordered_set>
#include <vector>
#include <string>

using namespace std;

unordered_map<string, vector<string>> graph;
unordered_map<string, int> risks1;
unordered_map<string, int> risks2;

pair<int, int> dfs(const string& dept) {
    int risk1 = risks1[dept];
    int risk2 = risks2[dept];

    for (const string& sub : graph[dept]) {
        auto subRisks = dfs(sub);
        risk1 += subRisks.first;
        risk2 += subRisks.second;
    }

    return {risk1, risk2};
}

int main() {
    int m, n;
    cin >> m >> n;

    unordered_set<string> roots;
    for (int i = 0; i < n; i++) {
        string dept, parent;
        int level, num;
        cin >> dept >> parent >> level >> num;

        if (parent == "*") {
            roots.insert(dept);
        } else {
            graph[parent].push_back(dept);
        }

        if (level == 0) {
            risks1[dept] = num;
        } else {
            risks2[dept] = num;
        }
    }

    int cnt = 0;
    for (const string& root : roots) {
        auto risks = dfs(root);
        if (5 * risks.first + 2 * risks.second > m) {
            cnt++;
        }
    }

    cout << cnt << endl;

    return 0;
}

时间复杂度：O(n)
空间复杂度：O(n)

🎀题目三描述：城市应急疏散

LYA 是一名城市应急管理专家，她负责制定城市在发生重大事故时的疏散计划。城市由 n 个区域组成，每个区域之间都有道路相连。当某个区域发生事故需要疏散时，LYA 需要选择一个或多个安全区域作为疏散目的地，并确保疏散路径的总长度最短。

给定一个$n\times n$ 的矩阵 dist，其中 $dist[i][j]$ 表示区域 i 到区域 j 的道路长度，如果 $dist[i][j]=-1$，则表示区域 i 和区域 j 之间没有直接相连的道路。另外，每个区域还有一个剩余容量 $cap[i]$，表示该区域最多可以容纳的人数。

当某个区域 x 发生事故需要疏散人数为 p 时，请你帮助 LYA 选择疏散区域，使得疏散路径的总长度最短，并且疏散区域的剩余容量之和不小于 p。如果有多个疏散区域到事故区域的最短路径长度相同，则优先选择编号较小的区域。

输入格式

第一行包含一个正整数 n，表示区域的数量。

接下来 n行，每行包含 n个整数，表示矩阵 dist。

接下来一行包含 n 个整数，表示每个区域的剩余容量 cap[i]。

最后两行包含两个整数 x 和 p，分别表示发生事故的区域编号和需要疏散的人数。

输出描述

输出一行，包含若干个整数，表示选择的疏散区域编号。如果有多个疏散区域到事故区域的最短路径长度相同，则按照编号从小到大的顺序输出。

样例

输入

4
-1 5 -1 8
5 -1 1 3
-1 1 -1 4
8 3 4 -1
10 20 15 25
2
12

输出

1

其实就是一个无向图：

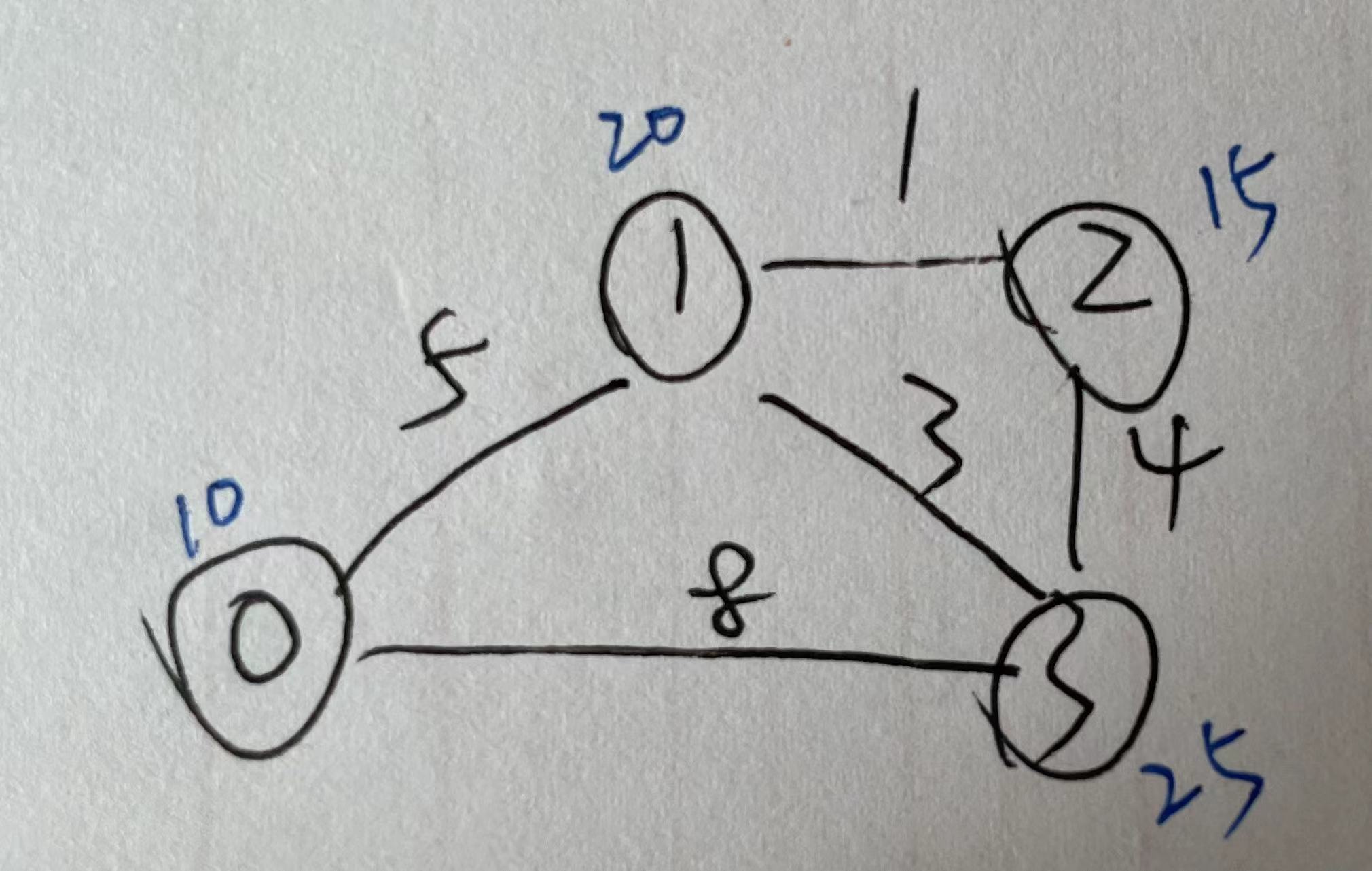
数据范围

• $2\le n\le 10^4$
• $-1\le dist[i][j]\le 1000$
• $1\le cap[i]\le 100$
• $0\le x<n$
• $0<p\le 1000$

OJ链接：
https://codefun2000.com/p/P1829

解题思路一：Dijkstra

本题可以使用 Dijkstra 算法求出事故区域到其他所有区域的最短路径长度，然后将区域按照最短路径长度从小到大排序，依次选择区域作为疏散目的地，直到选择的区域剩余容量之和不小于需要疏散的人数为止。

具体步骤如下：

1. 使用 Dijkstra 算法求出事故区域到其他所有区域的最短路径长度，记为 d[i]。
2. 将区域按照 (d[i], i, cap[i]) 的顺序从小到大排序，其中 d[i] 为最短路径长度，cap[i] 为剩余容量，i 为区域编号。
3. 依次选择排序后的区域作为疏散目的地，直到选择的区域剩余容量之和不小于需要疏散的人数为止。
4. 输出选择的疏散区域编号。

import heapq

n = int(input())
dist = [list(map(int, input().split())) for _ in range(n)]
cap = list(map(int, input().split()))
x = int(input())
p = int(input())

for i in range(n):
    for j in range(n):
        if dist[i][j] == -1:
            dist[i][j] = float('inf')

d = [float('inf')] * n
d[x] = 0
q = [(0, x)]

while q:
    _, u = heapq.heappop(q)
    for v in range(n):
        if d[u] + dist[u][v] < d[v]:
            d[v] = d[u] + dist[u][v]
            heapq.heappush(q, (d[v], v))

regions = sorted([(d[i], i, cap[i]) for i in range(n) if i != x])

ans = []
total_cap = 0
for _, i, c in regions:
    if total_cap >= p:
        break
    ans.append(i)
    total_cap += c
print(*ans)

时间复杂度：O(n²)其中 n 为区域的数量。
空间复杂度：O(n²)

解题思路二：0

时间复杂度：O(n²)其中 n 为区域的数量。
空间复杂度：O(n²)

解题思路三：java, c++

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int[][] dist = new int[n][n];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                dist[i][j] = sc.nextInt();
                if (dist[i][j] == -1) {
                    dist[i][j] = Integer.MAX_VALUE;
                }
            }
        }
        int[] cap = new int[n];
        for (int i = 0; i < n; i++) {
            cap[i] = sc.nextInt();
        }
        int x = sc.nextInt();
        int p = sc.nextInt();

        int[] d = new int[n];
        Arrays.fill(d, Integer.MAX_VALUE);
        d[x] = 0;
        PriorityQueue<int[]> q = new PriorityQueue<>((a, b) -> a[0] - b[0]);
        q.offer(new int[]{0, x});

        while (!q.isEmpty()) {
            int[] curr = q.poll();
            int u = curr[1];
            for (int v = 0; v < n; v++) {
                if (d[u] + dist[u][v] < d[v]) {
                    d[v] = d[u] + dist[u][v];
                    q.offer(new int[]{d[v], v});
                }
            }
        }

        List<int[]> regions = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            if (i != x) {
                regions.add(new int[]{d[i], i, cap[i]});
            }
        }
        regions.sort((a, b) -> {
            if (a[0] != b[0]) {
                return a[0] - b[0];
            }
            if (a[1] != b[1]) {
                return b[1] - a[1];
            }
            return a[2] - b[2];
        });

        List<Integer> ans = new ArrayList<>();
        int totalCap = 0;
        for (int[] region : regions) {
            if (totalCap >= p) {
                break;
            }
            ans.add(region[1]);
            totalCap += region[2];
        }

        for (int i = 0; i < ans.size(); i++) {
            System.out.print(ans.get(i));
            if (i < ans.size() - 1) {
                System.out.print(" ");
            }
        }
    }
}

#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;

const int INF = 0x3f3f3f3f;

int main() {
    int n;
    cin >> n;
    vector<vector<int>> dist(n, vector<int>(n));
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            cin >> dist[i][j];
            if (dist[i][j] == -1) {
                dist[i][j] = INF;
            }
        }
    }
    vector<int> cap(n);
    for (int i = 0; i < n; i++) {
        cin >> cap[i];
    }
    int x, p;
    cin >> x >> p;

    vector<int> d(n, INF);
    d[x] = 0;
    priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q;
    q.emplace(0, x);

    while (!q.empty()) {
        auto [du, u] = q.top();
        q.pop();
        if (du > d[u]) {
            continue;
        }
        for (int v = 0; v < n; v++) {
            if (d[u] + dist[u][v] < d[v]) {
                d[v] = d[u] + dist[u][v];
                q.emplace(d[v], v);
            }
        }
    }

    vector<tuple<int, int, int>> regions;
    for (int i = 0; i < n; i++) {
        if (i != x) {
            regions.emplace_back(d[i], i, cap[i]);
        }
    }
    sort(regions.begin(), regions.end());

    vector<int> ans;
    int total_cap = 0;
    for (auto [di, i, ci] : regions) {
        if (total_cap >= p) {
            break;
        }
        ans.push_back(i);
        total_cap += ci;
    }

    for (int i = 0; i < ans.size(); i++) {
        cout << ans[i];
        if (i < ans.size() - 1) {
            cout << " ";
        }
    }
    cout << endl;

    return 0;
}

时间复杂度：O(n²)其中 n 为区域的数量。
空间复杂度：O(n²)

---

创作不易，观众老爷们请留步… 动起可爱的小手，点个赞再走呗 (๑◕ܫ￩๑) 欢迎大家关注笔者，你的关注是我持续更博的最大动力

原创文章，转载告知，盗版必究

---

---

---

♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠