要想知道矩阵快速幂,我们先了解一下什么叫快速幂和矩阵乘法
一、快速幂
快速幂算法是用来快速计算指数表达式的值的,例如 210000000,普通的计算方法 2*2*2*2…10000000次,如果一个数字的计算都要计算那么多次的话,那么这个程序一定是失败的。
快速幂思想及实现
快速幂思想其实很简单,就是公式的转换
1、当指数是偶数时,我们可以让指数除以2,底数乘以底数
2、当指数是奇数时,我们可以将指数变为偶数
#include <iostream>
using namespace std;
typedef long long LL;
long long fpow(long long x, long long p)
{
long long ans = 1;
//完整代码
//while (p) {
// if (p % 2 == 1) {
// ans *= x, p--;
// }
// else {
// p /= 2;
// x *= x;
// }
//}
//精简代码
while (p) {
if (p & 1) ans *= x ; //p为奇数
p >>= 1;
x *=x;
}
return ans;
}
int main()
{
LL x, p;
cin >> x >> p;
cout << fpow(x, p) << endl;
}二、矩阵乘法
图文演示:

#include <iostream>
#include <algorithm>
using namespace std;
typedef long long int ll;
const int mod = (int)1e9 + 7;
const int N = 1e3;
int a[N][N], b[N][N];
int temp[N][N];
// a = a * b
void MAXMP(int a[][N], int b[][N], int n, int p, int m) //第一个矩阵的行,两个矩阵相同的列行,第二个矩阵的列,
{
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++) temp[i][j] = 0;
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
for (int k = 1; k <= p; k++)
{
temp[i][j] = (temp[i][j] + (a[i][k] * b[k][j]) % mod) % mod;
}
}
}
}
int main()
{
int n, m, p;
cin >> n >> p >> m; //行 列行 列
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= p; j++) cin >> a[i][j];
}
for (int i = 1; i <= p; i++)
{
for (int j = 1; j <= m; j++) cin >> b[i][j];
}
MAXMP(a, b, n, p, m);
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++) cout << temp[i][j] << endl;
}
}三、矩阵快速幂
矩阵快速幂,即给定一个矩阵),快速计算
。一般来说,矩阵快速幂只会涉及方阵即
,所以下面以方阵为例。(一般来说,只有方阵存在矩阵幂值,故此时等行等列)
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long int ll;
const int mod = (int)1e9 + 7;
const int N = 1e3;
int a[N][N], res[N][N];
int temp[N][N];
// a = a * b
void MXMP(int a[][N], int b[][N], int n)
{
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++) temp[i][j] = 0;
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
for (int k = 1; k <= n; k++)
{
temp[i][j] = (temp[i][j] + (a[i][k] * b[k][j]) % mod) % mod;
}
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) a[i][j] = temp[i][j];
}
}
void PowerMod(int a[][N], int n, int x)//x为次幂,n为矩阵行,m为矩阵行
{
memset(res, 0, sizeof(res));
for (int i = 1; i <= n; i++) res[i][i] = 1;//初始化为单位矩阵
while (x){
if (x & 1) MXMP(res, a, n);
MXMP(a, a, n);
x >>= 1;
}
}
int main()
{
int n, x;
cin >> n >> x;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++) cin >> a[i][j];
}
PowerMod(a, n, x);
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++) cout << res[i][j] <<" ";
cout << endl;
}
return 0;
}四、矩阵快速幂的应用
斐波拉契函数
例如:斐波那契数列的递推计算的时间复杂度为O ( n ),,换成矩阵乘法的形式,即
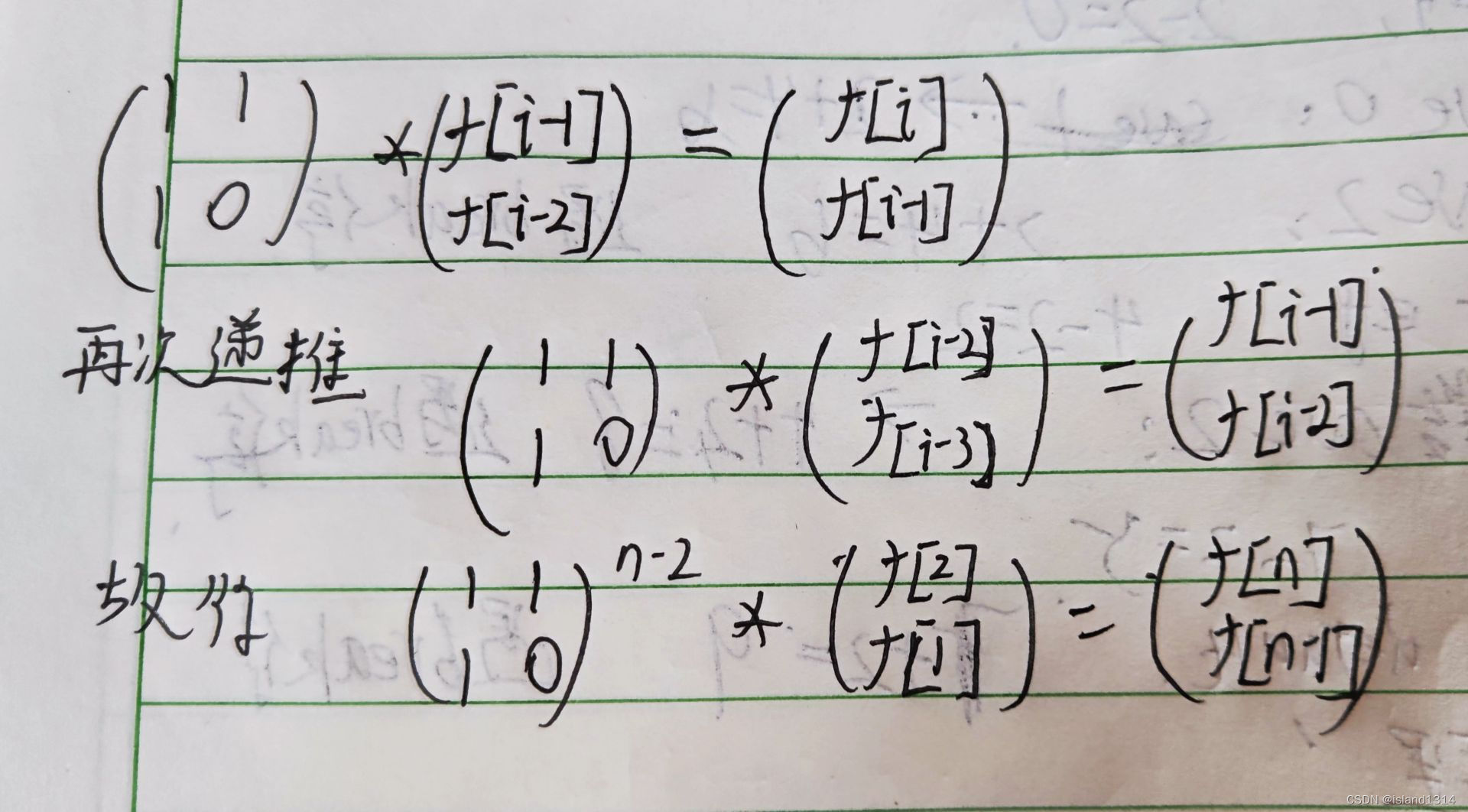
利用矩阵乘法和快速幂运算,时间复杂度可达到 O(2^3\ logn)O优于普通的O(n), 其中数字2 为抽象出的矩阵边长 2^32 为矩阵乘法运算的时间,logn为快速幂运算时间。
注意:实现时为了简便可以把矩阵C的大小设置成等同于矩阵B的大小,空位用0填充
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long int ll;
const int mod = (int)1e9 + 7;
const int N = 1e3;
int a[N][N], res[N][N];
int temp[N][N];
int f[N][N];
// a = a * b
void MXMP(int a[][N], int b[][N], int n)
{
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++) temp[i][j] = 0;
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
for (int k = 1; k <= n; k++)
{
temp[i][j] = (temp[i][j] + (a[i][k] * b[k][j]) % mod) % mod;
}
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) a[i][j] = temp[i][j];
}
}
void PowerMod(int a[][N], int n, int x)//x为次幂,n为矩阵行列
{
memset(res, 0, sizeof(res));
for (int i = 1; i <= n; i++) res[i][i] = 1;//初始化为单位矩阵
while (x){
if (x & 1) MXMP(res, a, n);
MXMP(a, a, n);
x >>= 1;
}
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
a[i][j] = res[i][j];
}
int solve(int n)
{
if (n == 1 || n == 2) return 1;
a[1][1] = 1, a[1][2] = 1;
a[2][1] = 1, a[2][2] = 0;
PowerMod(a, 2, n - 2);
f[1][1] = 1, f[2][1] = 1;
MXMP(a, f, 2);
return a[1][1];
}
int main()
{
int n;
cin >> n;
cout << solve(n) << endl;
return 0;
}