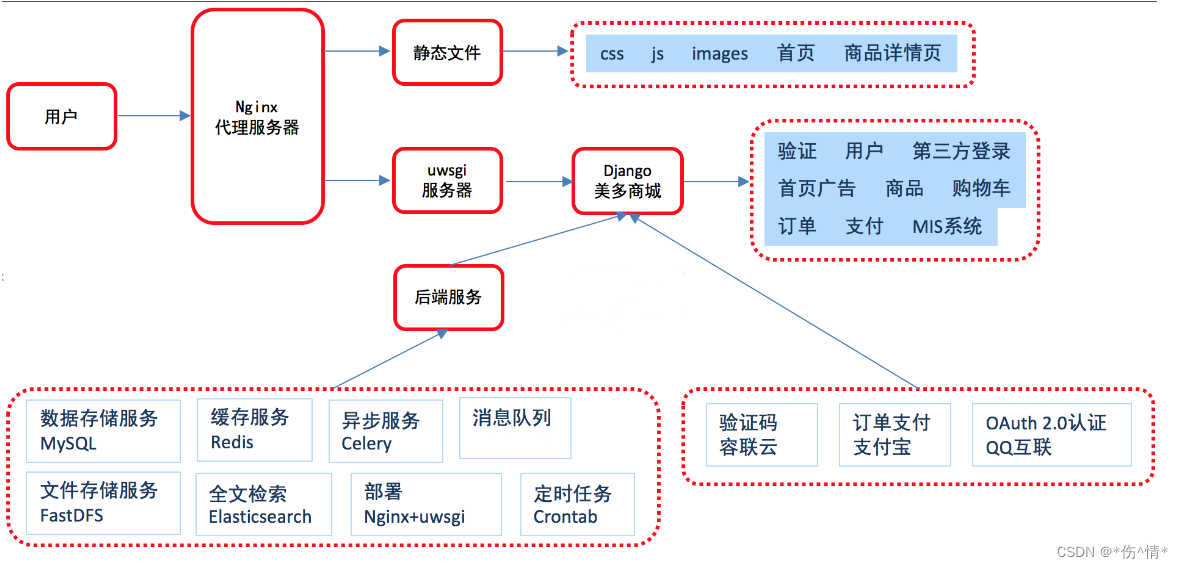
一、算法设计与分析的基本概念
1.1算法
算法(Algorithm)是对特定问题求解步骤的一种描述,有5个重要特性:
·有穷性:一个算法必须总是在执行又穷步骤后结束,且每一步都可在又穷时间内完成
·确定性算法中每一条指令必须有确切的含义,理解时不会产生二义性,并且在任何条件下,算法只有唯一的一条执行路径,即对于相同的输入只能得到相同的输出
·可行性:一个算法是可行的,即算法中的描述操作都可以通过已经实现的基本运算执行有限次来执行
·输入:一个算法有零个或多个输入,这些输入取自于某个特定的对象集合
·输出:一个算法有一个或多个输出,这些输出是同输入有某些特定关系的量
算法设计:包括正确性、可读性、健壮性和高效性等
1.2算法的表示
常用算法表示有自然语言、流程图、程序设计语言和伪代码等
·自然语言:容易理解,但容易出现二义性,且算法代码很冗长
·流程图:直观易懂,但严密性不如程序设计语言,灵活性不如自然语言
·程序设计语言:能用计算机直接执行,但抽象性差
·伪代码:介于自然语言和程序设计语言之间,具有很强表达力
下午题不仅考察算法设计和分析技术,同时还考核C语言或java语言实现
二、算法分析基础
2.1时间复杂度
根据输入的不同,将算法的时间复杂度分为三种情况:
·最佳情况:使算法执行时间最少的输入
·最坏情况:使算法执行时间最多的输入。一般会进行算法在最坏时间复杂度的分析,因为最坏情况是在任何输入下运行时间的一个上限
·平均情况:算法的平均运行时间
2.2渐进符号

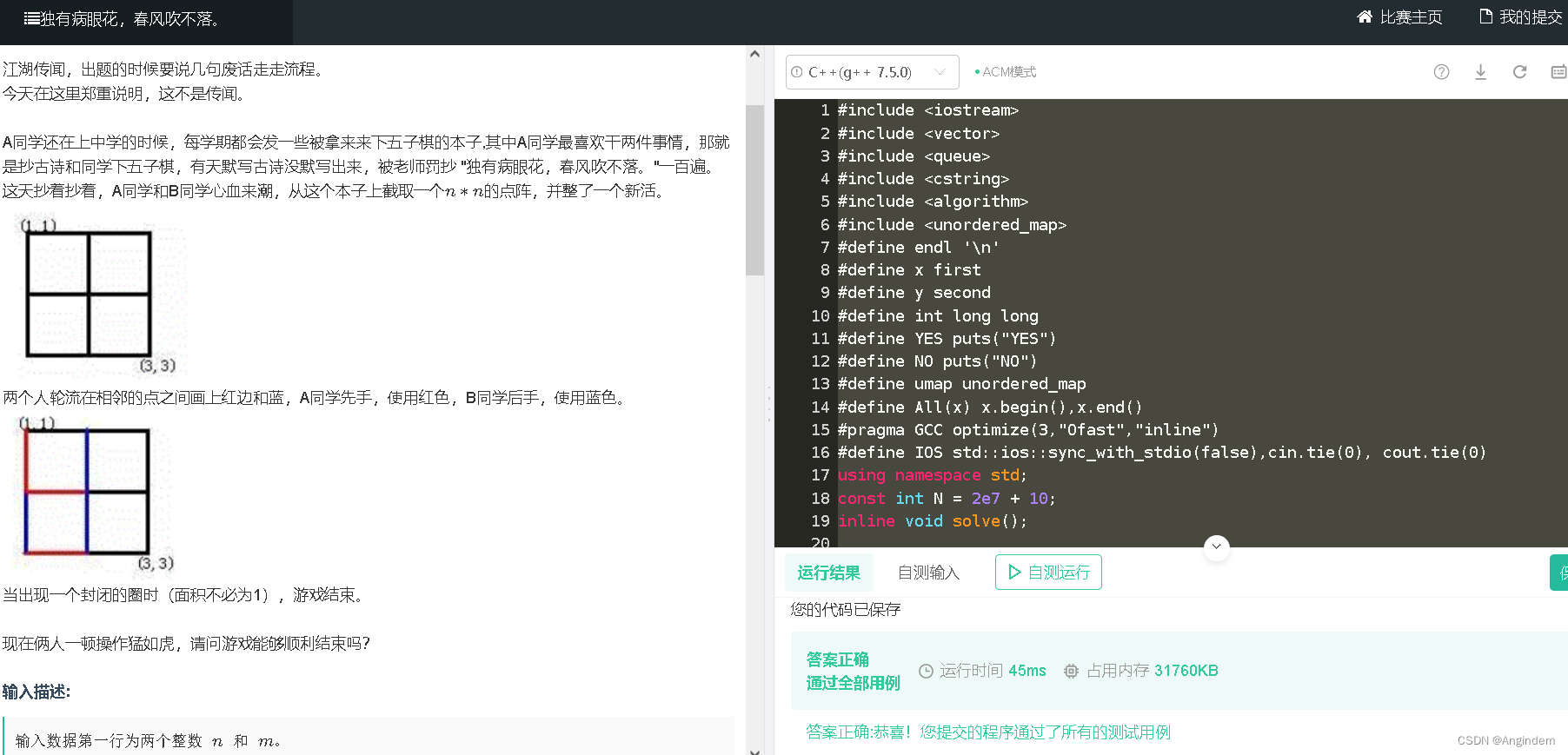
2.3递归式
从算法结构上来看,算法可分为非递归形式和递归形式。非递归算法的时间复杂度分析比较简单,本节主要讨论递归算法的时间复杂度分析方法
·展开法:将递归式中右边的项根据递归式进行替换,称为展开,如此下去,一直得到一个一个求和表达式,得到结果
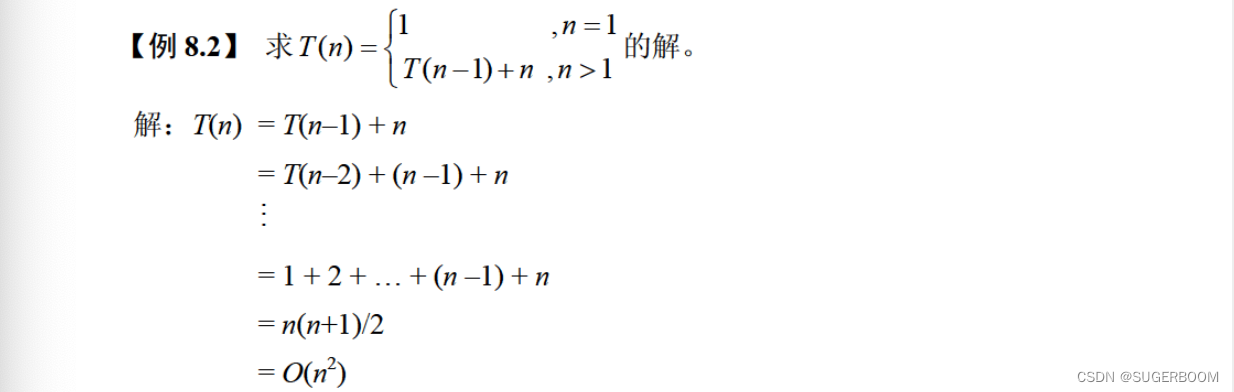
·代换法:当归纳假设用较小的值时,用所猜测的值代替函数的解

2.4算法的复杂度
常数级:代码中没有循环 O(1)
线性级:一重循环 for(i = 0; i < n; i++) O(n)
对数级:出现“乘” while(count < n){...} O(lg n)
平方级:多重循环 for( ){for( ){...}...} O(n^m)
三、分治法
3.1递归的概念
递归指子程序或函数直接或间接调用自己,是一种描述问题 和解决问题的常用方法
3.2分治法基本思想
将一个问题分解为多个小问题,分界处的子问题一般相同,相互独立
分解、求解、合并
3.3分治法实例
1)归并排序
分解:将n个元素分解成各含n/2个元素的子序列
求解:用归并排序对两个子序列递归的排序
合并:合并两个已经排序好的子序列已得到排序结果
import java.util.Arrays;
public class MergeSort {
public static void main(String[] args) {
int[] nums = {-1, 2, -8, -10}; //给定一个数组
int[] after = sortArray(nums); //的带排序后的数组
System.out.println(Arrays.toString(after)); //打印输出得到数组
}
private static int[] sortArray(int[] nums) {
int len = nums.length;
int[] temp = new int[len];
mergeSort(nums,0,len-1,temp);
return nums;
}
/**
* 递归函数对nums[left...right]进行归并排序
* @param nums 原数组
* @param left 左边的索引
* @param right 右边记录索引位置
* @param temp
*/
private static void mergeSort(int[] nums, int left, int right, int[] temp) {
if (left == right){//当拆分到数组当中只要一个值的时候,结束递归
return;
}
int mid = (left+right)/2; //找到下次要拆分的中间值
mergeSort(nums,left,mid,temp);//记录树左边的
mergeSort(nums,mid+1,right,temp);//记录树右边的
//合并两个区间
for (int i = left; i <= right; i++) {
temp[i] = nums[i];
//temp就是辅助列表,新列表的需要排序的值就是从辅助列表中拿到的
}
int i = left; //给辅助数组里面的值标点
int j = mid +1;
for (int k = left; k <= right ; k++) {//k 就为当前要插入的位置
if (i == mid + 1){
nums[k] = temp[j];
j++;
}else if (j == right+1){
nums[k] = temp[i];
i++;
}
else if (temp[i] <= temp[j]){
nums[k] = temp[i];
i++;
}else {
nums[k] = temp[j];
j++;
}
}
}
}
四、动态规划法
4.1动态规划法基本思想
同样是将求解问题分解成若干个子问题,但分解出的子问题不一定相同,独立。
动态规划法适用于求全局最优解
步骤:1)找出最优解的性质,并刻画其结构性质;2)递归的定义最优解的值;3)以自底向上的方式计算出最优解;4)根据计算最优解
4.2动态规划法典型实例
0-1背包问题:

·刻画0-1背包问题的最优解结构:
将背包问题的求解看作是进行一系列决策的过程,即决定哪些物品应该放入,哪些不该放入。如果一个问题的最优解包含了物品n,即Xn=1,那么其余的X1,X2……Xn-1一定构成子问题1,2……(n-1)在容量为W-wn时的最优解。如果这个最优解不包含物品n,即Xn=0,那么其余的一定构成子问题在容量为W时的最优解
·递归定义最优解的值:

·计算背包问题最优解的值
import java.util.Scanner;
public class Knapsack {
private static int n;//表示有多少个物品
private static int c;//容量
private static int d;//容积
private static int[] weightArr;
private static int[] volumeArr;
private static int[] valueArr;
private static int[][][] dp;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.print("请输入物品个数:");
n = sc.nextInt();
System.out.print("请输入背包容量:");
c = sc.nextInt();
System.out.print("请输入背包容积:");
d = sc.nextInt();
weightArr = new int[n + 1];
volumeArr = new int[n + 1];
valueArr = new int[n + 1];
dp = new int[n + 1][c + 1][d + 1];//dp[i][j][k]i代表着第1到第i个物品,j代表的是重量,k代表的是容积,dp为最优价值
System.out.println("请分别输入物品重量:");
for (int i = 1; i <= n; i++) {
weightArr[i] = sc.nextInt();
}
System.out.println("请分别输入物品体积:");
for (int i = 1; i <= n; i++) {
volumeArr[i] = sc.nextInt();
}
System.out.println("请分别输入物品价值:");
for (int i = 1; i <= n; i++) {
valueArr[i] = sc.nextInt();
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= c; j++) {
for (int k = 1; k <= d; k++) {
if (j >= weightArr[i] && k >= volumeArr[i]) {
dp[i][j][k] = Math.max(dp[i - 1][j][k], dp[i - 1][j - weightArr[i]][k - volumeArr[i]] + valueArr[i]);
} else {
dp[i][j][k] = dp[i - 1][j][k];
}
}
}
}
System.out.println("最大总价值是:" + dp[n][c][d]);
int x[] = new int[99]; //记录是否被选中
for (int i = n; i > 1; i--)
if (dp[i][c][d] == dp[i - 1][c][d]) {
x[i] = 0;
} else {
x[i] = 1;
c -= weightArr[i];
d -= volumeArr[i];
}
x[1] = (dp[1][c][d] != 0) ? 1 : 0;
System.out.println("被选入背包的物品的编号,质量和体积,价值分别是:");
for (int i = 1; i < n + 1; i++)
if (x[i] == 1)
System.out.println("第" + i + "个物品:" + weightArr[i] + " " + volumeArr[i] + " " + valueArr[i]);
}
}
上述代码时间复杂度为O(nW),最优解的值为24

五、贪心法
5.1贪心法的基本思想
贪心法是一种简单的算法,和动态规划法一样,贪心法也常用于求解最优化问题。与动态规划法不同的是,贪心法在解决问题的策略上是仅根据当前已有的信息做出判断,而且一旦做出了选择,不管将来有什么结果,这个选择都不会改变。换言之,贪心法并不是从整体最优考虑,他所做出的选择只是局部最优解。
5.2贪心法的典型实例
·背包问题:


package 贪心算法解决背包问题;
import java.util.Scanner;
public class Value {
public static Scanner scanner = new Scanner(System.in);
public static int n;// 物品个数
public static float C;// 背包容量
public static float[] weight;// 重量数组
public static float[] value;// 价值数组
// 拷贝的目的是,在后面对重量数组和价值数组进行了排序,打乱了原来的数组顺序,故先拷贝出来一份。
public static float[] v;// 拷贝一份价值数组
public static float[] w;// 拷贝一份重量数组
public static float[] add;// 放入的比例数组
public static void main(String[] args) {
// TODO Auto-generated method stub
System.out.print("请输入物品的个数:");
n = scanner.nextInt();
weight = new float[n];
value = new float[n];
v = new float[n];
w = new float[n];
System.out.print("请输入背包的容量:");
C = scanner.nextFloat();
System.out.println("请输入物品的重量和价值:");
for (int i = 0; i < n; i++) {
weight[i] = scanner.nextFloat();
value[i] = scanner.nextFloat();
// 进行拷贝
v[i] = value[i];
w[i] = weight[i];
}
addBag();
float total = totalValue();
System.out.println("背包的总价值为:" + total);
}
/**
* @see 计算总价值
* @return 返回总价值
*/
public static float totalValue() {
float total = 0;
for (int i = 0; i < n; i++) {
total += add[i] * value[i];
}
return total;
}
/**
* @see 计算物品放入的比例,放入到add数组中
*/
public static void addBag() {
add = new float[n];
// 给价值数组进行排序,价值大的在前面
int index[] = Arraysort(value);// 对value进行了排序
for (int i = 0; i < n; i++) {
if (w[index[i]] <= C) {
// 加入背包中
add[index[i]] = 1;
C = C - w[index[i]];
} else {
// 按比例加入背包中
add[index[i]] = C / w[index[i]];
}
}
System.out.print("放入重量比例:");
for (float i : add) {
System.out.print("\t" + i);
}
System.out.println();
System.out.print("单个物品价值:");
for (float i : value) {
System.out.print("\t" + i);
}
System.out.println();
}
/**
* @see 将传进来的数组进行排序,小的在前面
* @param arr
* @return 返回原来数组的下标
*/
public static int[] Arraysort(float[] arr) {
float temp;
int index;
int k = arr.length;
int[] Index = new int[k];
for (int i = 0; i < k; i++) {
Index[i] = i;
}
for (int i = 0; i < arr.length; i++) {
for (int j = 0; j < arr.length - i - 1; j++) {
if (arr[j] < arr[j + 1]) {
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
index = Index[j];
Index[j] = Index[j + 1];
Index[j + 1] = index;
}
}
}
return Index;
}
}
package 贪心算法解决背包问题;
import java.util.Scanner;
public class Weight {
public static Scanner scanner = new Scanner(System.in);
public static int n;// 物品个数
public static float C;// 背包容量
public static float[] weight;// 重量数组
public static float[] value;// 价值数组
// 拷贝的目的是,在后面对重量数组和价值数组进行了排序,打乱了原来的数组顺序,故先拷贝出来一份。
public static float[] v;// 拷贝一份价值数组
public static float[] w;// 拷贝一份重量数组
public static float[] add;// 放入的比例数组
public static void main(String[] args) {
// TODO Auto-generated method stub
System.out.print("请输入物品的个数:");
n = scanner.nextInt();
weight = new float[n];
value = new float[n];
v = new float[n];
w = new float[n];
System.out.print("请输入背包的容量:");
C = scanner.nextFloat();
System.out.println("请输入物品的重量和价值:");
for (int i = 0; i < n; i++) {
weight[i] = scanner.nextFloat();
value[i] = scanner.nextFloat();
// 进行拷贝
v[i] = value[i];
w[i] = weight[i];
}
addBag();
float total = totalValue();
System.out.println("背包的总价值为:" + total);
}
/**
* @see 计算总价值
* @return 返回总价值
*/
public static float totalValue() {
float total = 0;
for (int i = 0; i < n; i++) {
total += add[i] * value[i];
}
return total;
}
/**
* @see 计算物品放入的比例,放入到add数组中
*/
public static void addBag() {
add = new float[n];
// 给重量数组进行排序,重量小的在前面
int index[] = Arraysort(weight);// 对weight进行了排序
for (int i = 0; i < n; i++) {
if (w[index[i]] <= C) {
// 加入背包中
add[index[i]] = 1;
C = C - w[index[i]];
} else {
// 按比例加入背包中
add[index[i]] = C / w[index[i]];
}
}
System.out.print("放入重量比例:");
for (float i : add) {
System.out.print(i + "\t");
}
System.out.println();
System.out.print("单个物品价值:");
for (float i : value) {
System.out.print(i + "\t");
}
System.out.println();
}
/**
* @see 将传进来的数组进行排序,小的在前面
* @param arr
* @return 返回原来数组的下标
*/
public static int[] Arraysort(float[] arr) {
float temp;
int index;
int k = arr.length;
int[] Index = new int[k];
for (int i = 0; i < k; i++) {
Index[i] = i;
}
for (int i = 0; i < arr.length; i++) {
for (int j = 0; j < arr.length - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
index = Index[j];
Index[j] = Index[j + 1];
Index[j + 1] = index;
}
}
}
return Index;
}
}
package 贪心算法解决背包问题;
import java.util.Scanner;
public class Density {
public static float C1 = 0;// 总价值
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner scanner = new Scanner(System.in);
System.out.print("请输入物品的个数:");
int n = scanner.nextInt();
System.out.print("请输入背包的容量:");
float C = scanner.nextFloat();
System.out.println("请输入物品的重量和价值:");
float[] wi = new float[n + 2];
float[] vi = new float[n + 2];
float[] x = new float[n + 2];
float[] v2 = new float[n + 1];
float[] w2 = new float[n + 1];
for (int i = 1; i <= n; i++) {
wi[i] = scanner.nextFloat();
vi[i] = scanner.nextFloat();
v2[i] = vi[i];
w2[i] = wi[i];
}
Density test = new Density();
test.Knapsack(n, C, vi, wi, x, v2, w2);
System.out.println();
System.out.print("单个物品价值:");
for (int i = 1; i <= n; i++) {
System.out.print("\t" + v2[i]);
}
System.out.println();
System.out.println("背包的总价值为:" + C1);
}
/**
* @see 将物品按价值比从大到小排放在数组
* @param n 物品个数
* @param v 价值数组
* @param w 重量数组
*/
void Sort(int n, float[] v, float w[]) {
float temp1;
float temp2;
for (int i = 1; i <= n; i++) {
for (int s = 1; s <= i; s++) {
if (v[i] / w[i] > v[s] / w[s]) {
temp1 = v[s];
temp2 = w[s];
v[s] = v[i];
w[s] = w[i];
v[i] = temp1;
w[i] = temp2;
}
}
}
}
void Knapsack(int n, float W, float v[], float w[], float x[], float v2[], float w2[]) {
Density a = new Density();
a.Sort(n, v, w);
int i;
for (i = 1; i <= n; i++)
x[i] = 0;
float c = 0;
for (i = 1; i <= n; i++) {
if (w[i] > W)
break;// 如果物品的重量大于背包剩余容量,停止放入整个物品
for (int t = 1; t <= n; t++) {
if (w[i] == w2[t] && v[i] == v2[t])// 将放入了的物品标记为1
x[t] = 1;
}
W -= w[i];
c += v[i];
}
if (i <= n) {
for (int q = 1; q <= n; q++) {
if (w[i] == w2[q] && v[i] == v2[q]) {
x[q] = W / w[i];// 放入部分物品记录放入的比例
c += x[q] * v[i];
}
}
}
System.out.print("放入重量比例:");
for (int k = 1; k <= n; k++) {
System.out.print("\t" + x[k]);
}
C1 = c;
}
}
六、回朔法
6.1回朔法的算法框架
在应用回朔法解决问题时,首先应明确定义问题的解空间。问题的解空间应该=至少包含问题的一个(最优)解。例如,有n种可选择物品的0-1背包问题。定义了问题的解空间后,还应将解空间很好的组织起来,使回朔法能方便的搜索整个空间。例如对于n=3的0-1背包问题:
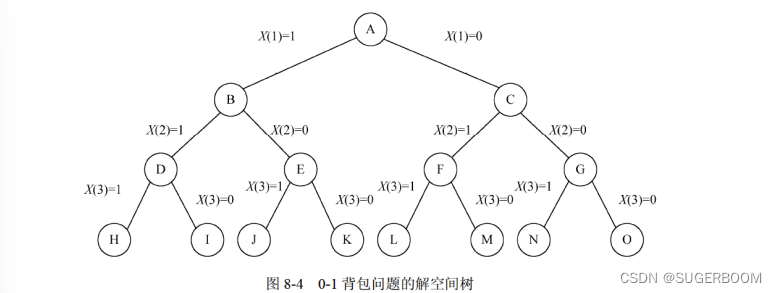
6.2回朔法的基本思想
在确定了解空间的组织结构后,回朔法从开始节点出发,以深度优先的方式搜索整个空间。回朔法不停的以递归的方式在解空间中搜索,直到找到所要求的解或空间中已无活结点为止
一般用于解决迷宫类问题,深度优先,搜索空间树
6.3回朔法的典型实例
八皇后问题:
public class Tools {
private static int count = 1;//计数,统计总共有多少种方法
/**
* 一维数组解决八皇后问题
* @param n 第1行的第n列
* @param map 棋盘
* @param max 棋盘大小为 max * max
*/
public static void check(int n, int[] map, int max) {
//如果n已经在第max个位置,则说明已经找完,直接退出
if(n == max) {
System.out.println("第" + (count++) + "种");
print(map);
return;//退出 check方法
}
//依次放置皇后,并判断是否有冲突
for (int i = 0; i < max; i++) {
//先把当前这个皇后n 放到该行的第一列
map[n] = i;
//判断当放置第n个皇后到i列时,是否冲突
if(judge(n, map)) {//不冲突
check(n + 1, map, max);
}
//如果冲突,就继续执行 array[n] = i,即:将第n个皇后,放置在本行的后移一个位置
}
}
//查看当我们放置第n个皇后,就去检测该皇后是否和前面已经摆放的皇后冲突
private static boolean judge(int n, int[] map) {
for (int i = 0; i < n; i++) {
//1. array[n] == array[i] 表示判断 第n个皇后是否和前面的 n-1个皇后在同一列
//2. Math.abs(n - i) == Math.abs(map[n] - map[i]) 表示判断 第n个皇后是否和 第i个皇后在同一斜线
if(map[n] ==map[i] || Math.abs(n - i) == Math.abs(map[n] - map[i]) ) {
return false;
}
}
return true;
}
/**
* 把存放在 array数组中的摆放方法输出
* @param map 棋盘
*/
private static void print(int[] map) {
//遍历 array数组
for (int i = 0; i < map.length; i++) {
System.out.print(map[i] + " ");
}
System.out.println();//换行
}
}
public class Test {
public static void main(String[] args) {
int[] map = new int[8];//定义一个长度为 8的一维数组
Tools.check(0, map, 8);
}
}
七、其他算法
软考中级主要考察:分治法、动态规划法、贪心法、回朔法
其他算法了解即可,此处仅简单了解
概率算法:在算法执行某些步骤时,随机选择下一步如何进行,允许结果以较小概率出现错误,获得算法运行时间大幅减少(降低复杂度)
数据挖掘算法:分析爆炸式增长的各类数据的技术(分类、回归、关联规则)功能
智能优化算法:求解各类工程问题优化解的应用技术(人工神经网络ANN、遗传算法、模拟退火算法SA、蚁群算法……)
分支界限法:类似于回朔法,但一般情况下与回朔法的求解目标不同。分支界限法的目标是找出满足约束条件的一个解,即在某种意义下的最优解