参考资料
1·.《基于遗传算法（deap库）的一元函数寻优代码详解》
2.官方文档:http://deap.readthedocs.io/en/master/index.html
3.《 Deap: python中的遗传算法工具箱》 ，⭐️666

——————

壹、overview

一、Types

使用创建器creator 创建类型并使用工具箱初始化类型。一般代码格式为：

from deap import creator # 导入创建器
creator.create() #创建格式

栗子

from deap import bass #导入基类
creator.create("FitnessMin", base.Fitness, weights=(-1.0,)) # 创建适应度

creator.create("Individual", list, fitness=creator.FitnessMax)#创建个体

注意：
该create()函数至少接受两个参数，一个新创建的类的名称和一个基类。任何后续参数都将成为类的属性。

1. Fitness 适应度

Fitness 是一个抽象类，它位于base之下，一般说明创建的类使用base.Fitness.需要属性weights. weights 该属性必须为元组，以便以相同的方式处理多目标和单目标适应度

此代码生成一个适应度，该适应度最小化第一个目标并最大化第二个目标。权重还可用于改变每个目标的重要性。这意味着权重可以是任何实数，并且仅使用符号来确定是否进行了最大化或最小化。权重有用的一个例子是在 NSGA-II 选择算法中进行的拥挤距离排序。

1.1 单目标和多目标

creator.create("FitnessMin", base.Fitness, weights=(-1.0,)) # 单目标，最小化

creator.create("FitnessMulti", base.Fitness, weights=(-1.0, 1.0))# 双目标，第一个最小化，第二个最大化

两个目标，权重属性的个数为2.由二元组表示。

• 1 表示目标最大化；
• -1 表示目标最小化；
• 必须由 元组 构成

2、 Individual 个体

不同的进化算法（GA、GP、ES、PSO、DE、…）有不同风格。对于个体，我们使用了Toolbox的初始化方法。

from deap import tools

对于个体的搭建完成，前提工作需要两个：

1. 确定个体组装样式，比如以列表(List)的形式排排坐 ，或者以树(tree)的形式。可以理解为包装盒是方的还是圆的—creator.creat()创造
2. 确定个体的特性，比如随机浮点数、排列等。比如装水果的箱子记作A箱，装电器的箱子记作B箱。这些箱子即起了名字，又固定使用属性—toolbox.register()注册

2.1 List of Floats 浮点数列表

⭐️创建create

创建一个个体Individual类, 该类的标准是列表List的形式，且应该服从适应度(fitss)的属性。

栗子

import random

from deap import base
from deap import creator
from deap import tools

creator.create("FitnessMax", base.Fitness, weights=(1.0,))
creator.create("Individual", list, fitness=creator.FitnessMax)

这里值得提醒的是：

• 第一个适应度函数的名和个体中服从的适应度函数名，应该是一致的。
• 适应度函数的名字可以不为”FitnessMax",可以随便取一个“Fitnessmaxfun",但注意要前后一致。

⭐️注册register

IND_SIZE=10

toolbox = base.Toolbox()
toolbox.register("attr_float", random.random)
#将随机函数 注册为别名 "att_float",表示浮点数属性

toolbox.register("individual", tools.initRepeat, 
creator.Individual, #参数，返回的数据类型
toolbox.attr_float,#参数，函数
n=IND_SIZE) #参数，重复次数-》基因

新引入register()的方法至少需要两个参数;别名和分配给此别名的函数。

• 第一个重定向到该 random.random() 函数。
• 第二个是 initRepeat() 函数的快捷方式，将其 container 参数固定到 creator.Individual 类，将其 func 参数固定到 toolbox.attr_float() 函数，将其重复次数参数固定到 IND_SIZE 。

✋小课堂

initRepeat(container, func, n)
Call the function func n times and return the results in a container type container. 调用函数’fuc’ 有‘n’次，并将返回的结果放入容器container中。

• 参数container：func导出的数据类型
• 参数 func: 将被调用n次以填充容器的函数
• 参数n:重复调用的次数

🐒 解析

1. individual是别名；
2. tools.initRepeat是重复函数，后面3个参数是它的参数；
3. 注册individual的含义为：调用浮点类型的随机函数(别名为toolbox.attr_float),调用10次(变量为IND_SIZE),返回的结果放入个体creator.Individual(该个体是List的形式，且与适应度FitnessMax绑定了)
4. toolbox.individual和creator.Individual两者不同，前者继承了后者。
5. 调用 toolbox.individual() 将使用固定参数进行调用 initRepeat() ，并返回一个由IND_SIZE浮点数组成的完整 creator.Individual 值，并具有最大化的单个目标 fitness 属性。

2.2 list类型的变体

通过继承或 array.array或者 numpy.ndarray 如下方式，可以进行此类型的变体。
⭐️ array.array

import  array
creator.create("Individual", array.array, typecode="d", fitness=creator.FitnessMax)
#创建一个float8的数组

与creator.create("Individual", list, fitness=creator.FitnessMax)类似，这里的list是列表，其对象没有约束，可以是数值也可以是字符。而array约束了对象的类型为float8.
所以是其变体。

✋小课堂

array(typecode [, initializer]) -> array
class array(builtins.object)

• 返回一个数组。可初始化。存储的对象类型受到指定的约束。
• 参数 typecode:约束对象的类型

Type code	C Type	Minimum size in bytes
b	signed integer(有符号整数)	1
B	unsigned integer(无符号整数)	1
“u”	Unicode字符	2（请参阅注释）
‘h’	有符号整数	2
“H”	无符号整数	2
‘i’	有符号整数	2
“I”	无符号整数	2
‘l’	有符号整数	4
“L”	无符号整数	4
‘q’	有符号整数	8（见注释）
“Q”	无符号整数	8（见注释）
‘f’	浮点	4
‘d’	浮点	8

⭐️ numpy.ndarray

creator.create("Individual", numpy.ndarray, fitness=creator.FitnessMax)
#创建了数组

2.3 Permutation 排列

排列表示的个体几乎与一般列表个体相似。事实上，它们都继承自基本 list 类型。唯一的区别是，我们需要生成一个随机排列，并将该排列提供给个人，而不是用一系列浮点数填充列表。

基因遗传算法中，比较常用的基因表达方法有：实数(浮点数)，二进制编码，实数编码(排列)……

# 导入库
import random
from deap import base,creator,tools
# creator创建Fiteness和Individual
creator.create("FitnessMin", base.Fitness, weights=(-1.0,))
creator.create("Individual", list, fitness=creator.FitnessMin)
#toolbox注册indices和individual
IND_SIZE=10
toolbox = base.Toolbox()#工具箱
toolbox.register("indices", random.sample, range(IND_SIZE), IND_SIZE)
toolbox.register("individual", tools.initIterate, creator.Individual, #容器
toolbox.indices) #函数

1. 第一个已注册的函数 indices 重定向到该 random.sample() 函数，其参数固定为给定范围内的样本 IND_SIZE 编号。
2. 第二个已注册的函数 individual 是 initIterate() 该函数的快捷方式，其
   container 参数设置为 creator.Individual 类，其 generator 参数 设置为 toolbox.indices() 别名。
3. 调用toolbox.individual()将使用固定参数进行调用 initIterate() ，并返回一个由具有最小化单个目标 fitness 属性的排列组成的完整 creator.Individual 。

✋小课堂

tools.initIterate(container,generator)

• 参数container: 用来存放func导出的数据类型
• 参数generator: 函数，其迭代结果放入container中。
• return :容器的一个实例，其中填充了来自生成器的数据.

实数编码的学习

假设使用[0,1,2,3,4,5,6,7,8,9]=range(10)的一个排列作为基因编码。
方法一：random.shuffle打乱列表的顺序
其特点是在原列表上打算顺序，如果制定多个individual,则每打乱一次，需要生成一个副本用来存档。
方法二：random.sample随机抽样生成。
其特点是不重复抽样，如果在列表中连续抽取10次，则可以生成一个排列。
random.sample(range(10),10)
return:[1, 0, 4, 9, 6, 5, 8, 2, 3, 7] ,这是一个list
✋小课堂

特别的,每次从range10中抽取，但抽取的个数不一致的时候。可以使用partial(来自于functools)(from functools import partial).固定某个函数的部分参数。

gen_idx_1 =partial(random.sample, range(10), 10) 
# 每次从range(10)中随机抽样10次固定为一个函数。
gen_idx_2 =partial(random.sample, range(10), 5) 
# 每次从range(10)中随机抽样5次固定为一个函数。

gen_idx_3 =partial(random.sample, range(10) ) 
gen_idx_3(5) #抽取5次
# 每次从range(10)中随机抽样某次固定为一个函数。

gen_idx_4 =partial(random.sample, k=10 ) 
gen_idx_4(range(20)) #从range(20)中抽取
# 每次从未知的一个列表中抽取10次。

😄Question 1
根据前面实数的编码，sample(range(IND_SIZE),IND_SIZE)可以获得一个排列，为什么还要通过toolbox.register注册为"indices"呢？
因为当前与fitness绑定的为creator.Individual ,需要将 排列 放入该容器中。tools中的操作中第一个带向为容器(container),第二个为函数类型。这里的random.sample是一个迭代类型的函数，所以选择了工具箱中的函数tools.initIterate.
而注意到sample(range(IND_SIZE),IND_SIZE)是一个列表或者说一个一个可迭代的对象而不是一个函数。它是无法放在工具箱中的第二个参数的位置的。属性不正确。

😄Question 2
实数编码中获得排列的方法，还有random.shuffle.那么如何使用它的方式生成individual呢？
未知。因为目前已知的tools中的初始化工具就三个

• tools.initRepeat 重复
• tools.initIterate迭代
• tools.initCycle重复迭代

✋小课堂

initCycle(container, seq_func, n=1)

• 参数container:存放函数的结果类型
• 参数seq_func: 函数们的列表
• 参数n:函数列表迭代的次数

# 定义了两个函数，并放入列表
gen_idx_1 =partial(random.sample, range(10), 10) 
gen_idx_2 =partial(random.sample, range(10), 5) 
seq_func=[gen_idx_1,gen_idx_2]
# 重复两次，每次迭代列表中的函数
tools.initCycle(list,seq_func,2)

结果：

[[1, 0, 4, 9, 6, 5, 8, 2, 3, 7], #循环第一次，迭代第一函数gen_idx_1
 [0, 9, 1, 7, 6], #循环第一次，迭代第二个函数gen_idx_2
 [8, 0, 3, 5, 6, 4, 7, 9, 1, 2],#循环第二次，迭代第一个函数
 [0, 2, 6, 8, 7]]#循环第二次，迭代第二个函数

2.4. Arithmetic Expression 算术表达式

from deap import gp
gp=Genetic Programming 遗传编程

下一个常用的个体是数学表达式的原始树(prefix tree )。
PrimitiveTree 对象通常与特定的适应度函数相关联，该函数用于评估个体的性能。在进化过程中，通过选择、交叉和变异等遗传操作，这些树状结构会不断演变，以寻找解决给定问题的最优或近似最优解。
要创建一个 PrimitiveTree 对象，你通常需要首先定义一个 PrimitiveSet，它包含了可用于构建树的所有原始操作符(primitives)和终端(terminals)。然后，你可以使用DEAP提供的工具来生成和初始化这些树状结构。

import operator # #包含基本操作符，如加减乘
from deap import base, creator, tools, algorithms,gp

#定义操作符的集合(将operator放入集合pset)
pset = gp.PrimitiveSet("MAIN", arity=1)#创建一个名为 "MAIN" 的原语集，并设置其参数个数为 1
pset.addPrimitive(operator.add, 2)
pset.addPrimitive(operator.sub, 2)
pset.addPrimitive(operator.mul, 2)
#creator创建适应度和个体
creator.create("FitnessMin", base.Fitness, weights=(-1.0,))
creator.create("Individual", gp.PrimitiveTree, fitness=creator.FitnessMin,
               pset=pset)
#toolbox注册操作函数和个体
toolbox = base.Toolbox()
toolbox.register("expr", gp.genHalfAndHalf, pset=pset, min_=1, max_=2)
toolbox.register("individual", tools.initIterate, creator.Individual,
 toolbox.expr)

🐒解析

1. PrimitiveSet 包含我们个人可以使用的所有可能的数学运算符。
2. 在这里，集合被称为" MAIN" ，并具有由 arity 定义的单个变量。运算符add(), sub() 和 mul() 被添加到primitive set中，每个运算符的 arity 为 2. （例如，add表示+，需要2个变量）
3. 创建一个“FitnessMin"类别名，基类是base.Fitness,属性是weights=(-1.0)
4. 创建一个”Individual"类别名，基类是gp.PrimitiveTree,属性1为fitness=creator.FitnessMin;属性2为pset=pset.
5. gp.PrimitiveTree是专门为优化遗传编程操作而格式化的树。树用列表表示，其中节点被附加，或者假设在用基元和终端列表初始化此类对象时已经被附加，例如用方法gp.generate以深度优先顺序生成。附加到树的节点需要有一个属性arity，该属性定义了基元的arity。终端节点的arity应为0。
6. 调用 toolbox.individual() 将很容易返回一个完整的个体，该个体是前缀树形式的算术表达式，具有最小化的单个目标适应度属性。

✋小课堂

genHalfAndHalf(pset, min_, max_, type_=None)

• 参数pset：原始操作符(primitives)的集合
• 参数min_: 生成树的最小高度
• 参数max_:生成树的最大高度。
• 参数type_:调用时返回树的类型，如果是默认状态“None",则返回pset.ret的类型。
• retrun:要么一个完整的树，要么一个生长中的树。

2.5 Evolution Strategy

个体的进化策略略有不同，因为它们通常包含两个列表，一个用于实际个体，一个用于其突变参数.这次，我们不适用List基类，二十继承一个包含个体和策略(the individual and the strategy)的array.array类。由于没有helper function(辅助函数)可以在单个对象(single object)中生成(generate)两个不同向量(vectors),我们需要自己定义这样的函数。inintES()函数接收两个类(classes)且可以实例化(instantiates)他们, 且为给定了大小的个体(individuals)提供范围内生成的随机树。

import array
import random

from deap import base, creator, tools
#creator创建适应度，个体，策略
creator.create("FitnessMin", base.Fitness, weights=(-1.0,))
creator.create("Individual", array.array, typecode="d",
               fitness=creator.FitnessMin, strategy=None)
creator.create("Strategy", array.array, typecode="d")#策略是个数组，且‘d'表示float8
#自定义初始化函数
def initES(icls, scls, size, imin, imax, smin, smax):
"""
参数icls:
参数scls:
参数size：
参数imin:
参数imin:
参数imax:
参数smin:
参数smax:
"""
    ind = icls(random.uniform(imin, imax) for _ in range(size))
    ind.strategy = scls(random.uniform(smin, smax) for _ in range(size))
    return ind

IND_SIZE = 10
MIN_VALUE, MAX_VALUE = -5., 5.
MIN_STRAT, MAX_STRAT = -1., 1. 

toolbox = base.Toolbox()
toolbox.register("individual", initES, creator.Individual,
                 creator.Strategy, IND_SIZE, MIN_VALUE, MAX_VALUE, MIN_STRAT, 
                 MAX_STRAT)

调用toolbox.individual()将很容易返回一个完整的进化策略，其中包含策略向量和最小化的单个目标适应度属性。

2.6 Particle 粒子

粒子(Particle)是另一种特殊类型的个体，因为它通常具有速度(speed)并且通常记住其最佳位置(best position)。
这种类型的个人的创建方式（再次）与从列表中继承的方式相同。这次，speed 、 best 和速度限制 （ smin ， smax ） 属性将添加到对象中.同样，还注册了了初始化函数initParticle(), 以生成接收粒子类别、大小、域和速度限制的个体作为参数。

import random
from deap import base, creator, tools
#creator创建了适应度、粒子
creator.create("FitnessMax", base.Fitness, weights=(1.0, 1.0))
creator.create("Particle", list, fitness=creator.FitnessMax, speed=None,
               smin=None, smax=None, best=None)
#定义了粒子的初始化函数
def initParticle(pcls, size, pmin, pmax, smin, smax):
    part = pcls(random.uniform(pmin, pmax) for _ in range(size))
    part.speed = [random.uniform(smin, smax) for _ in range(size)]
    part.smin = smin
    part.smax = smax
    return part
#注册生成粒子
toolbox = base.Toolbox()
toolbox.register("particle", initParticle, creator.Particle, size=2,
                 pmin=-6, pmax=6, smin=-3, smax=3)

调用 toolbox.particle() 将很容易返回一个完整的粒子，该粒子具有速度向量和适应度属性，用于最大化两个目标。

2.7 A Funky One 时髦的

假设您的问题有非常具体的需求，也可以非常容易地构建自定义个人。使用该 initCycle() 函数创建的下一个个体是交替整数和浮点数的列表 。

import random
from deap import base, creator, tools
#creator创建了适应度、个体
creator.create("FitnessMax", base.Fitness, weights=(1.0, 1.0))
creator.create("Individual", list, fitness=creator.FitnessMax)

toolbox = base.Toolbox()

INT_MIN, INT_MAX = 5, 10
FLT_MIN, FLT_MAX = -0.2, 0.8
N_CYCLES = 4

toolbox.register("attr_int", random.randint, INT_MIN, INT_MAX) #注册随机生成整数的函数
toolbox.register("attr_flt", random.uniform, FLT_MIN, FLT_MAX)#注册随机生成浮点数的函数
toolbox.register("individual", tools.initCycle, creator.Individual,
                 (toolbox.attr_int, toolbox.attr_flt), n=N_CYCLES)#注册个体

3、Population 种群

种群很像个体。它们不是用属性初始化的，而是用个体、策略或粒子填充的。

3.1 Bag 袋子

袋子填充是最常用的类型。它没有特定的顺序，尽管它通常使用list实现。由于袋子没有特殊属性，因此不需要任何特殊类别。直接使用工具箱和initRepeat()函数初始化种群.

toolbox.register("population", tools.initRepeat, list, toolbox.individual #注册种群

调用 toolbox.population() 将很容易地返回列表中的完整种群，前提是必须多次重复重复帮助程序作为种群函数的参数。以下示例生成一个具有 100 个个体的种群。

toolbox.population(n=100) #调用函数，生成100个个体

3.1 Grid 网格

网格种群是结构化种群的一种特例，其中相邻的个体彼此有直接影响。个体分布在网格中，每个单元格包含一个个体。但是，它的实施与袋子人口列表仅不同，因为它由个体列表(lists of individuals)组成。

toolbox.register("row", tools.initRepeat, list, toolbox.individual, n=N_COL) #生成行
toolbox.register("population", tools.initRepeat, list, toolbox.row, n=N_ROW)#由行生成网格

调用 toolbox.population() 将很容易返回一个完整的总体，其中可以使用两个索引访问个人，例如 pop[r][c] 。目前，没有专门针对结构化人群的算法，我们正在等待您的提交。

3.3 Swarm 群

群体(swarm)用于粒子群体优化。从某种意义上说，它的不同之处在于它包含一个通信网络。最简单的网络是完全连接的网络，其中每个粒子都知道任何粒子访问过的最佳位置。这通常是通过将全局最佳位置复制到 gbest 属性，将全局最佳适应度复制到 gbestfit 属性来实现的。

creator.create("Swarm", list, gbest=None, gbestfit=creator.FitnessMax) #创建群，继承list类
toolbox.register("swarm", tools.initRepeat, creator.Swarm, toolbox.particle)#注册群，使用'重复初始化'函数

呼叫 toolbox.swarm() 将很容易返回一个完整的群体。每次评估后， gbest 算法应设置 和 gbestfit 以反映最佳找到的位置和适应度。

3.4 Demes 子种群

deme 是包含在种群中的子种群。它类似于岛屿模型中的岛屿。Demes 只是亚种群，实际上与种群没有什么不同，除了它们的名字。在这里，我们创建一个包含 3 个 demes 的种群，每个种群使用 initRepeat() 函数的 n 参数具有不同数量的个体。

#注册demes
toolbox.register("deme", tools.initRepeat, list, toolbox.individual)

DEME_SIZES = 10, 50, 100 #这是个迭代对象？
population = [toolbox.deme(n=i) for i in DEME_SIZES] #建立了3个deme

3.5 Seeding a Population 播种种群

有时，可以使用第一个猜测(guess)种群来初始化进化算法。使用非随机个体初始化种群的关键思想是有一个将内容作为参数的个体初始化器(individual initializer)。

import json
from deap import base,creator
# 创建适应度、个体
creator.create("FitnessMax", base.Fitness, weights=(1.0, 1.0))
creator.create("Individual", list, fitness=creator.FitnessMax)
#定义初始化个体的函数
def initIndividual(icls, content):
    return icls(content)
#定义初始化种群的函数
def initPopulation(pcls, ind_init, filename):
    with open(filename, "r") as pop_file:
        contents = json.load(pop_file)
    return pcls(ind_init(c) for c in contents)
#注册个体猜测，种群猜测
toolbox = base.Toolbox()
toolbox.register("individual_guess", initIndividual, creator.Individual)
toolbox.register("population_guess", initPopulation, list, toolbox.individual_guess, "my_guess.json")

population = toolbox.population_guess()

种群将从包含第一个猜测个体列表的文件中 my_guess.json 初始化。此初始化可以与常规初始化相结合，以具有部分随机和部分非随机个体。请注意，的定义 initIndividual() 和注册 individual_guess() 是可选的，因为列表的默认构造函数是相似的。删除这些行会导致以下结果：

oolbox.register("population_guess", initPopulation, list, creator.Individual, "my_guess.json"

二、案例一元函数取极值

一元函数取极值（完整版）–二进制编码
函数为：
$$h(x)=(x^2+x)cos(2x)+x^2+x$$
自变量$x$的取值范围为：$[-30,30]$
求该函数在范围内的最大值。

1. 定义适应度、个体

# 1. 导入库
import numpy as np
from deap import base, tools, creator, algorithms
import random #随机库
from scipy.stats import bernoulli #导入伯努利分布函数
# 2.定义适应度，单目标，求最大值。
#定义问题
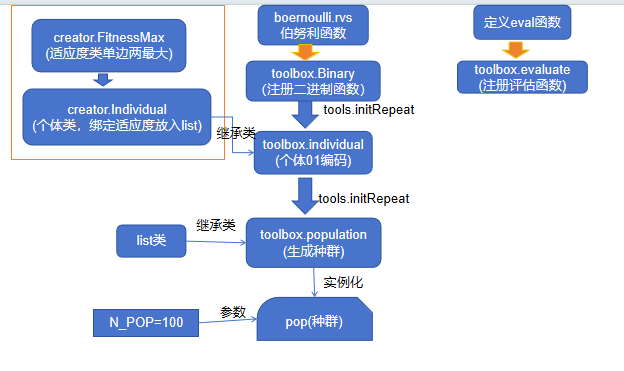
creator.create('FitnessMax',base.Fitness,weights=(1.0,))#单变量，求最大值
# 3. 定义个体
## 3.1 与适应度绑定，继承list类
creator.create('Individual',list,fitness = creator.FitnessMax)#创建individual类
## 3.2 注册二进制函数
GENE_SIZE = 26
toolbox = base.Toolbox()
toolbox.register('Binary',bernoulli.rvs,0.5)#创建01随机的序列，0,1的概率各是0.5
## 3.3 注册个体
toolbox.register('individual',tools.initRepeat,
creator.Individual,
toolbox.Binary,
n=GENE_SIZE)#正式注册个体

此外使用bernouli库来对每个个体的26个基因进行随机的预编码供之后使用。如果需要检查自己编写的个体是否正确，可以使用以下代码打印出来一个个体检查：

print(toolbox.individual())

out:
[0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 1] 26位
✋课堂

1. creator.create("name",class,参数)，前两个必要的，参数是可选的。
2. bernoulli.rvs(0.5),生成0和1的概率为0.5.生成的一位随机数。如果bernoulli.rvs((0.2,0.6))生成的二位的随机数[1 1], [0 1]……，0.2是第一个概率，0.6是第二个概览。
3. tools.initRepeat,调用toolbox.Binary函数GENE_SIZE次，其结果放入creator.Individual.并起别名为”individual".

2. 定义解码函数注册评估函数

这是用01二进制表示的基因，要转成实数，才能计算其适应度。

我们需要求解的值当然是10进制的，但是个体在进行交叉变异等一系列操作的时候是二进制的，显然我们需要一个解码机制，令需要使用10进制的时候将解从二进制转化到10进制。
  解码函数如下所示，num为某个个体的绝对长度，这个长度显然需要换算到坐标轴上来得到具体的值。
  评价函数在该问题中就是需要求解的一元函数，显然在函数中的值越大，就越接近极值这个答案。

## 4.1 解码函数
def decode(individual):#解码函数
    num = int(''.join([str(_) for _ in individual]),2)
    x = -30 + num * 60 /(2**26 - 1)#左边界是-30
    return x#返回真实值（十进制）
## 4.2 计算一元函数
def eval(individual):#评价函数，先解码，后评价适应度
    x = decode(individual)#先解码
    return ((np.square(x) + x) * np.cos(2*x) + np.square(x) + x),#返回适应度
## 4.3注册评价函数
toolbox.register('evaluate',eval)

1. ''.join([str(_) for _ in individual] :join前面的表示一个空字符串，join表示将括号内的元素添加到前面的字符串。括号内是一个列表推导式。individual是一个列表，对每个元素通过str()变为字符，加入到前面字符串中。individual = [1, 0, 1, 1],则变为了字符串“1011”。
2. int("1011",2):是将一个字符串将二进制转化为10进制。
3. 一个8位最大的二进制是“11111111”，转化为实数是$255=2^8-1$,最小实数为0.那么$num/(2^{26}-1)$就是把数字缩小到0~1之间。我们需要的是【-30，30】，即可以通过扩张为到【0，60】，向左水平平移30个单位即可。因此有： x = -30 + num * 60 /(2**26 - 1)

3. 注册种群和计算适应度

N_POP = 100#种群内个体数量
toolbox.register('population',tools.initRepeat,list,toolbox.individual)#注册种群
pop = toolbox.population(n=N_POP)#得到初始种群

fitnesses = map(toolbox.evaluate,pop)#计算初始种群的适应度，先计算得到和种群对应的适应度阵列
for ind,fit in zip(pop,fitnesses):#使用循环将适应度阵列中的元素赋值给种群中个体的适应度变量
    ind.fitness.values = fit#适应度赋值

✋解析

toolbox.population的注册

1. 使用初始化工具函数为tools.initRepeat
2. 根据附录A可知，第一个参数为存储空间，即list;第二个参数为调用的函数为toolbox.individual,这个是生成个体的二进制编码函数(编码长度为26)，还应该有第三个参数n,表示重复调用的次数。但这里省略掉该参数。使得toolbox.pupulation变成functools.partial对象。即预设一部分的参数了。
3. toolbox.population(n=N_POP)即调用第3个参数n了,完成实例化的过程。

fitnesses的搭建

1. pop是一个二维的列表。长度为100=N_POP,每个元素是个列表，长度为26=GENE_SIZE。它也可以是一个迭代序列。
2. toolbox.evaluate是一个注册函数。
3. map(function, iterable, ...)即对每个迭代对象应用function函数。返回一个迭代序列。
4. fitnesses应该是这样的迭代序列：(0.32900347829180987,)，(460.3846995613898,)，(4.257068286089994,)，(27.416912886562894,)，
   (14.868451739098727,)，……
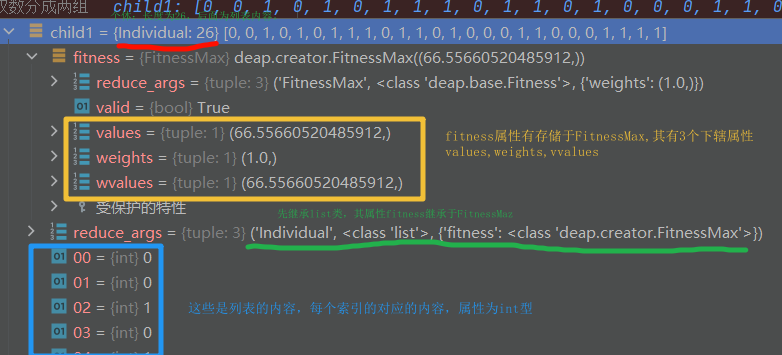
5. ind类似[1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 0],fit类似(27.23061240638161,)
6. ind.fitness.values为什么如此写？ind是for循环的迭代元素。即个体individual. 它存储空间creator.Individual类，且具有属性fitness=creator.FitnessMax. 而FitnesMax其存储空间为base.Fitness.而base.Fitness具有参数属性values,和其他属性weights和vvalues.其中weights在初始设置为(1.0),其他属性为设置。见图
   

关系图

4. 注册操作算子

在遗传算法的迭代计算中，需要执行的最基本的三种操作为选择、交叉、变异。因此需要为这三种操作注册对应的方法，这里使用的是锦标赛选择法，均匀交叉法，位翻转突变法。

使用内置函数
  此外，在deap中，如果使用deap的内置遗传算法，那么注册的名称必须采用固定的形式：toolbox.evaluate、toolbox.select、toolbox.mate、toolbox.mutate。
  
注册自定义函数
  这里不使用内置遗传算法，因此注册名称可以自定义。
  这里也可以看到deap库的工具注册机制是如何实现的：以注册锦标赛工具为例，注册好的方法名为tourSel，它的本体是方法tools.selTournament()，只是换了一个名字添加到了库的工具箱里面。其后的所有内容其实都是方法tools.selTournament()的传参。

锦标赛选择法核心思想是，在每次进化的过程中从父代中随机选取一定数量的个体，并在这些个体中选取适应度最高的个体进行遗传操作，对这一过程进行重复操作，直至子代种群与父代种群的规模相同。通过这一过程，极大的保持了种群的多样性。

N_GEN = 100#迭代数量
CXPB = 0.5#交叉概率
MUTPB = 0.2#变异概率

toolbox.register('tourSel',tools.selTournament,tournsize = 2)#注册锦标赛工具
toolbox.register('crossover',tools.cxUniform)#注册交叉工具
toolbox.register('mutate',tools.mutFlipBit)#注册变异工具

✋ 解析

1. 注册tourSel:在注册函数的时候借用了tools.selTournament函数，其变量参数有3个，只预先设置了tournsize=2,即每轮参加比赛的个体数。具体见附录D.
2. 注册crossover:交叉函数
3. 注册mutate.突变函数

5. 循环迭代过程

使用代数来控制循环，因为在不清楚该问题的适应度情况下，贸然使用适应度作为阈值控制循环并不合适。
  在迭代循环中依次实现：选择，交叉，变异。这里需要注意，在交叉，变异之后，该个体的适应度通常会产生变化（自身构造变了），因此需要将原先的适应度删掉，再将这些个体重新赋予适应度。

for gen in range(N_GEN):#利用代数控制循环
    selectedTour = toolbox.tourSel(pop,N_POP)#对种群进行选择
    selectedInd = list(map(toolbox.clone,selectedTour))#复制个体
    ####交叉####
    for child1,child2 in zip(selectedInd[0::2],selectedInd[1::2]):#将选择好的个体按照单数双数分成两组
        if random.random() < CXPB:#满足交叉概率
            toolbox.crossover(child1,child2,0.5)#将这两组进行交叉
            del child1.fitness.values#交叉完适应度肯定也变了，所以先删掉发生交叉的个体的适应度
            del child2.fitness.values#同上，毕竟有两组
    ###突变###
    for mutant in selectedInd:#对选择好的种群遍历
        if random.random() < MUTPB:#满足变异概率
            toolbox.mutate(mutant,0.3)#变异
            del mutant.fitness.values#变异了适应度也变了，先把适应度删掉
    ###删掉适应度的个体重新计算适应度###
    invalid_ind = [ind for ind in selectedInd if not ind.fitness.valid]#选择出删掉适应度的个体
    fitnesses = map(toolbox.evaluate,invalid_ind)#得到与种群对应的适应度阵列
    for ind,fit in zip(invalid_ind,fitnesses):#将适应度阵列中的元素赋值给种群个体的适应度变量 
        ind.fitness.values = fit#适应度赋值
    ####更新与记录###
    pop[:] = selectedInd#重新赋值给原先种群变量，进入下一轮操作
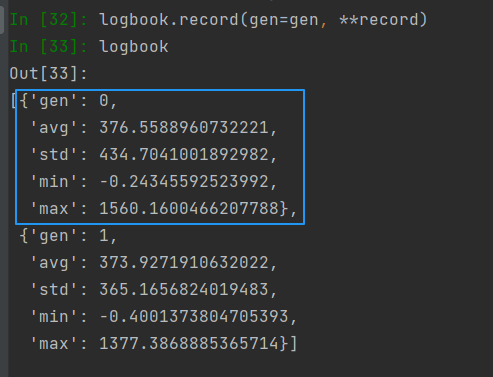
    record = stats.compile(pop)
    logbook.record(gen=gen, **record)

✋

1. selectedTour长度为100.在原pop中每轮比赛二选一，共选择出100个个体。selectedTour类似于pop，但是二者不相等。 其长度为100=N_POP，每个元素为individual.
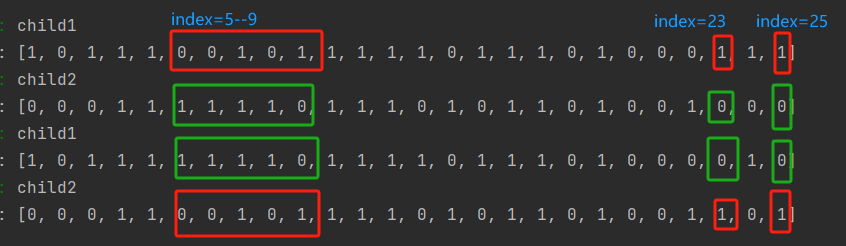
2. selectedInd是selected的复制种群。toolbox.clone深度复制操作。
3. selectedInd[0::2]表示步长为2从序列为0开始的子序列，即双数组；selectedInd[1::2]步长为2从序列1开始的子序列，即单数组。child1的序列为0,2,4,6，……，98；child2的序列为1,3,5，……99。
4. toolbox.crossover(child1,child2,0.5) 举例说明。如下在index=5-9,index=23,index=25的位置进行了交换。获得了新的child1和child2.
   
5. stats.compile(data) 计算统计信息的对象序列。返回的类型如下
   {‘avg’: 376.5588960732221,
   ‘std’: 434.7041001892982,
   ‘min’: -0.24345592523992,
   ‘max’: 1560.1600466207788}
6. logbook = tools.Logbook().记录后的寄过类似于如下：
   

6. 选择最佳结果

这样的记录缺点就是在往届中可能存在最优的个体但是不能够保存。

##循环结束后
logbook.header = 'gen', 'nevals', 'avg', 'std', 'min', 'max'
print(logbook)
# 显示适应度最大的变量
index = np.argmax([ind.fitness for ind in pop])
x = decode(pop[index])
print('best solution:' + str(x) + ' function value:' + str(pop[index].fitness))

附录一：重要函数解析

A.tools.initRepeat

initRepeat(container, func, n)
Call the function func n times and return the results in a container type container. 调用函数’fuc’ 有‘n’次，并将返回的结果放入容器container中。

• 参数container：func导出的数据类型
• 参数 func: 将被调用n次以填充容器的函数
• 参数n:重复调用的次数

B. tools.initIterate

tools.initIterate(container,generator)

• 参数container: 用来存放func导出的数据类型
• 参数generator: 函数，其迭代结果放入container中。
• return :容器的一个实例，其中填充了来自生成器的数据.

C.tools.initCycle

initCycle(container, seq_func, n=1)

• 参数container:存放函数的结果类型
• 参数seq_func: 函数们的列表
• 参数n:函数列表迭代的次数

D. tools.selTournament

selTournament(individuals, k, tournsize, fit_attr='fitness')

• 参数individuals:个体列表
• 参数k:被选择的个体个数
• 参数tournsize: 参加每场比赛的个体数目
• 参数fit_attr: 用作选择标准的个人属性

E.tools.cxUniform

cxUniform(ind1, ind2, indpb)

• 参数ind1:第一个参加交叉赛的个体
• 参数ind2:第二个参加交叉赛的个体
• 参数indpb:每个属性交换的独立概率。
• return:返回两个个体的元组。

F.tools.mutFlipBit

mutFlipBit(individual, indpb)

• 参数individual:突变的个体
• 参数indpb:每个属性翻转的独立概率

G.tools.Logbook

class Logbook(builtins.list)

1. record(self, **infos):参数**infos是字典类型的数据。记录信息
2. select(self, *names)对记录的数据进行选择

log = Logbook()
log.record(gen=0, mean=5.4, max=10.0)
log.record(gen=1, mean=9.4, max=15.0)
log.select("mean")#out:[5.4, 9.4]
log.select("gen", "max")#out:([0, 1], [10.0, 15.0])
###新案例
log.record(**{'gen': 0, 'fit': {'mean': 0.8, 'max': 1.5}, ... 'size': {'mean': 25.4, 'max': 67}})
log.record(**{'gen': 1, 'fit': {'mean': 0.95, 'max': 1.7}, ... 'size': {'mean': 28.1, 'max': 71}})
log.chapters['size'].select("mean")#out: [25.4, 28.1]
log.chapters['fit'].select("gen", "max")#out:([0, 1], [1.5, 1.7])

附录二：结果记录

gen nevals avg std min max
0 375.9 394.707 0.0378987 1529.28
1 441.763 433.525 0.0924669 1540.14
2 546.777 505.102 0.302198 1652.97
3 666.443 558.051 0.587084 1655.18
4 815.168 584.989 -0.349772 1655.18
5 707.65 558.332 0.0660801 1655.18
6 710.868 592.954 -0.377957 1656
7 729.566 608.277 0.00486766 1656
8 643.852 608.521 -0.364684 1656
9 702.494 623.59 0.000586054 1656
10 766.011 609.097 0.873934 1655.2
11 750.477 587.761 0.0301504 1544.32
12 779.213 610.523 -0.298943 1544.26
13 864.478 624.26 0.562563 1544.32
14 952.687 630.442 -0.298101 1543.72
15 1102.39 546.517 0.287866 1544.26
16 1201.18 494.508 0.0139055 1544.3
17 1205.26 516.755 -0.0277024 1544.26
18 1233.62 508.19 2.45636 1544.28
19 1253.72 511.578 0.580995 1544.28
20 1190.06 571.011 0.146735 1544.28
21 1228.08 543.912 0.425438 1544.28
22 1251.08 556.679 0.108038 1544.28
23 1321.82 503.59 0.00415933 1544.28
24 1350.77 471.924 0.500722 1544.28
25 1369.68 432.636 4.755 1544.28
26 1302.95 536.641 0.0972314 1544.28
27 1309.55 509.413 8.09302 1544.28
28 1207.31 581.453 0.0930679 1544.28
29 1266.2 524.239 0.0950694 1544.28
30 1210.3 577.677 0.139966 1544.28
31 1232.71 550.386 0.0707371 1544.28
32 1189.55 580.007 0.10881 1544.28
33 1180.05 587.282 0.391655 1544.29
34 1228.52 537.767 1.20234 1544.29
35 1173.75 597.334 0.0474645 1544.29
36 1266.72 543.569 0.000282944 1544.29
37 1238.4 544.391 0.60313 1544.29
38 1328.92 470.676 0.149761 1544.29
39 1158.54 618.148 -0.176273 1544.29
40 1159.91 599.135 0.0459915 1544.29
41 1202.26 565.517 0.550964 1544.29
42 1327.51 480.73 0.110645 1544.29
43 1227.95 560.139 0.0618206 1544.29
44 1197.3 579.214 0.0282256 1544.32
45 1262.3 526.558 1.05907 1544.32
46 1221.03 574.314 -0.355678 1544.32
47 1260.48 536.579 0.00911884 1544.32
48 1256.48 525.983 0.0596398 1573.84
49 1219.06 560.202 0.00405634 1544.32
50 1289.43 510.384 -0.274271 1544.32
51 1326.31 474.434 0.115063 1544.32
52 1270.69 539.79 0.118017 1544.32
53 1283.84 535.439 0.0960047 1544.32
54 1248.44 577.316 0.137646 1544.32
55 1290.63 493.59 0.110041 1544.32
56 1325.54 468.94 0.0738366 1544.32
57 1328.59 485.187 0.676014 1544.32
58 1261.38 544.075 0.617373 1544.32
59 1283.52 517.444 0.14457 1544.32
60 1253.4 552.49 -0.326191 1544.32
61 1264.92 536.488 1.39276 1544.32
62 1217.61 569.685 0.0772461 1544.33
63 1240.63 546.672 0.464639 1544.33
64 1254.34 535.05 0.0199027 1544.33
65 1272.26 551.861 0.0169924 1544.32
66 1334.06 487.373 0.115062 1544.32
67 1364.84 435.604 0.602819 1544.32
68 1185.21 584.46 0.0679727 1544.32
69 1236.93 540.687 0.129899 1544.32
70 1242.08 549.399 0.485847 1544.32
71 1303.02 472.054 0.593114 1544.33
72 1278.45 525.239 0.154275 1544.33
73 1287.36 495.731 5.17434e-06 1544.33
74 1302.04 512.963 0.143023 1544.33
75 1290.55 534.788 0.0179914 1544.33
76 1250.52 544.868 0.278621 1544.33
77 1296.61 509.192 1.20074 1544.33
78 1240.65 546.011 0.210687 1544.33
79 1238.43 551.794 0.330741 1544.33
80 1220.37 566.626 1.31949 1544.33
81 1243.42 566.249 1.3889 1544.33
82 1266.39 527.641 4.1398 1544.33
83 1381.04 414.569 0.0960579 1544.33
84 1247.29 560.259 0.110323 1544.33
85 1289.35 512.995 -0.0205085 1544.33
86 1313.31 510.691 0.00483559 1544.33
87 1252.3 556.466 0.0355053 1544.33
88 1254.39 539.049 0.20947 1544.33
89 1182.01 596.69 0.00145786 1544.33
90 1335.81 473.12 0.129137 1544.33
91 1226.85 550.731 0.126762 1544.33
92 1202.39 539.228 1.20796 1544.33
93 1339.27 458.826 -0.305481 1544.33
94 1315.64 508.197 0.685893 1544.33
95 1327.55 482.366 9.14075 1544.33
96 1327.82 491.399 0.963968 1544.33
97 1320.45 480.912 0.0417088 1544.33
98 1274.87 544.057 1.24073 1544.33
99 1211.31 590.028 0.96395 1544.33