高效求出两个整数的最大公约数,要尽量优化算法的性能。
def getDiv(a,b):
ma=max(a,b)
mi=min(a,b)
#判断能被整除
if ma%mi==0:
return mi
#递归
return getDiv(ma%mi,mi)
if __name__ == '__main__':
# print(getDiv(10, 25))
print(getDiv(1000, 50))
没错,这确实是辗转相除法的思路。不过有一个问题,当两个整数较大时,做 a%b取模运算的性能会比较差。
更相减损术,出自中国古代的《九章算术》,也是一种求最大公约数的算法。
它的原理更加简单:两个正整数a和b (a>b),它们的最大公约数等于a-b的差值c和较小数b的最大公约数。例如,10和25,25减10的差是15,那么10和25的最大公约数,等同于10和15的最大公约数。
def getDiv(a,b):
#如果相等,就是最大公约数
if a==b:
return a
#求出最大值,最小值
ma=max(a,b)
mi=min(a,b)
#递归调用
return getDiv(ma-mi,mi)
if __name__ == '__main__':
print(getDiv(100, 75))
更相减损术依靠两数求差的方式来递归,运算次数肯定远大于辗转相除法取模方式。如计算10000和1的最大公约数,就要递归9999次!
有什么办法可以既避免大整数取模,又能尽可能地减少运算次数呢?
最优方法:把辗转相除法和更相减损术的优势结合起来,在更相减损术的基础上使用移位运算。
当a和b均为偶数时,gcd (a,b) =2xgcd (a/2,b/2)=2xgcd (a>>1,b>>1)。
当a为偶数,b为奇数时,gcd (a,b) = gcd (a/2,b) = gcd (a>>1,b)。
当a为奇数,b为偶数时,gcd (a,b) = ged (a,b/2) = ged (a,b>>1)。
当a和b均为奇数时,先利用更相减损术运算一次,gcd (a,b) = gcd (b,a-b),此时a-b必然是偶数,然后又可以继续进行移位运算。
其中:gcd是求最大公约数的方法,a是第一个数,b是第二个数。

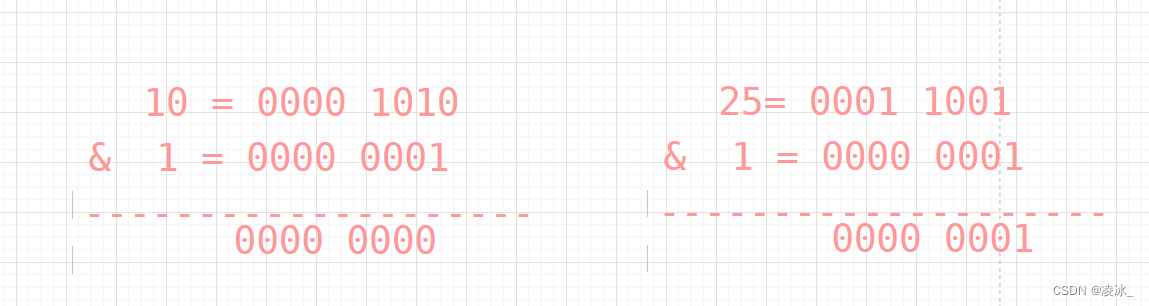
def getDiv3(a,b):
#如果相等,就是最大公约数
if a==b:
return a
#a,b都为偶数,,则a,b都右移1位,再乘以2
if(a&1)==0 and (b&1)==0:
return getDiv3(a>>1,b>>1) <<1
# a为偶数,b为奇数,则a右移1位
elif (a&1)==0 and (b&1)!=0:
return getDiv3(a>>1,b)
# a为奇数,b为偶数,则b右移1位
elif (a&1)!=0 and (b&1)==0:
return getDiv3(a,b>>1)
else:
#求出最大值,最小值
ma=max(a,b)
mi=min(a,b)
#递归调用
return getDiv3(ma-mi,mi)
if __name__ == '__main__':
print(getDiv3(10, 25))
print(getDiv3(10000, 55))总之:
1.辗转相除法:时间复杂度不太好计算,可以近似为O(log (max (a,b)) ),但是取模运算性能较差。
2.更相减损术:避免了取模运算,但是算法性能不稳定,最坏时间复杂度为O (max (a,b) ) 。
3.更相减损术与移位相结合:不但避免了取模运算,而且算法性能稳定,时间复杂度为O(log (max (a,b) ) ) 。