目录

#小A的糖果
删数问题
陶陶摘苹果（升级版）
P5019 NOIP2018 提高组 铺设道路

---

小A的糖果

原文链接:
P3817 小A的糖果 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

题目描述

小 A 有 n 个糖果盒，第 i 个盒中有 a_i 颗糖果。

小 A 每次可以从其中一盒糖果中吃掉一颗，他想知道，要让任意两个相邻的盒子中糖的个数之和都不大于 x，至少得吃掉几颗糖。

输入格式

输入的第一行是两个用空格隔开的整数，代表糖果盒的个数 n 和给定的参数 x。

第二行有 n 个用空格隔开的整数，第 i 个整数代表第 i 盒糖的糖果个数 a_i。

输出格式

输出一行一个整数，代表最少要吃掉的糖果的数量。

样例 #1

样例输入 #1

3 3
2 2 2

样例输出 #1

1

样例 #2

样例输入 #2

6 1
1 6 1 2 0 4

样例输出 #2

11

样例 #3

样例输入 #3

5 9
3 1 4 1 5

样例输出 #3

0

提示

样例输入输出 1 解释

吃掉第 2 盒中的一个糖果即可。

样例输入输出 2 解释

第 2 盒糖吃掉 6 颗，第 4 盒吃掉 2 颗，第 6 盒吃掉 3 颗。

数据规模与约定

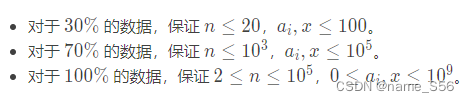
做题思想过程(菜)

#include <bits/stdc++.h>
using namespace std;
int main()
{
	ios::sync_with_stdio(0),cout.tie(0);cin.tie(0);
	int N,x,ans=0,chg;
	cin>>N>>x;
	int num[N];
	for (int i = 0; i < N; i++)
		cin>>num[i];
	for (int i = 1; i < N; i++)
	{
		if (num[i]+num[i-1]>x)
		{
			chg = num[i]+num[i-1]-x;
			num[i] -= chg;
			ans+= chg;
		}
	}
	cout<<ans;	
	return 0;
}

上述问题4个测试点没过

• 原因一: 没开long long
  开了long long 再过俩
• 原因二 : 没 考虑第一个首位
  e.g. 输入

3 10
9999 0 11

正确输出 9990 但是输出了9989 (给减成负数

---

删数问题

题目描述

键盘输入一个高精度的正整数 $N$（不超过 $250$ 位），去掉其中任意 $k$ 个数字后剩下的数字按原左右次序将组成一个新的非负整数。编程对给定的 $N$ 和 $k$，寻找一种方案使得剩下的数字组成的新数最小。

输入格式

输入两行正整数。

第一行输入一个高精度的正整数 $n$。

第二行输入一个正整数 $k$，表示需要删除的数字个数。

输出格式

输出一个整数，最后剩下的最小数。

样例 #1

样例输入 #1

175438 
4

样例输出 #1

13

---

#include <bits/stdc++.h>
using namespace std;
int main()
{
	ios::sync_with_stdio(0),cout.tie(0);cin.tie(0);
	string S;
	cin>>S;
	int k,i;
	cin>>k;
	while(k){
		if(S[0]=='0'){
			S.erase(0,1);
			continue;
		}	// 坑 删的时候怎么有0
		for (i=0;S[i]<S[i+1];)
		{i++;}
		S.erase(i,1);
		k--;
	} 
	while(S[0]=='0'&&S.length()>1)
		S.erase(0,1);
	cout<<S;
	return 0;
}
}

不会(一个点没过,搁置

陶陶摘苹果（升级版）

题目描述

又是一年秋季时，陶陶家的苹果树结了 $n$ 个果子。陶陶又跑去摘苹果，这次他有一个 $a$ 公分的椅子。当他手够不着时，他会站到椅子上再试试。

这次与 NOIp2005 普及组第一题不同的是：陶陶之前搬凳子，力气只剩下 $s$ 了。当然，每次摘苹果时都要用一定的力气。陶陶想知道在 $s<0$ 之前最多能摘到多少个苹果。

现在已知 $n$ 个苹果到达地上的高度 $x_i$，椅子的高度 $a$，陶陶手伸直的最大长度 $b$，陶陶所剩的力气 $s$，陶陶摘一个苹果需要的力气 $y_i$，求陶陶最多能摘到多少个苹果。

输入格式

第 $1$ 行：两个数 苹果数 $n$，力气 $s$。

第 $2$ 行：两个数 椅子的高度 $a$，陶陶手伸直的最大长度 $b$。

第 $3$ 行~第 $3+n-1$ 行：每行两个数 苹果高度 $x_i$，摘这个苹果需要的力气 $y_i$。

输出格式

只有一个整数，表示陶陶最多能摘到的苹果数。

样例 #1

样例输入 #1

8 15
20 130
120 3
150 2
110 7
180 1
50 8
200 0
140 3
120 2

样例输出 #1

4

提示

对于 $100\%$ 的数据，$n\le 5000$, $a\le 50$, $b\le 200$, $s\le 1000$, $x_i\le 280$, $y_i\le 100$。

---

#include <bits/stdc++.h>
using namespace std;

struct Struct {
    int x, y;
};

bool cmp(const Struct& a, const Struct& b) {
    return a.y < b.y;
}

int main() {
    
    ios::sync_with_stdio(0), cout.tie(0), cin.tie(0);
    int n, s;
    cin >> n >> s;
    Struct ap[n];
    int a, b, x, y, f = 0;
    cin >> a >> b;
    for (int i = 0; i < n; i++) {
        cin >> x >> y;
        if (a + b >= x) {
            ap[f].x = x;
            ap[f].y = y;
            f++;
        }
    }
    sort(ap, ap + f, cmp);
    int i=0,ans=0;
	while(s){
		if(s>ap[i].y&&i<f){
			s-=ap[i].y;
			ans++;
			i++;
		}else
			break;
	}
	cout<<ans;
    return 0;
}

为什么不用桶排序…(上面的也没过

![#include <bits/stdc++.h>
using namespace std;

struct Struct {
    int x, y;
};
int to[300];
int main() {
    
    ios::sync_with_stdio(0), cout.tie(0), cin.tie(0);
    int n, s;
    cin >> n >> s;
    int a, b, x, y;
    cin >> a >> b;
    for (int i = 0; i < n; i++) {
        cin >> x >> y;
        if (a + b >= x) {
            to[y]++;
        }
    }
    int ans=0;
		for(int i=0;i<300;i++){
			while(to[i]>0&&s>i){
				s-=i;
				ans++;
				to[i]--;
			}
		}
	cout<<ans;
    return 0;
}

换桶排序了,还是第一个点没过
您猜怎么着,S=0,还有免费的苹果.
while(to[i]>0&&s>=i) 加上=即可

---

铺设道路

[P5019 NOIP2018 提高组] 铺设道路 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

题目描述

春春是一名道路工程师，负责铺设一条长度为 $n$ 的道路。

铺设道路的主要工作是填平下陷的地表。整段道路可以看作是 $n$ 块首尾相连的区域，一开始，第 $i$ 块区域下陷的深度为 $d_i$ 。

春春每天可以选择一段连续区间 $[L,R]$ ，填充这段区间中的每块区域，让其下陷深度减少 $1$。在选择区间时，需要保证，区间内的每块区域在填充前下陷深度均不为 $0$ 。

春春希望你能帮他设计一种方案，可以在最短的时间内将整段道路的下陷深度都变为 $0$ 。

输入格式

输入文件包含两行，第一行包含一个整数 $n$，表示道路的长度。 第二行包含 $n$ 个整数，相邻两数间用一个空格隔开，第 $i$ 个整数为 $d_i$ 。

输出格式

输出文件仅包含一个整数，即最少需要多少天才能完成任务。

样例 #1

样例输入 #1

6   
4 3 2 5 3 5

样例输出 #1

9

提示

【样例解释】
一种可行的最佳方案是，依次选择：
$[1,6]$、$[1,6]$、$[1,2]$、$[1,1]$、$[4,6]$、$[4,4]$、$[4,4]$、$[6,6]$、$[6,6]$。

【数据规模与约定】

对于 $30\%$ 的数据，$1\le n\le 10$ ；
对于 $70\%$ 的数据，$1\le n\le 1000$ ；
对于 $100\%$ 的数据，$1\le n\le 100000,0\le d_i\le 10000$ 。

---

题解太强了(
题解一:贪心

#include<bits/stdc++.h>
using namespace std;
int n,a[100005];
long long ans=0;
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)     cin>>a[i];
	/**/
	for(int i=2;i<=n;i++)     if(a[i]>a[i-1]) ans+=a[i]-a[i-1];
	cout<<ans+a[1];   //+a[1]
	return 0;
}
//其实这个可以不用数组

题解二递推

#include<bits/stdc++.h>
using namespace std;
int n,a[110000],f[110000];
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
		cin>>a[i];
	f[1]=a[1];	//初始化
	for(int i=2;i<=n;i++)
	{
		if(a[i]<=a[i-1])
			f[i]=f[i-1];	//推
		else f[i]=f[i-1]+(a[i]-a[i-1]);  //后面比前面 *深* 时
	}
	cout<<f[n]<<endl;
	return 0;
}