KDTree（K-Dimensional Tree）原理

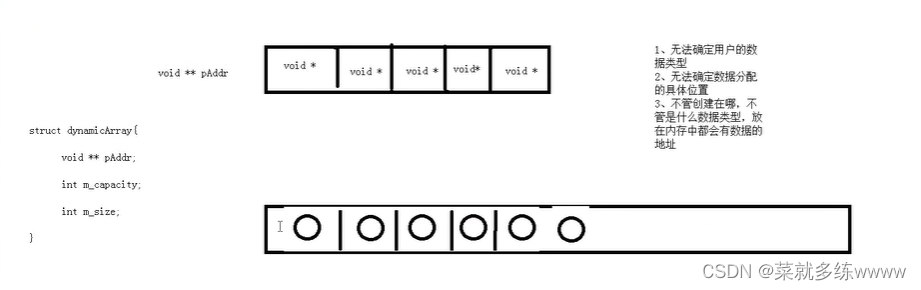
将需要匹配的 K 维空间点建立 K 维树空间索引，在近邻匹配时，输入的点在树中快速检索，即可找到最近邻的点。
在建立空间索引二维树时，算法复杂度介于 $O(lo{g}_{2}n)$和$O(n)$之间。

• 最好的情况下，每次插入点能均匀分割剩余点，算法复杂度为 $O(lo{g}_{2}n)$
• 最坏的情况下，每次插入点其余点都在一个字空间中，树的深度为n，算法复杂度为 $O(n)$
  

步骤

1. 空间索引建立
   • 给定或选择中心节点
   • 依次从各维度分割
   • 按照层次插入点，建立空间索引
2. 最近邻搜索
   • 给定数据点，查询与其距离最近的点
   • 从根节点开始依次向下搜索，进行深度优先遍历，直到与待查询点处于同一子空间的叶子结点
   • 回溯搜索路径、判断路径上其它子节点空间中，是否可能有距离更近的点
     • 如过有可能，跳转到其他子空间去搜索，将其他子节点加入搜索路径
     • 以待查询点为圆心，以待查询点到叶子结点的距离为半径作圆，如果不相交则不必去其他字空间搜索
   • 重复过程，直到搜索路径为空
     

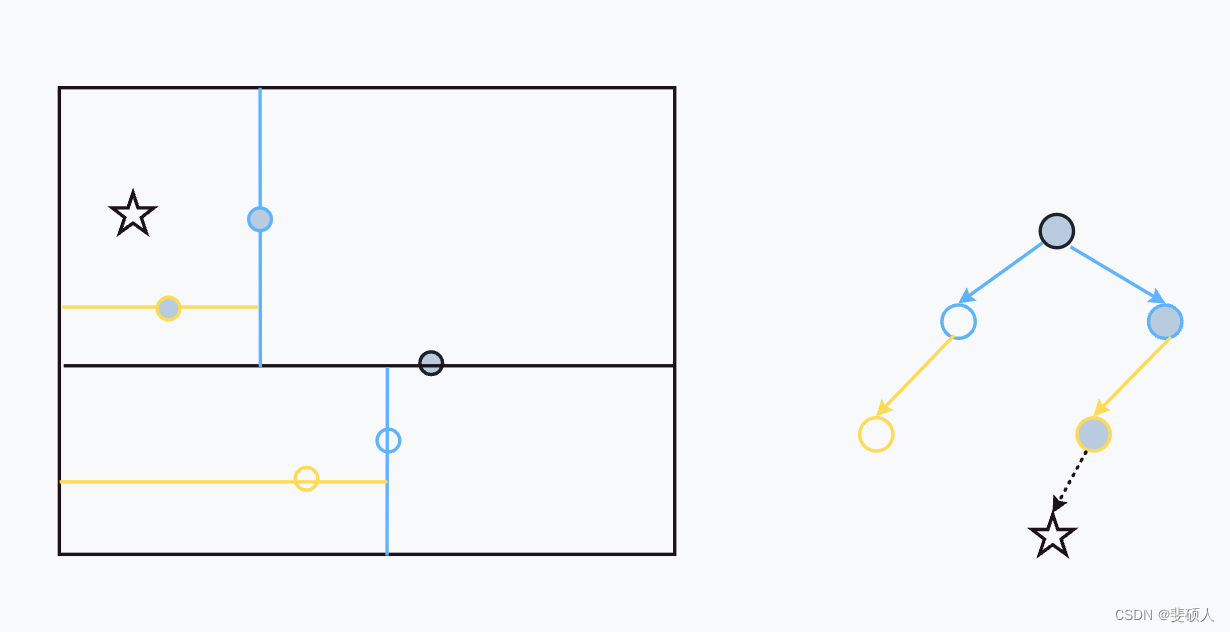
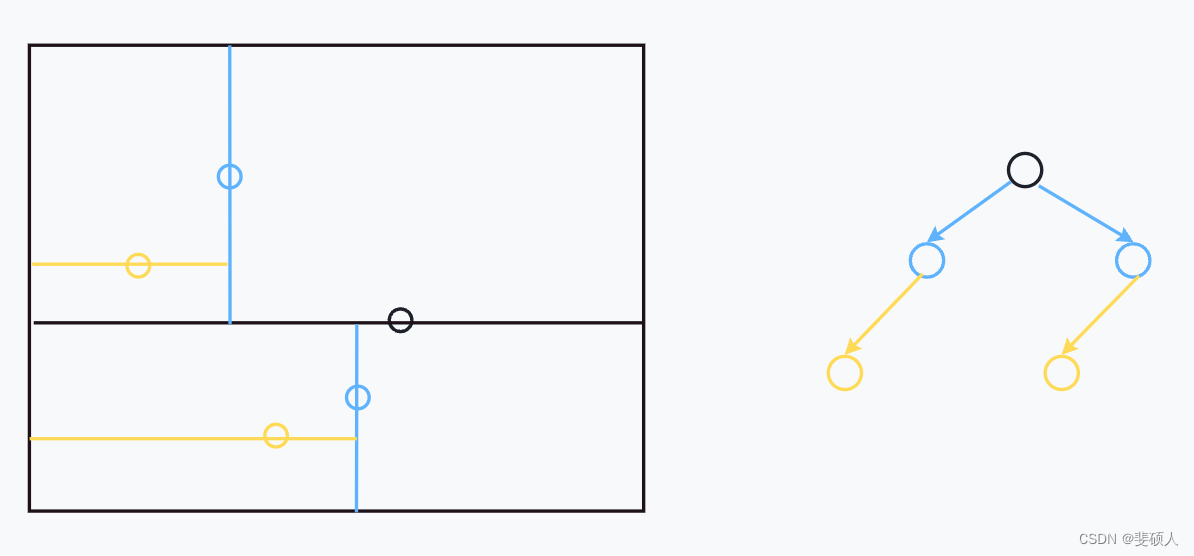
空间索引建立例子¹

• 二维样例：{（2,3），（5,4），（9,6），（4,7），（8,1），（7,2）}
• 根据x轴中位数，选择中心点为(7,2)
• 首先在 x 轴维度上，比较其余点和中心点的大小，划分双支
  • 左支：{(2,3)，(5,4)，(4,7)}
  • 右支：{(9,6)，(8,1)}
• 更新分割轴y轴
• 确定子节点
  • 左节点
    • 在左支中找到y轴的中位数(5,4)
    • 左支数据更新为{(2,3)}，右支数据更新为{(4,7)}
  • 右节点
    • 在右支中找到y轴的中位数(9,6)
    • 左支数据更新为{(8,1)}，右支数据为null。
• 更新分割轴x轴
  • 确定(5,4)的子节点
    • 左节点：由于只有一个数据，所以，左节点为(2,3)
    • 右节点：由于只有一个数据，所以，右节点为(4,7)
  • 确定(9,6)的子节点

相关包

sklearn、SciPy、TransBigData、BioPython 中都提供了 KDTree 相关算法接口

• class sklearn.neighbors.KDTree(X, leaf_size=40, metric=‘minkowski’, **kwargs)
  

• class scipy.spatial.KDTree(data, leafsize=10, compact_nodes=True, copy_data=False, balanced_tree=True, boxsize=None)
  

• transbigdata.ckdnearest(dfA_origin, dfB_origin, Aname=[‘lon’, ‘lat’], Bname=[‘lon’, ‘lat’])

• classBio.KDTree.KDTree.KDTree(dim, bucket_size=1)

案例²

数据

共享单车数据

BIKE_ID	DATA_TIME	LOCK_STATUS	LONGITUDE	LATITUDE
单车ID	数据采集时间	单车开关锁状态	GPS经度	GPS维度

metro_station.csv

KDTree 识别轨道衔接出行

#定义函数，用cKDTree匹配点与点，点与线
import numpy as np
from scipy.spatial import cKDTree
import itertools
from operator import itemgetter
#定义KDTree的函数
def ckdnearest(dfA_origin,dfB_origin,Aname = ['slon','slat'],Bname = ['lon','lat']):
    gdA = dfA_origin.copy()
    gdB = dfB_origin.copy()
    from scipy.spatial import cKDTree
    #为gdB表的点建立KDTree
    btree = cKDTree(gdB[Bname].values)
    #在gdB的KDTree中查询gdA的点,dist为距离,idx为gdB中离gdA最近的坐标点
    dist,idx = btree.query(gdA[Aname].values,k = 1)
    #构建匹配的结果
    gdA['dist'] = dist
    gdA['index'] = idx
    gdB['index'] = range(len(gdB))
    gdf = pd.merge(gdA,gdB,on = 'index')
    #计算
    import CoordinatesConverter
    gdf['dist'] = CoordinatesConverter.getdistance(gdf[Aname[0]],gdf[Aname[1]],gdf[Bname[0]],gdf[Bname[1]])
    return gdf

#读取轨道站点数据
metro_station = pd.read_csv(r'data/metro_station.csv')
metro_station = metro_station.drop_duplicates(subset= 'stationnames')
metro_station = metro_station[['stationnames','lon','lat']]

#匹配起点最近的地铁站
metro_station.columns = ['o_station','o_lon','o_lat']
data_move_metro = ckdnearest(data_move_cleaned,metro_station,Aname = ['slon','slat'],Bname = ['o_lon','o_lat'])
data_move_metro = data_move_metro.rename(columns = {'dist':'o_dist'})

#匹配终点最近的地铁站
metro_station.columns = ['d_station','d_lon','d_lat']
data_move_metro = ckdnearest(data_move_metro,metro_station,Aname = ['elon','elat'],Bname = ['d_lon','d_lat'])
data_move_metro = data_move_metro.rename(columns = {'dist':'d_dist'})
data_move_metro.iloc[:2].T    

#筛选距离地铁站100米范围内的出行数据
data_move_metro = data_move_metro[(data_move_metro['o_dist']<100)|
                (data_move_metro['d_dist']<100)]
data_move_metro.iloc[:2].T

轨道衔接单车骑行范围分析

#选取某站点
station = '同济大学'
#提取地铁站衔接出行的另一端点分布
tmp1 = data_move_metro[(data_move_metro['o_station']==station)&(data_move_metro['o_dist']<=100)][['elon','elat']]
tmp2 = data_move_metro[(data_move_metro['d_station']==station)&(data_move_metro['d_dist']<=100)][['slon','slat']]
tmp1.columns = ['lon','lat']
tmp2.columns = ['lon','lat']
points = pd.concat([tmp1,tmp2])

#转换为GeoDataFrame
points = geopandas.GeoDataFrame(points)
points['geometry'] = geopandas.points_from_xy(points['lon'],points['lat'])

points.plot()

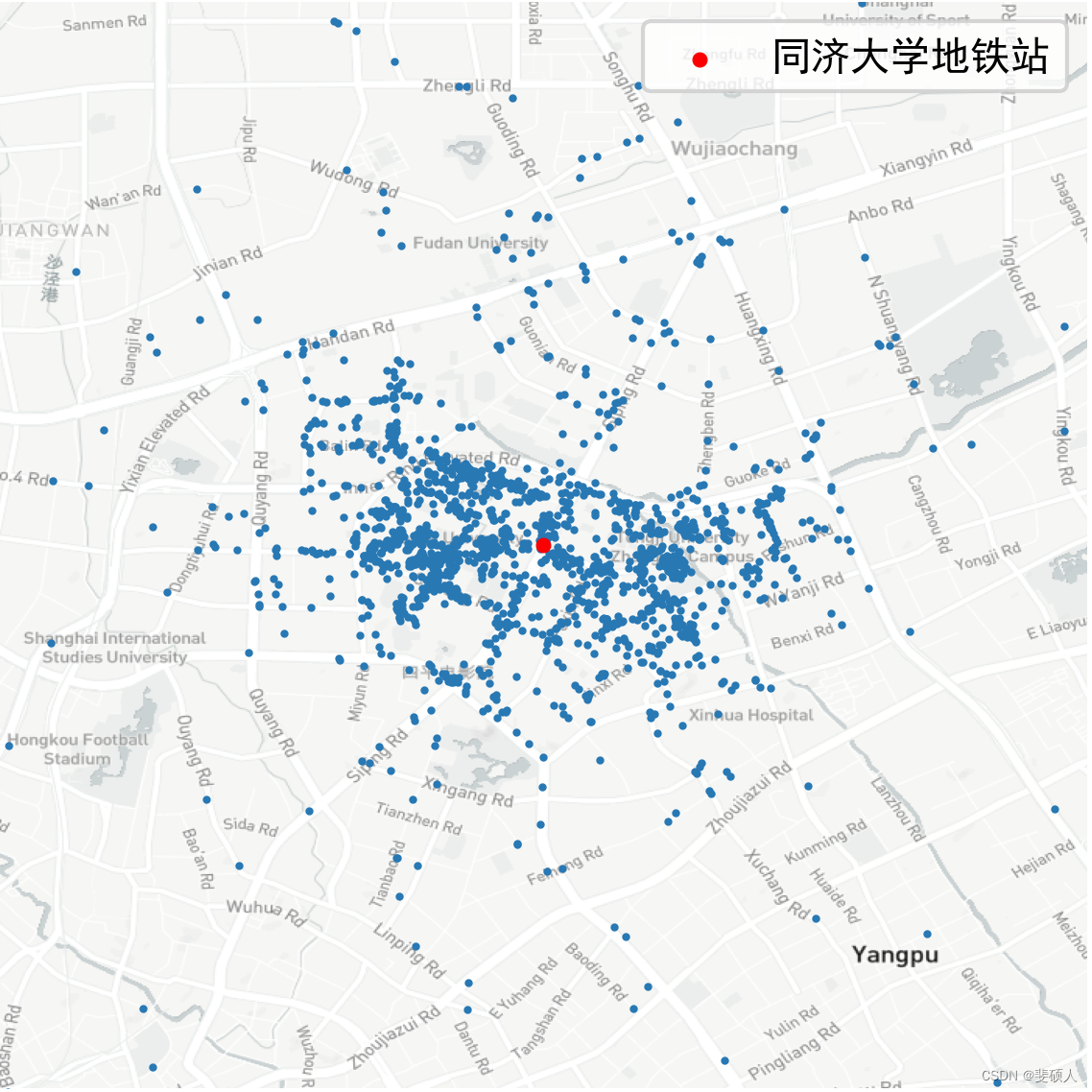
#读取轨道站点数据
metro_station = pd.read_csv(r'data/metro_station.csv')
metro_station = metro_station.drop_duplicates(subset= 'stationnames')
#提取这个站点的记录
thisstop = metro_station[metro_station['stationnames']==station]
thisstop = geopandas.GeoDataFrame(thisstop)
thisstop['geometry'] = geopandas.points_from_xy(thisstop['lon'],thisstop['lat'])
thisstop

stationnames	linename	lon	lat	geometry
同济大学	地铁10号线(新江湾城-虹桥火车站)	121.502067	31.284578	POINT (121.50207 31.28458)

#取得这个站点的位置
lon_thisstop = thisstop['lon'].iloc[0]
lat_thisstop = thisstop['lat'].iloc[0]
#确定显示范围
bounds = [lon_thisstop-0.03,lat_thisstop-0.03,lon_thisstop+0.03,lat_thisstop+0.03]

import matplotlib.pyplot as plt
fig = plt.figure(1,(6,5),dpi = 300)
ax = plt.subplot(111)
plt.sca(ax)
#加载底图
import transbigdata as tbd
#绘制底图
tbd.plot_map(plt,bounds,zoom = 14,style = 4)
points.plot(ax = ax,markersize = 1)
#标注地铁站点
thisstop.plot(ax = ax,c = 'red',markersize = 8,zorder = 2,label = station+'地铁站')
plt.legend()
#设置显示范围
plt.axis('off')
ax.set_xlim(bounds[0],bounds[2])
ax.set_ylim(bounds[1],bounds[3])
plt.show()

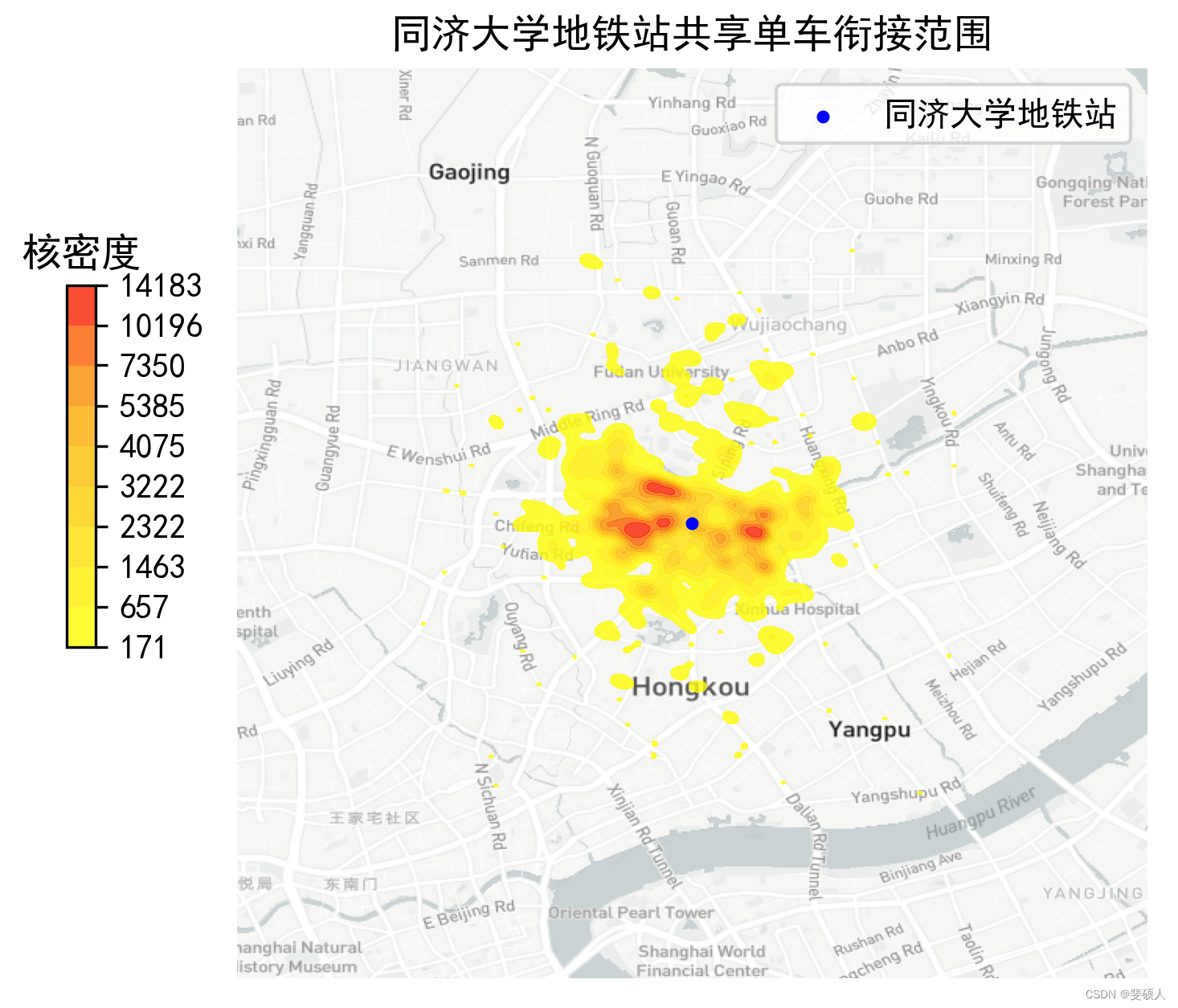
#剔除距离过远的点，否则核密度估计可能会出错
points = points[(points['lon']>bounds[0])&
(points['lat']>bounds[1])&
(points['lon']<bounds[2])&
(points['lat']<bounds[3])]

import matplotlib.pyplot as plt
fig = plt.figure(1,(6,5),dpi = 300)
ax = plt.subplot(111)
plt.sca(ax)
#加载底图
import transbigdata as tbd
bounds = [lon_thisstop-0.05,lat_thisstop-0.05,lon_thisstop+0.05,lat_thisstop+0.05]
#绘制底图
tbd.plot_map(plt,bounds,zoom = 13,style = 4)
#标注地铁站点
thisstop.plot(ax = ax,c = 'blue',markersize = 8,zorder = 2,label = station+'地铁站')
plt.legend()
#设置显示范围
plt.axis('off')
ax.set_xlim(bounds[0],bounds[2])
ax.set_ylim(bounds[1],bounds[3])
plt.title(station+'地铁站共享单车衔接范围')
#设置色标
import matplotlib
cmapname = 'autumn_r'
cmap = matplotlib.cm.get_cmap(cmapname)
cax = plt.axes([0.08, 0.4, 0.02, 0.3])
#色标的标题
plt.title('核密度')
import seaborn as sns
#绘制二维核密度图
sns.kdeplot(points['lon'],points['lat'],#指定x与y坐标所在的列
            data = points,
            alpha = 0.8,#透明度
            gridsize = 180, #绘图精细度，越高越慢
            bw = 0.1,    #高斯核大小（经纬度），越小越精细
            cmap = cmap, #定义colormap
            ax = ax, #指定绘图位置
            shade=True, #等高线间是否填充颜色
            shade_lowest=False,#最底层不显示颜色
            cbar=True, #显示colorbar
            cbar_ax=cax,#指定colorbar位置
            zorder = 1 #控制绘图顺序，使其不会挡住地铁站点
           )
plt.show()

结果保存

points[['lon','lat']].to_csv(r'data/bicycle_connection_points.csv',index = None)

bicycle_connection_points.csv

---

1. KD-Tree原理详解 ↩︎

2. 《交通时空大数据分析、挖掘与可视化（Python版）》 ↩︎