问题描述：

给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。

每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说，如果你在 nums[i] 处，你可以跳转到任意 nums[i + j] 处:

• 0 <= j <= nums[i] 
• i + j < n

返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。

示例一：

输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
     从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

示例二：

输入: nums = [2,3,0,1,4]
输出: 2

问题解决：

可以用双指针来不断表示每一个数字可以跳跃的范围，再去遍历这段范围来找到这段范围里能到达

的最远的地方，将其统计然后与数组的长度进行比较，如果小于数组长度，则继续循环，否则直接

返回步数，对应以示例一为例演示一下：

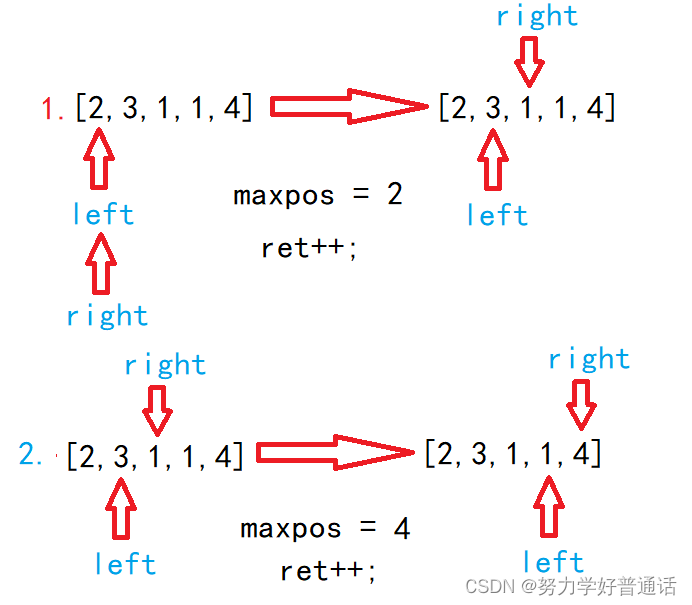
对应right和left都从0开始，通过left到right这段区间来找出最大的跳数，找到后，现将其和数组的长

度进行比较，如果小于，将left更新为right + 1，将right更新为最大跳数，同时步数++，最后在回到

找最大条数，执行循环，知道最大跳数的值大于或等于数组长度，返回步数。

代码如下：
 

class Solution {
public:
    int jump(vector<int>& nums) 
    {
        int left = 0,right = 0,maxPos = 0,ret = 0,n = nums.size();
        while(left <= right)
        {
            //判断是否已经跳到最后一个位置
            if(maxPos >= n - 1)
            {
                return ret;
            }

            for(int i = left;i <= right;i++)
            {
                maxPos = max(maxPos,nums[i] + i);
            }
            left = right + 1;
            right = maxPos;
            ret++;
        }

        return -1;
    }
};

 这就是这道题的较优的解法，时间复杂度是o(n)。