目录
一、介绍:
二、什么是 RNN 以及它与前馈神经网络有何不同:
三、RNN 背后的数学
3.1 RNN的数学方程
3.2 参数和梯度
3.2.1 损耗相对于V的梯度
3.2.2 损失相对于W的梯度
四、RNN 变体(LSTM 和 GRU)
4.1 LSTM(长短期记忆)
4.2 RNN 的实际应用:
五、最后注意事项:
一、介绍:
专家预计人工智能(AI)将致力于创造更美好的生活。他们表示,随着未来将提供更多的计算能力,即更多的图形处理单元,人工智能将为人类带来更多进步和生产力。这篇特别的文章讨论了 RNN、它的变体(LSTM、GRU)及其背后的数学。
如今,人们可以看到很多这样的人工智能应用程序,例如打击人口贩运、医疗保健顾问、自动驾驶汽车、入侵检测和预防、物体跟踪和计数、人脸检测和识别、疾病预测和人类虚拟援助。 RNN 是一种接受可变长度输入并产生可变长度输出的神经网络。它用于开发各种应用程序,例如文本到语音、聊天机器人、语言建模、情感分析、时间序列股票预测、机器翻译和名称实体识别。
文中的内容:
- 什么是 RNN 以及它与前馈神经网络有何不同
- RNN 背后的数学
- RNN 变体(LSTM 和 GRU)
- RNN 的实际应用
- 最后说明
二、什么是 RNN 以及它与前馈神经网络有何不同
RNN 是一种循环神经网络,其当前输出不仅取决于其当前值,还取决于过去的输入,而对于前馈网络,当前输出仅取决于当前输入。看看下面的例子可以更好地理解 RNN。
亚伯拉罕是以色列人文始祖。
亚伯拉罕是美国总统。
如果有人被问到谁是亚伯拉罕,他/她会说亚伯拉罕是不同的,一个来自圣经,另一个来美国总统。现在,如果将相同的任务交给机器来给出输出,则在它知道完整的上下文之前它无法说出,即预测单个单词的身份取决于了解整个上下文。此类任务可以通过 Bi-LSTM(RNN 的变体)来实现。 RNN 因其学习上下文的能力而适合此类工作。其他应用包括语音到文本转换、构建虚拟辅助、时间序列股票预测、情感分析、语言建模和机器翻译。另一方面,前馈神经网络产生的输出仅取决于当前输入。例如图像分类任务、图像分割或对象检测任务。此类网络的一种类型是卷积神经网络(CNN)。请记住,RNN 和 CNN 都是有监督的深度学习模型,即它们在训练阶段都需要标签。
三、RNN 背后的数学
3.1 RNN的数学方程
要了解 RNN 背后的数学原理,请看下图

RNN 背后的数学
正如第一个标题中所讨论的,输出取决于当前和过去的输入。令I 1为第一个输入,其维度为n*1,其中 n 是词汇表的长度。S 0是具有 d 个神经元的第一个 RNN 单元的隐藏状态。对于每个单元格,输入隐藏状态应该是前一个。对于第一个单元,用零或某个随机数初始化S 0 ,因为没有看到先前的状态。U是另一个维度为d*n的矩阵,其中d是第一个 RNN 单元中的神经元数量,n是输入词汇量大小。W是另一个矩阵,其维度为d*d。b是偏差,其维度为d*1。为了找到第一个单元的输出,采用另一个矩阵V ,其维度为k*d,其中c是维度为k*1 的偏差。
从数学上讲,第一个 RNN单元的输出如下
S 1 = UI 1 + WS 0 + b
O 1 = VS 1 +c
一般来说,
S n = UI n + WS n-1 + b
O n = VS n + c
上述方程的关键要点
一般来说,输出O n取决于S n且S n取决于S n-1。 S n-1取决于S n-2。过程一直进行到达到S 0为止。这清楚地表明第 n个时间步的输出取决于所有先前的输入。
3.2 参数和梯度
RNN 中的参数U、V、b、c、W 在所有 RNN 单元之间共享。共享的原因是创建一个可以在所有时间步上应用的通用函数。参数是可学习的,负责训练模型。在每个时间步,都会计算损失并通过梯度下降算法反向传播。
3.2.1 损耗相对于V的梯度
梯度表示切线的斜率,并指向函数增长率最大的方向。我们有兴趣找到损失最小的 V。从损失来看,它意味着成本函数或误差。简单来说,成本函数是真实值与预测值之间的差值。移动方向与相对于 V 的损失梯度方向相反。使用以下数学公式获得 V 的新数学值
![]()
其中d(L)/d(V)是从时间步长获得的所有损失的总和。有两种更新权重的方法。一种是计算定义批次的梯度然后更新它(Mini Batch)或按样本计算并更新(随机)。在计算d(L)/d(V)期间,应用链式法则。看下图来理解计算和链式法则。
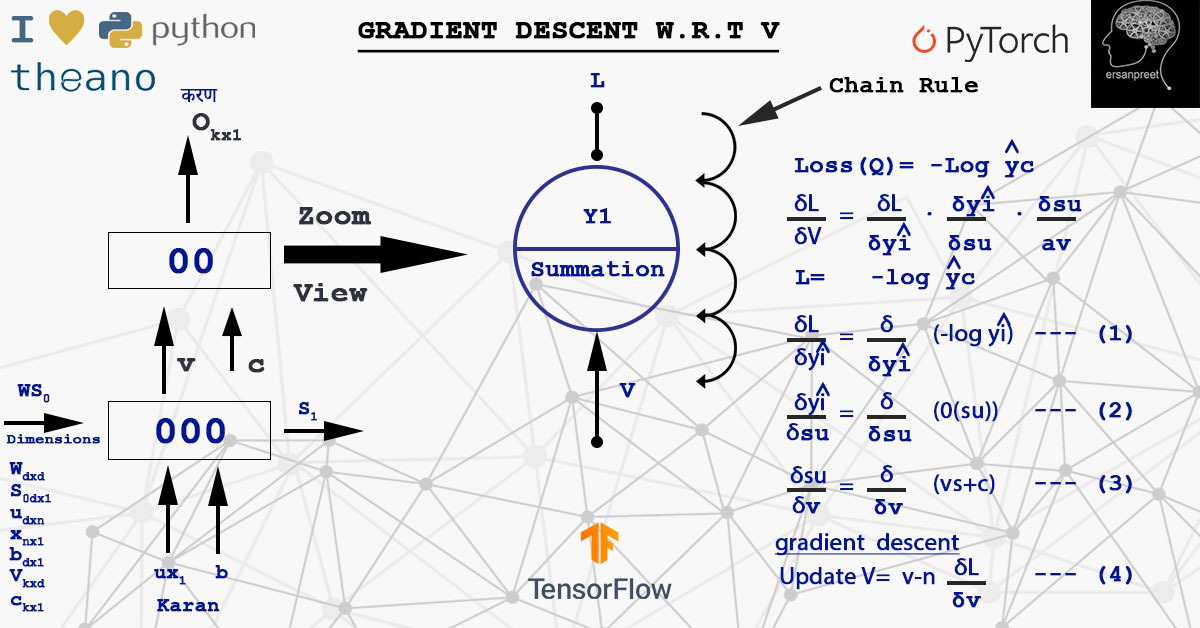
用于计算 V 损失梯度的链式规则实现
3.2.2 损失相对于W的梯度
W乘以S。为了计算任意时间步上损失相对于权重的导数,应用链式法则来考虑从S n到S 0到达W的所有路径。这意味着由于任何错误的 S n,W 都会受到影响。换句话说,一些错误的信息来自某些隐藏状态,从而导致损失。从数学上讲,权重更新如下
![]()
要记住的关键点是,梯度和权重要么在每个样本中更新,要么在批次之后更新。这取决于算法选择随机还是小批量。看一下下面的屏幕截图,以更精致的方式形象化这个概念。
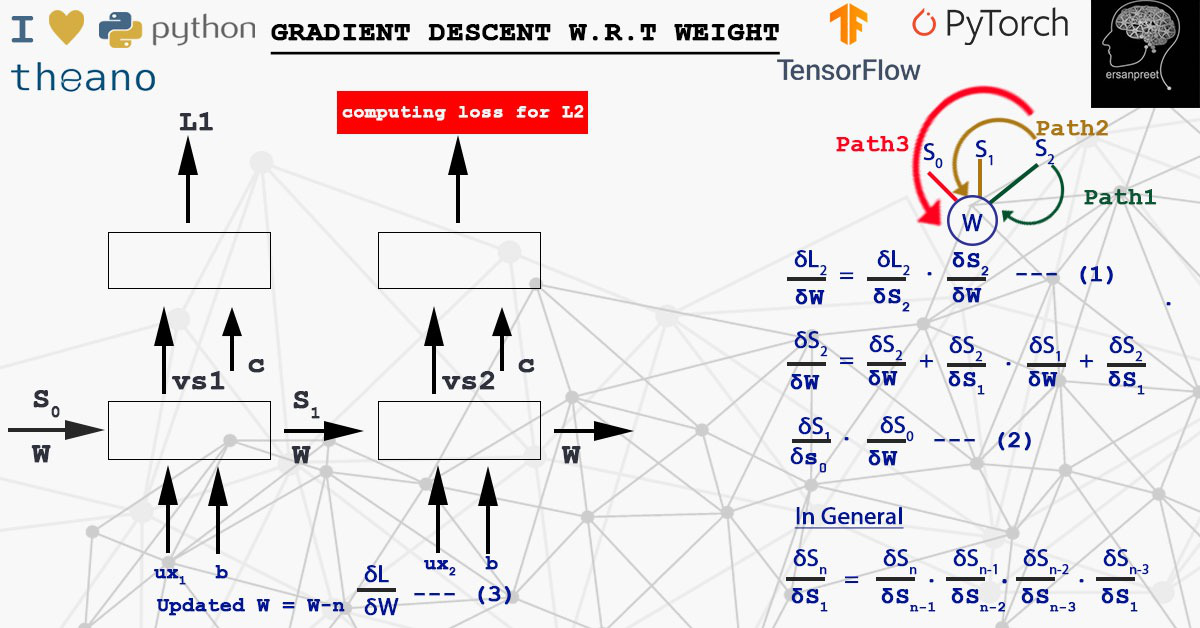
关于 W 的梯度下降
四、RNN 变体(LSTM 和 GRU)
通过上面的讨论,我希望 RNN 背后的数学原理现在已经清楚了。 RNN 的主要缺点是无论序列长度如何,状态向量的维度保持不变。考虑到一种情况,如果输入序列的长度很长,则新信息会被添加到同一状态向量中。当到达距离第一个时间步很远的第n个时间步时,信息会变得非常混乱。在这样的位置,并不清楚在时间步骤1或2提供的信息是什么。它类似于一块尺寸固定的白板,可以在上面不断地书写。在某些位置,它会变得非常混乱。人们甚至无法阅读船上写的内容。为了解决这些问题,其变体被开发为所谓的 LSTM 和 GRU。他们的工作遵循选择性阅读、写作和遗忘的原则。现在白板(类似于状态向量)是相同的,但仅在时间步写入所需的信息,并过滤掉不必要的信息,使顺序神经网络适合长序列的训练。从这里可以看出 LSTM 和 GRU 之间的区别。
4.1 LSTM(长短期记忆)
数学表示:
遵循的策略是选择性地写、读和忘记。
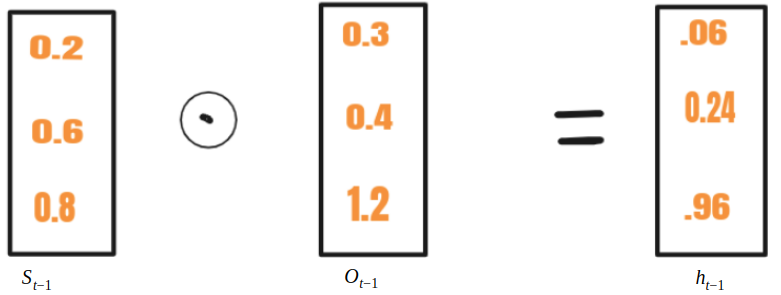
选择性写入
选择性写入:
在 RNN 中, S t- 1与x t一起输入 到单元中,而在 LSTM 中,S t-1使用另一个向量O t-1 转换为h t-1。这个过程称为选择性写入。选择性写入的数学方程如下
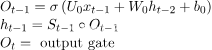
选择性阅读:
看一下下图来理解这个概念
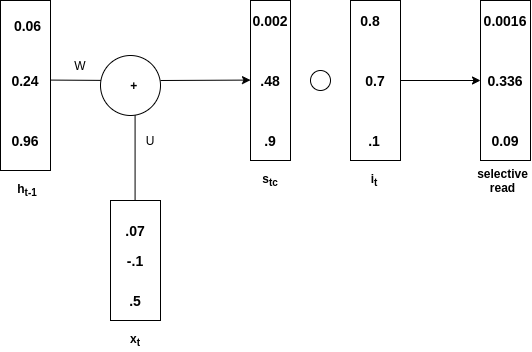
选择性阅读
h t-1与x t 相加得到 s t。然后对 (图中写为s tc )进行阿达玛积 ,得到s t。这称为输入门。只有选择性信息才会进入,这个过程称为选择性读取。从数学上讲,选择性读取的方程如下:
![]()
选择性忘记:
看一下下图来理解这个概念
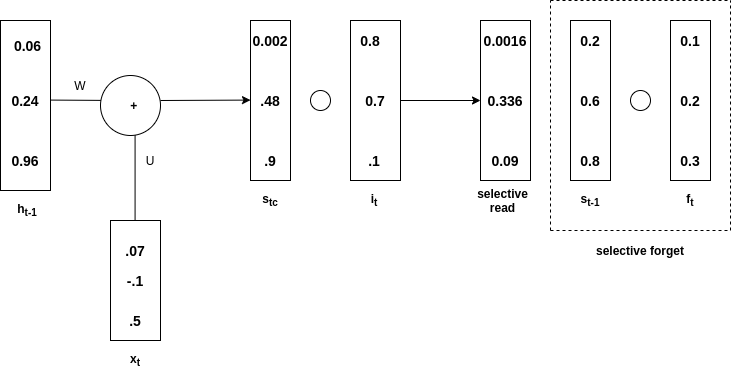
选择性遗忘
s t-1是与ft 的 阿达玛积,称为选择性遗忘。总体s t是通过选择性阅读和选择性遗忘相加得到的。请看下图来理解上面的说法
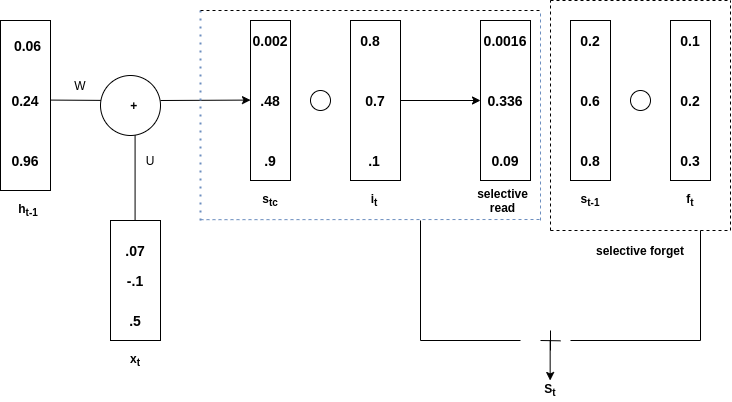
添加选择性阅读和忘记
从数学上讲,选择性遗忘的方程如下:
![]()
注意: GRU(门控循环单元)没有忘记门。它只有输入门和输出门。
4.2 RNN 的实际应用:
RNN 的用例包括语音到文本转换、构建虚拟辅助、情感分析、时间序列股票预测、机器翻译、语言建模。更多研究正在使用 RNN 及其变体创建生成式聊天机器人。其他应用程序包括图像字幕、从小段落生成大文本和文本摘要器(像 Inshorts 这样的应用程序正在使用此功能)。音乐创作和呼叫中心分析是使用 RNN 的其他领域。
五、最后注意事项:
简而言之,从开头一段就可以理解 RNN 和前馈神经网络的区别,然后深入了解 RNN 背后的数学原理。最后,通过解释 RNN 的不同变体以及 RNN 的一些实际应用来完成本文。为了研究 RNN 的应用,必须掌握微积分、导数方面的丰富知识,尤其是链式法则的工作原理。研究完理论后,应该用您最喜欢的编码语言编写有关这些主题的一些代码。