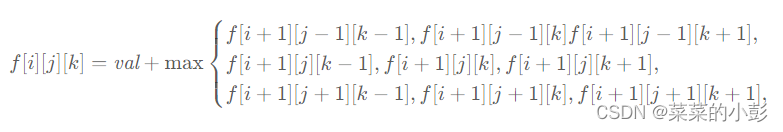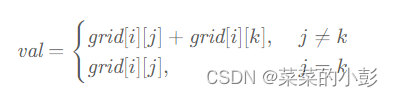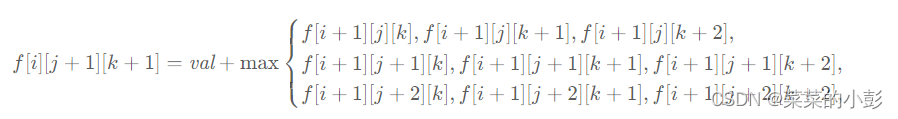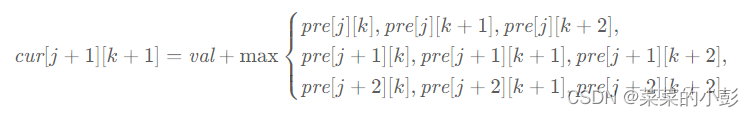2024-5-7——摘樱桃 II

news2024/12/23 0:53:03

2024-5-7

- - 题目来源
  - 我的题解
  - - 方法一记忆化搜索
    - 方法二动态规划
    - 方法三动态规划+空间优化

题目来源

力扣每日一题；题序：1463

我的题解

题解参考灵神的解析

方法一记忆化搜索

因为两个机器人是同时进行，理论上到达某一行的时间是相同的，所以对两个机器人分别使用深度优先搜索，但是需要共用统一状态，防止两个机器人走到同一位置。因为存在许多状态会重复计算，因此采用记忆化搜索，在搜索过程中记录相应的结果，后序再遇见相同状态的计算直接返回记录的结果。

时间复杂度：O( $mn^2$ )。遍历下一位置的3×3算作常量级别
空间复杂度：O( $mn^2$ )

public int cherryPickup(int[][] grid) {
    int n=grid.length;
    int m=grid[0].length;
    //memo[i][j][k]的含义  A到达（i,j）和B到达（i,k）能取得的最大樱桃数
    int[][][] memo=new int[n][m][m];
    for(int[][] r:memo){
        for(int[] t:r){
            Arrays.fill(t,-1);//表示没有计算过
        }
    }
    return dfs(0,0,m-1,grid,memo);

}
public int dfs(int i,int j,int k,int[][] grid,int[][][] memo){
    int n=grid.length;
    int m=grid[0].length;
    if(i==n||j<0||j>=m||k<0||k>=m){
        return 0;
    }
    //之前计算过
    if(memo[i][j][k]!=-1){
        return memo[i][j][k];
    }
    int res=0;
    //遍历两个机器人可以到达的位置
    for(int x=j-1;x<=j+1;x++){
        for(int y=k-1;y<=k+1;y++){
            res=Math.max(res,dfs(i+1,x,y,grid,memo));
        }
    }
    //注意判断两个机器人是否到达同一个位置
    res+=grid[i][j]+(k!=j?grid[i][k]:0);
    memo[i][j][k]=res;
    return res;
}

方法二动态规划

记忆化搜索一般情况下都能转换为动态规划。这里的动态转移方程如下：

这种定义方式没有状态能表示递归边界，即 j=−1, k=−1,这种出界的情况。因此，转移方程改为：

时间复杂度：O( $mn^2$ )。
空间复杂度：O( $mn^2$ )。

public int cherryPickup(int[][] grid) {
    int n=grid.length;
    int m=grid[0].length;
    //dp[i][j][k]的含义  A到达（i,j）和B到达（i,k）能取得的最大樱桃数
    int[][][] dp=new int[n+1][m+2][m+2];
    for(int i=n-1;i>=0;i--){
        for(int j=0;j<Math.min(m,i+1);j++){
            //从j+1开始 避免了到达同一位置
            for(int k=Math.max(j+1,m-1-i);k<m;k++){
                dp[i][j+1][k+1]=max(
                    dp[i+1][j][k],dp[i+1][j][k+1],dp[i+1][j][k+2],
                    dp[i+1][j+1][k],dp[i+1][j+1][k+1],dp[i+1][j+1][k+2],
                    dp[i+1][j+2][k],dp[i+1][j+2][k+1],dp[i+1][j+2][k+2]
                )+grid[i][j]+grid[i][k];
            }
        }
    }
    return dp[0][1][m];
}
public int max(int x,int...y){
    for(int t:y){
        x=Math.max(x,t);
    }
    return x;
}

方法三动态规划+空间优化

上面的状态转移方程，在计算 f[i]时，只会用到 f[i+1]，不会用到 >i+1 的状态。
可以用两个二维数组滚动计算，用 cur 表示 f[i]，pre 表示 f[i+1]，状态转移方程改为

从 i 枚举到 i−1 之前，交换 cur和 pre，相当于把 cur 变成对 i−1 而言的 pre。

时间复杂度：O( $mn^2$ )。遍历下一位置的3×3算作常量级别
空间复杂度：O( $n^2$ )

public int cherryPickup(int[][] grid) {
    int n=grid.length;
    int m=grid[0].length;
    //dp[i][j][k]的含义  A到达（i,j）和B到达（i,k）能取得的最大樱桃数
    int[][] preDp=new int[m+2][m+2];
    int[][] curDp=new int[m+2][m+2];
    for(int i=n-1;i>=0;i--){
        for(int j=0;j<Math.min(m,i+1);j++){
            //从j+1开始 避免了到达同一位置
            for(int k=Math.max(j+1,m-1-i);k<m;k++){
                curDp[j+1][k+1]=max(
                    preDp[j][k],preDp[j][k+1],preDp[j][k+2],
                    preDp[j+1][k],preDp[j+1][k+1],preDp[j+1][k+2],
                    preDp[j+2][k],preDp[j+2][k+1],preDp[j+2][k+2]
                )+grid[i][j]+grid[i][k];
            }
        }
        int[][] t=preDp;
        preDp=curDp;
        curDp=t;
    }
    return preDp[1][m];
}
public int max(int x,int...y){
    for(int t:y){
        x=Math.max(x,t);
    }
    return x;
}