map、set底层封装模拟实现（红黑树）

news2024/12/28 7:31:30

文章目录

    • 一、红黑树
      • 1.1红黑树的规则：
      • 1.2红黑树的插入操作
        • 1.2.1不需要旋转（如果叔叔存在且为红,这里的C表示孩子，P表示父亲，U表示叔叔，G表示祖父），包含四种情况，无论孩子在哪里，都是只需要改变叔叔和父亲的颜色为黑，祖父为红，然后向上继续走，C = G
        • 1.2.2需要旋转（左旋，右旋，左右双旋，右左双旋），叔叔不存在或者为黑
      • 1.2红黑树的插入代码
      • 1.3红黑树的整体框架
    • 二、map、set的底层封装
      • 2.1set的底层封装
      • 2.2map的底层封装
      • 2.3红黑树的底层封装

一、红黑树

相较于前面的AVL树，红黑树的优势是：旋转次数减少，效率提高了，同时还保留了AVL树的查找优势

1.1红黑树的规则：

1.每个节点不是红色就是黑色
2.红色节点的孩子一定是黑色节点
3.不能有连续的红色节点
4.每条路径（走到空为止）上的黑色节点数量相同
5.最短路径<=最长路径<=2最短路径（当某条路径只有黑色节点，而另一条路径红色节点数量和黑色节点相同，那么最长路径就是最短路路径的两倍）

1.2红黑树的插入操作

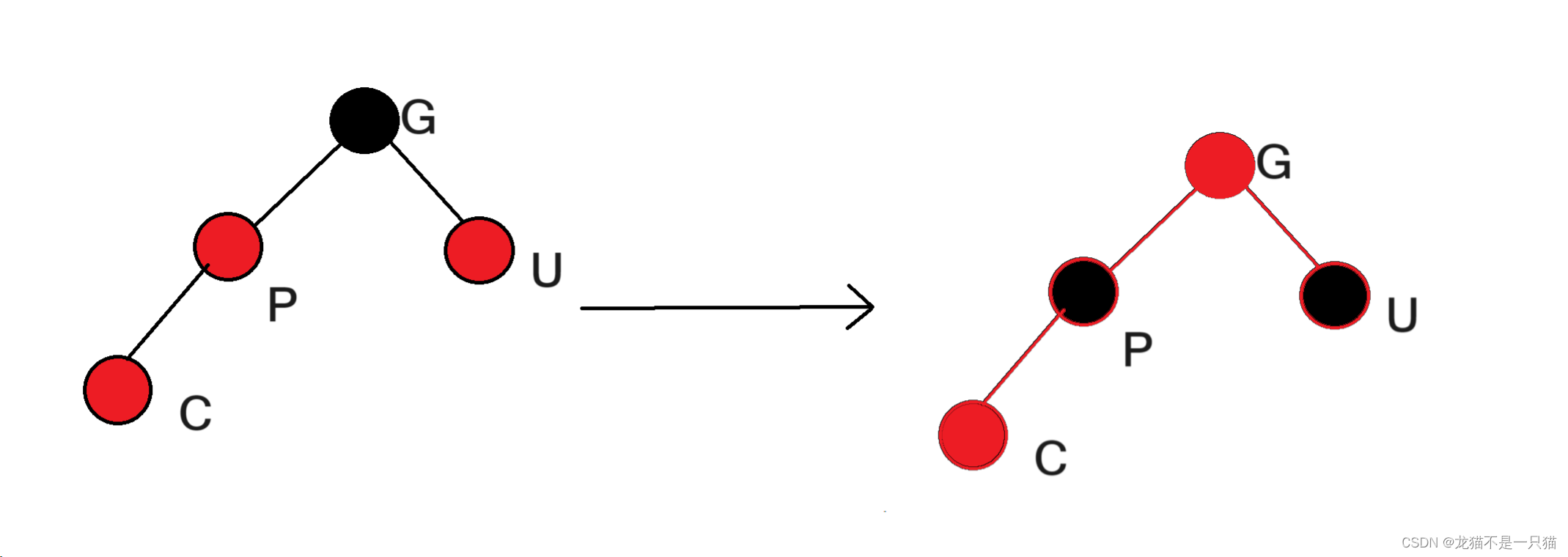
1.2.1不需要旋转（如果叔叔存在且为红,这里的C表示孩子，P表示父亲，U表示叔叔，G表示祖父），包含四种情况，无论孩子在哪里，都是只需要改变叔叔和父亲的颜色为黑，祖父为红，然后向上继续走，C = G

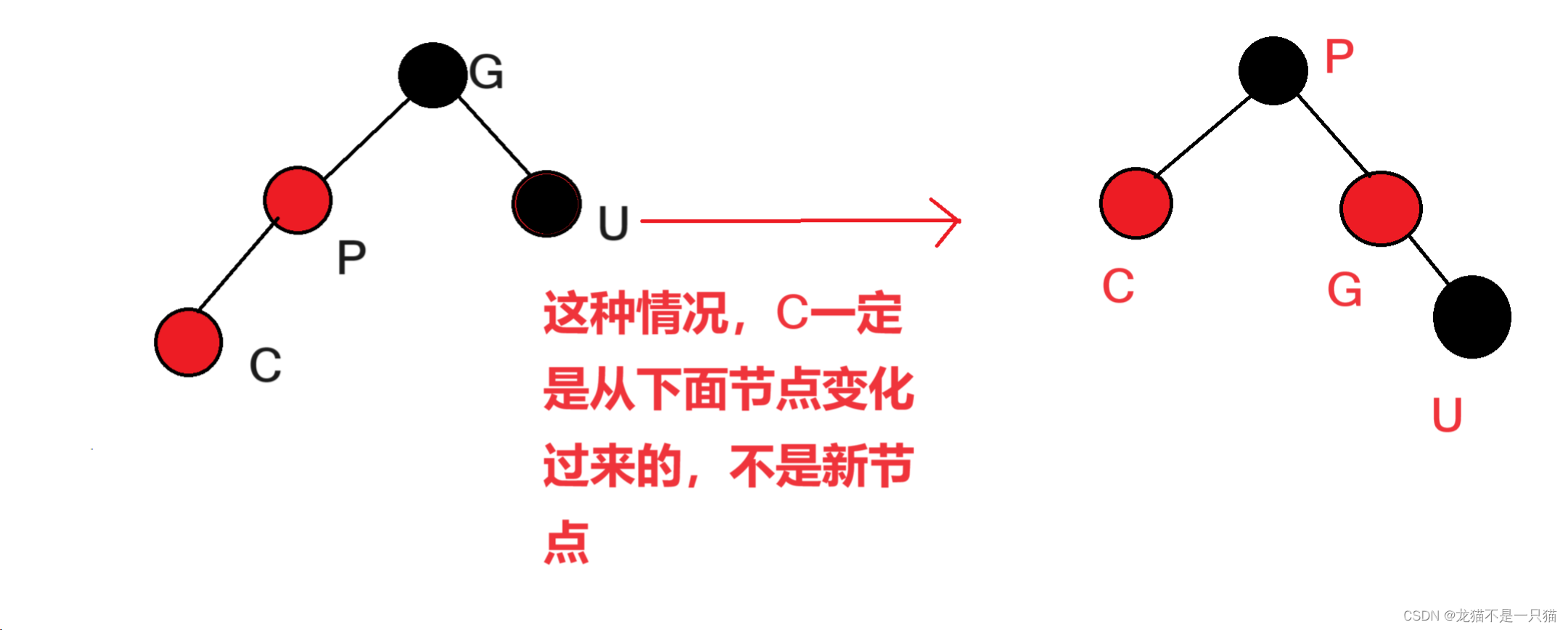
在这里插入图片描述

1.2.2需要旋转（左旋，右旋，左右双旋，右左双旋），叔叔不存在或者为黑

右旋的情况(这里省略了C,P,U所连的节点）

在这里插入图片描述
左右双旋的情况(这里省略了C,P,U所连的节点）
在这里插入图片描述
下面两种情况省略

1.2红黑树的插入代码

	bool Insert(const pair<K, V>& data)
	{
		if (_root == nullptr)
		{
			_root = new Node(data);
			_root->_col = BLACK;
			return true;
		}

		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{
			if (data.first > cur->_data.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (data.first < cur->_data.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
				return false;
		}

		cur = new Node(data);
		if (parent->_data.first > cur->_data.first)
			parent->_left = cur;
		else
			parent->_right = cur;

		cur->_parent = parent;

		//判断父亲是否为红，为黑就不管
		while (parent && parent->_col == RED)
		{
			Node* grandfather = parent->_parent;
			if (parent == grandfather->_left)
			{
				Node* uncle = grandfather->_right;
				if (uncle && uncle->_col == RED)//叔叔存在且为红
				{
					uncle->_col = parent->_col = BLACK;
					grandfather->_col = RED;
					cur = grandfather;//继续向上处理
					parent = cur->_parent;
				}
				else
				{
					if (cur == parent->_left)
					{
						//叔叔为黑或者叔叔不存在
						RotateR(grandfather);
						parent->_col = BLACK;
						grandfather->_col = RED;
					}
					else
					{
						RotateL(parent);
						RotateR(grandfather);
						cur->_col = BLACK;
						parent->_col = RED;
					}
					break;
				}
			}
			else
			{
				Node* uncle = grandfather->_left;
				if (uncle && uncle->_col == RED)
				{
					uncle->_col = parent->_col = BLACK;
					grandfather->_col = RED;
					cur = grandfather;//继续向上处理
					parent = cur->_parent;
				}
				else
				{
					if (cur == parent->_right)
					{
						RotateL(grandfather);
						parent->_col = BLACK;
						grandfather->_col = RED;
					}
					else
					{
						RotateR(parent);
						RotateL(grandfather);
						cur->_col = BLACK;
						grandfather->_col = RED;
					}
					break;
				}
			}
		}
		_root->_col = BLACK;
		return true;
	}
	void RotateL(Node* parent)
{
	Node* subR = parent->_right;
	Node* subRL = subR->_left;

	parent->_right = subRL;
	if (subRL)
		subRL->_parent = parent;

	Node* ppnode = parent->_parent;

	subR->_left = parent;
	parent->_parent = subR;

	if (ppnode == nullptr)
	{
		_root = subR;
		_root->_parent = nullptr;
	}
	else
	{
		if (ppnode->_left == parent)
		{
			ppnode->_left = subR;
		}
		else
		{
			ppnode->_right = subR;
		}

		subR->_parent = ppnode;
	}
}

void RotateR(Node* parent)
{
	Node* subL = parent->_left;
	Node* subLR = subL->_right;

	parent->_left = subLR;
	if (subLR)
		subLR->_parent = parent;

	Node* ppnode = parent->_parent;

	subL->_right = parent;
	parent->_parent = subL;

	if (parent == _root)
	{
		_root = subL;
		_root->_parent = nullptr;
	}
	else
	{
		if (ppnode->_left == parent)
		{
			ppnode->_left = subL;
		}
		else
		{
			ppnode->_right = subL;
		}
		subL->_parent = ppnode;
	}
}

1.3红黑树的整体框架

#pragma once
#include<iostream>
#include<assert.h>
using namespace std;

//颜色定义
enum color
{
	RED,
	BLACK
};

template<class K,class V>
struct RBTreeNode
{
	typedef RBTreeNode<K, V> Node;
	pair<K, V> _data;
	Node* _left;
	Node* _right;
	Node* _parent;
	color _col;

	//构造函数
	RBTreeNode(const pair<K, V>& data)
		:_left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _col(RED)
		, _data(data)
	{}
};


template<class K,class V>
class RBTree
{
public:
	typedef RBTreeNode<K, V> Node;
	bool Insert(const pair<K, V>& data)
	{
		if (_root == nullptr)
		{
			_root = new Node(data);
			_root->_col = BLACK;
			return true;
		}

		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{
			if (data.first > cur->_data.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (data.first < cur->_data.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
				return false;
		}

		cur = new Node(data);
		if (parent->_data.first > cur->_data.first)
			parent->_left = cur;
		else
			parent->_right = cur;

		cur->_parent = parent;

		//判断父亲是否为红，为黑就不管
		while (parent && parent->_col == RED)
		{
			Node* grandfather = parent->_parent;
			if (parent == grandfather->_left)
			{
				Node* uncle = grandfather->_right;
				if (uncle && uncle->_col == RED)//叔叔存在且为红
				{
					uncle->_col = parent->_col = BLACK;
					grandfather->_col = RED;
					cur = grandfather;//继续向上处理
					parent = cur->_parent;
				}
				else
				{
					if (cur == parent->_left)
					{
						//叔叔为黑或者叔叔不存在
						RotateR(grandfather);
						parent->_col = BLACK;
						grandfather->_col = RED;
					}
					else
					{
						RotateL(parent);
						RotateR(grandfather);
						cur->_col = BLACK;
						parent->_col = RED;
					}
					break;
				}
			}
			else
			{
				Node* uncle = grandfather->_left;
				if (uncle && uncle->_col == RED)
				{
					uncle->_col = parent->_col = BLACK;
					grandfather->_col = RED;
					cur = grandfather;//继续向上处理
					parent = cur->_parent;
				}
				else
				{
					if (cur == parent->_right)
					{
						RotateL(grandfather);
						parent->_col = BLACK;
						grandfather->_col = RED;
					}
					else
					{
						RotateR(parent);
						RotateL(grandfather);
						cur->_col = BLACK;
						grandfather->_col = RED;
					}
					break;
				}
			}
		}
		_root->_col = BLACK;
		return true;
	}

	void Inorder()
	{
		_Inorder(_root);
	}

private:
	void _Inorder(Node* root)
	{
		if (root == nullptr)
			return;
		_Inorder(root->_left);
		cout << root->_data.first << endl;
		_Inorder(root->_right);
	}
	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;

		parent->_right = subRL;
		if (subRL)
			subRL->_parent = parent;

		Node* ppnode = parent->_parent;

		subR->_left = parent;
		parent->_parent = subR;

		if (ppnode == nullptr)
		{
			_root = subR;
			_root->_parent = nullptr;
		}
		else
		{
			if (ppnode->_left == parent)
			{
				ppnode->_left = subR;
			}
			else
			{
				ppnode->_right = subR;
			}

			subR->_parent = ppnode;
		}
	}

	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;

		parent->_left = subLR;
		if (subLR)
			subLR->_parent = parent;

		Node* ppnode = parent->_parent;

		subL->_right = parent;
		parent->_parent = subL;

		if (parent == _root)
		{
			_root = subL;
			_root->_parent = nullptr;
		}
		else
		{
			if (ppnode->_left == parent)
			{
				ppnode->_left = subL;
			}
			else
			{
				ppnode->_right = subL;
			}
			subL->_parent = ppnode;
		}
	}

	Node* _root = nullptr;
};

二、map、set的底层封装

这里我们需要加上迭代器和仿函数（为了套用同一个红黑树的模版）
map有两个模版参数、set只有一个模版参数，因此我们需要加一个仿函数来确定是map还是set

2.1set的底层封装

namespace SF
{
	//仿函数
	template<class K>
	class set
	{
		struct SetKeyOfT
		{
			const K& operator()(const K& key)
			{
				return key;
			}
		};
	public:
		typedef typename RBTree<K,const K, SetKeyOfT>::iterator iterator;
		iterator begin()
		{
			return _t.begin();
		}

		iterator end()
		{
			return _t.end();
		}

		bool insert(const K& key)
		{
			return _t.Insert(key);
		}

	private:
		RBTree<K,const K, SetKeyOfT> _t;

	};
}

2.2map的底层封装

namespace SF
{
	template<class K,class V> 
	class map
	{
		struct MapKeyOfT
		{
			const K& operator()(const pair<K,V>& kv)
			{
				return kv.first;
			}
		};
	public:
		typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::iterator iterator;

		iterator begin()
		{
			return _t.begin();
		}

		iterator end()
		{
			return _t.end();
		}

		bool insert(const pair<K,V>& data)
		{
			return _t.Insert(data);
		}
	private:
		RBTree<K, pair<const K, V>, MapKeyOfT> _t;
	};
}

2.3红黑树的底层封装

#pragma once
#include<vector>

enum Colour
{
	RED,
	BLACK
};

template<class T>
struct RBTreeNode
{
	RBTreeNode<T>* _left;
	RBTreeNode<T>* _right;
	RBTreeNode<T>* _parent;
	Colour _col;
	T _data;

	RBTreeNode(const T& data)
		:_left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _data(data)
		, _col(RED)
	{}
};


template<class T>
struct RBTreeIterator
{
	typedef RBTreeNode<T> Node;
	typedef RBTreeIterator<T> Self;

	Node* _node;

	RBTreeIterator(Node* node)
		:_node(node)
	{}

	T& operator*()
	{
		return _node->_data;
	}

	T* operator->()
	{
		return &_node->_data;
	}

	Self& operator++()
	{
		if (_node->_right)
		{
			// 右子树的中序第一个(最左节点)
			Node* subLeft = _node->_right;
			while (subLeft->_left)
			{
				subLeft = subLeft->_left;
			}

			_node = subLeft;
		}
		else
		{
			// 祖先里面孩子是父亲左的那个
			Node* cur = _node;
			Node* parent = cur->_parent;
			while (parent && cur == parent->_right)
			{
				cur = parent;
				parent = cur->_parent;
			}

			_node = parent;
		}

		return *this;
	}

	Self& operator--()
	{
		// 
		return *this;
	}

	bool operator!=(const Self& s)
	{
		return _node != s._node;
	}

	bool operator== (const Self & s)
	{
		return _node == s._node;
	}
};

// set->RBTree<K, K, SetKeyOfT>
// map->RBTree<K, pair<K, V>, MapKeyOfT>

// KeyOfT仿函数 取出T对象中的key
template<class K, class T, class KeyOfT>
class RBTree
{
	typedef RBTreeNode<T> Node;
public:
	typedef RBTreeIterator<T> iterator;

	iterator begin()
	{
		Node* subLeft = _root;
		while (subLeft && subLeft->_left)
		{
			subLeft = subLeft->_left;
		}

		return iterator(subLeft);
	}

	iterator end()
	{
		return iterator(nullptr);
	}

	bool Insert(const T& data)
	{
		if (_root == nullptr)
		{
			_root = new Node(data);
			_root->_col = BLACK;
			return true;
		}

		KeyOfT kot;
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (kot(cur->_data) < kot(data))
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (kot(cur->_data) > kot(data))
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}

		cur = new Node(data); // 红色的
		if (kot(parent->_data) < kot(data))
		{
			parent->_right = cur;
		}
		else
		{
			parent->_left = cur;
		}
		cur->_parent = parent;

		while (parent && parent->_col == RED)
		{
			Node* grandfather = parent->_parent;
			if (parent == grandfather->_left)
			{
				Node* uncle = grandfather->_right;
				// 情况一：叔叔存在且为红
				if (uncle && uncle->_col == RED)
				{
					// 变色
					parent->_col = uncle->_col = BLACK;
					grandfather->_col = RED;

					// 继续往上处理
					cur = grandfather;
					parent = cur->_parent;
				}
				else
				{
					// 情况二：叔叔不存在或者存在且为黑
					// 旋转+变色
					if (cur == parent->_left)
					{
						//       g
						//    p    u
						// c
						RotateR(grandfather);
						parent->_col = BLACK;
						grandfather->_col = RED;
					}
					else
					{
						//       g
						//    p     u
						//      c
						RotateL(parent);
						RotateR(grandfather);
						cur->_col = BLACK;
						grandfather->_col = RED;
					}

					break;
				}
			}
			else
			{
				Node* uncle = grandfather->_left;
				// 情况一：叔叔存在且为红
				if (uncle && uncle->_col == RED)
				{
					// 变色
					parent->_col = uncle->_col = BLACK;
					grandfather->_col = RED;

					// 继续往上处理
					cur = grandfather;
					parent = cur->_parent;
				}
				else
				{
					// 情况二：叔叔不存在或者存在且为黑
					// 旋转+变色
					//      g
					//   u     p
					//            c
					if (cur == parent->_right)
					{
						RotateL(grandfather);
						parent->_col = BLACK;
						grandfather->_col = RED;
					}
					else
					{
						//		g
						//   u     p
						//      c
						RotateR(parent);
						RotateL(grandfather);
						cur->_col = BLACK;
						grandfather->_col = RED;
					}

					break;
				}
			}
		}

		_root->_col = BLACK;

		return true;
	}

	void RotateL(Node* parent)
	{

		Node* subR = parent->_right;
		Node* subRL = subR->_left;

		parent->_right = subRL;
		if (subRL)
			subRL->_parent = parent;

		subR->_left = parent;
		Node* ppnode = parent->_parent;
		parent->_parent = subR;

		if (parent == _root)
		{
			_root = subR;
			subR->_parent = nullptr;
		}
		else
		{
			if (ppnode->_left == parent)
			{
				ppnode->_left = subR;
			}
			else
			{
				ppnode->_right = subR;
			}
			subR->_parent = ppnode;
		}
	}

	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;

		parent->_left = subLR;
		if (subLR)
			subLR->_parent = parent;

		subL->_right = parent;

		Node* ppnode = parent->_parent;
		parent->_parent = subL;

		if (parent == _root)
		{
			_root = subL;
			subL->_parent = nullptr;
		}
		else
		{
			if (ppnode->_left == parent)
			{
				ppnode->_left = subL;
			}
			else
			{
				ppnode->_right = subL;
			}
			subL->_parent = ppnode;
		}
	}

private:
	Node* _root = nullptr;
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1647785.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

复杂事件处理（CEP）引擎白皮书正式发布！

复杂事件处理（CEP）引擎白皮书正式发布！

流数据是一种持续实时生成且动态变化的时间序列数据&#xff0c;涵盖了金融交易、物联网&#xff08;IoT&#xff09;传感器采集、物流运营、零售订单等各类持续生成动态数据的场景。 传统的流计算引擎能够高效地处理单一结构的数据流&#xff0c;不能应对需要识别数据流中的事…
阅读更多...
VMware虚拟网卡网络适配器出现黄色感叹号

VMware虚拟网卡网络适配器出现黄色感叹号

问题发生&#xff1a;VMware在使用Ubuntu的过程中突然卡死&#xff0c;强制关闭开启后就发生了网络无法连接 找到电脑的设备管理发现VMware的适配器出现黄色感叹号 解决方法&#xff1a; 下载软件ccleaner 扫描问题&#xff0c;懒得去找就修复了所有的问题 最后发现适配器…
阅读更多...
jenkins+gitlab+ansible-tower实现发布

jenkins+gitlab+ansible-tower实现发布

前提准备&#xff1a; gitlab中上传相应的jenkinsfile文件和源码。 安装和破解ansible-tower。 安装jenkins。 大致流程&#xff1a;从gitlab中拉取文件&#xff0c;存放到windows机器上&#xff0c;使用nuget等进行打包到windows中&#xff0c;使用sshPublisher语句传输到远程…
阅读更多...
JVM调参实践总结

JVM调参实践总结

JVM调优–理论篇从理论层面介绍了如何对JVM调优。这里再写一篇WIKI&#xff0c;尝试记录下JVM参数使用的最佳实践&#xff0c;注意&#xff0c;这里重点介绍HotSpot VM的调参&#xff0c;其他JVM的调参可以类比&#xff0c;但不可照搬。 Java版本选择 基于Java开发应用时&…
阅读更多...
深度学习之基于Matlab特征匹配的手写电话号码、数字识别系统

深度学习之基于Matlab特征匹配的手写电话号码、数字识别系统

欢迎大家点赞、收藏、关注、评论啦 &#xff0c;由于篇幅有限&#xff0c;只展示了部分核心代码。 文章目录 一项目简介 二、功能三、系统四. 总结 一项目简介 一、项目背景 在信息化日益发展的今天&#xff0c;手写电话号码和数字的识别技术显得尤为重要。这种技术不仅能够提…
阅读更多...
mysql 离线安装

mysql 离线安装

package download mysql https://dev.mysql.com/downloads/mysql/ libaio http://mirror.centos.org/centos/7/os/x86_64/Packages/libaio-0.3.109-13.el7.x86_64.rpm 根据自己服务器选择下载对应的安装包及依赖 删除本机自带mysql相关 # 首先排查服务器自身是否有安装对应m…
阅读更多...
实时Linux对EtherCAT工业自动化协议的支持

实时Linux对EtherCAT工业自动化协议的支持

在自动化技术和工业控制领域&#xff0c;实时通信网络的重要性不断增长。EtherCAT&#xff08;Ethernet for Control Automation Technology&#xff09;作为一种高效的工业以太网通信协议&#xff0c;因其出色的性能和灵活性而广受欢迎。而实时Linux作为影响最为广泛的开源实时…
阅读更多...
英码科技推出昇腾系列AI加速卡：专为视频解析与模型推理场景打造，更具成本竞争力！

英码科技推出昇腾系列AI加速卡：专为视频解析与模型推理场景打造，更具成本竞争力！

当前&#xff0c;人工智能的发展已进入加速渗透千行百业的阶段&#xff0c;算力已然成为数字化转型关键的新质生产力。随着国际挑战的加剧&#xff0c;国产算力的发展趋势愈发明显&#xff0c;市场需求也呈现出激增的态势。在这一大背景下&#xff0c;华为昇腾以其强大的技术实…
阅读更多...
字节人都用的婚恋交友相亲平台有哪些？聊聊互联网大厂的人是怎么脱单的！

字节人都用的婚恋交友相亲平台有哪些？聊聊互联网大厂的人是怎么脱单的！

虽然在字节这样的公司上班&#xff0c;也算是人中之人了。但是也耐不住29岁了&#xff0c;快成大龄剩女了。迫于长辈的催婚压力&#xff0c;所以带着任务体验了一遍各大相亲交友平台&#xff0c;以下是我的使用感受。 1、青藤之恋&#xff1a;偏相亲定位&#xff0c;曾经高学历…
阅读更多...
使用socat 做端口转发 调试设备

使用socat 做端口转发 调试设备

使用 socat 监听设备的端口&#xff0c;转发到PC的 一个sniff 程序上&#xff0c;查看wireshark 或者直接用 scapy 进行分析 有了socat 也可以做 nat 映射
阅读更多...
【Redis分布式缓存】 哨兵机制

【Redis分布式缓存】 哨兵机制

Redis 哨兵机制 哨兵作用和原理 Redis提供了哨兵&#xff08;Sentinel&#xff09;机制来实现主从集群的自动故障恢复。 哨兵的作用 监控&#xff1a;Sentinel 会不断检查您的master和slave是否按预期工作自动故障恢复&#xff1a;如果master故障&#xff0c;Sentinel会将一…
阅读更多...
js中的复制粘贴（亲测有效）

js中的复制粘贴（亲测有效）

下方微信公众号 和微信小程序推荐 js中的复制粘贴 navigator.clipboard.writeText(copyText) 是 Web API 中的一个方法&#xff0c;用于将指定的文本内容复制到用户的剪贴板。这个方法属于 Clipboard API&#xff0c;它使得网页能够读取和写入剪贴板的内容。 具体来说&#…
阅读更多...
JSP合同信息管理系统参考论文（论文 + 源码）

JSP合同信息管理系统参考论文（论文 + 源码）

【免费】JSP合同信息管理系统.zip资源-CSDN文库https://download.csdn.net/download/JW_559/89273651JSP合同信息管理系统 摘要 随着信息科学技术的飞速发展&#xff0c;人们逐渐意识到对信息管理软件的运用可以使日常工作更加方便、快捷和高效。论文详细论述了公司合同管理系…
阅读更多...
28 JavaScript学习： 代码规范

28 JavaScript学习： 代码规范

代码规范通常包括以下几个方面: 变量和函数的命名规则空格&#xff0c;缩进&#xff0c;注释的使用规则。其他常用规范…… 变量名 在编写JavaScript代码时&#xff0c;遵守良好的变量命名规范是非常重要的&#xff0c;这可以增加代码的可读性和可维护性。以下是一些常见的…
阅读更多...
高频次的低价监测如何实现

高频次的低价监测如何实现

品牌在做控价的过程中&#xff0c;需要对渠道中的低价数据进行监测&#xff0c;但价格数据变化快&#xff0c;涉及的促销信息也很多&#xff0c;如何将这些变化的数据监测到位&#xff0c;同时对于低价的凭证还要截图留证&#xff0c;以便有效的进行渠道治理&#xff0c;这就需…
阅读更多...
【算法练级js+java】重复给定字符n次

【算法练级js+java】重复给定字符n次

题目 Repeats the given string n times.&#xff08;复制指定的字符串n次&#xff09; 期望结果 /** * Repeats the given string n times. * * repeat(‘, 3) * // > **’ * * repeat(‘abc’, 2) * // > ‘abcabc’ * * repeat(‘abc’, 0) * // > “” **/ 代码…
阅读更多...
LLaMA 羊驼系大语言模型的前世今生

LLaMA 羊驼系大语言模型的前世今生

关于 LLaMA LLaMA是由Meta AI发布的大语言系列模型&#xff0c;完整的名字是Large Language Model Meta AI&#xff0c;直译&#xff1a;大语言模型元AI。Llama这个单词本身是指美洲大羊驼&#xff0c;所以社区也将这个系列的模型昵称为羊驼系模型。 Llama、Llama2 和 Llama3…
阅读更多...
快速入门Jmeter5.X 性能测试小白到高手这一篇就够了

快速入门Jmeter5.X 性能测试小白到高手这一篇就够了

&#x1f680; 作者 &#xff1a;“二当家-小 D” &#x1f680; 博主简介&#xff1a;⭐前荔枝 FM 架构师、阿里资深工程师||曾任职于阿里巴巴担任多个项目负责人&#xff0c;8 年开发架构经验&#xff0c;精通 java, 擅长分布式高并发架构, 自动化压力测试&#xff0c;微服务…
阅读更多...
如何使git提交的时候忽略一些特殊文件？

如何使git提交的时候忽略一些特殊文件？

认识.gitignore文件 在生成远程仓库的时候我们会看到这样一个选项&#xff1a; 这个.gitignore文件有啥用呢&#xff1f; .gotignore文件是Git版本控制系统中的一个特殊文件。用来指定哪些文件或者目录不被Git追踪或者提交到版本库中。也就意味着&#xff0c;如果我们有一些文…
阅读更多...
Android build.prop生成过程源码分析

Android build.prop生成过程源码分析

Android的build.prop文件是在Android编译时刻收集的各种property【LCD density/语言/编译时间, etc.】&#xff1b;编译完成之后&#xff0c;文件生成在out/target/product/<board【OK1000】>/system/目录下&#xff1b;在Android运行时刻可以通过property_get()[c/c域] …
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023