PS:每每温故必而知新
什么是神经网络?
- 一、一个单神经元的神经网络
- 二、多个单神经元的神经网络
- 三、到底什么是机器学习?(重点)
- 1:什么是机器学习的训练?
- 2:什么是模型?权重 W W W和偏差 b b b又是什么?
- 3:神经元的里面是什么?
- 神经元里的基础函数:线性变换函数
- 神经元里为了多样化任务的函数:激活函数
- 四、损失函数和代价函数
- 1.标签和预测
- 2.损失函数
- 3.代价函数
- ?、什么是深度学习?
一、一个单神经元的神经网络
深度学习中的神经网络是一种受人脑结构启发的算法模型,主要用于模拟人脑处理和学习信息的方式。这种网络包括多层的 “神经元” 节点。
每个节点都是一个计算单元,它们通过层与层之间的连接互相传递信息。
每个连接都有一个权重,这些权重在学习过程中会不断更新,以帮助网络更好地完成特定任务,如图像识别、语音理解或文本翻译。
神经网络的基本组成包括:
- 输入层:接收原始数据输入,如图像的像素值、音频信号或文本数据。
- 隐藏层:一个或多个,负责从输入中提取特征。每个隐藏层都会将前一层的输出作为输入,通过激活函数进一步处理这些数据。
- 输出层:生成最终的输出,如分类任务中的类别标签。
举个简单的例子:我们希望预测房间大小和房价之间的关系。
假设我们有6个房价变化和房间大小变化的数据,我们把它们放在一个直角坐标系上。

我们希望通过六个数据的信息,找到一个 “房间大小和房价的关系函数”。
当我们获得这个 “函数” ,我们只需要输入 房间大小 就可以计算出对应的 房价 。
对于这个简单的任务,函数即是初始为0的一个线性回归函数(X轴为房间大小,Y为价格)。
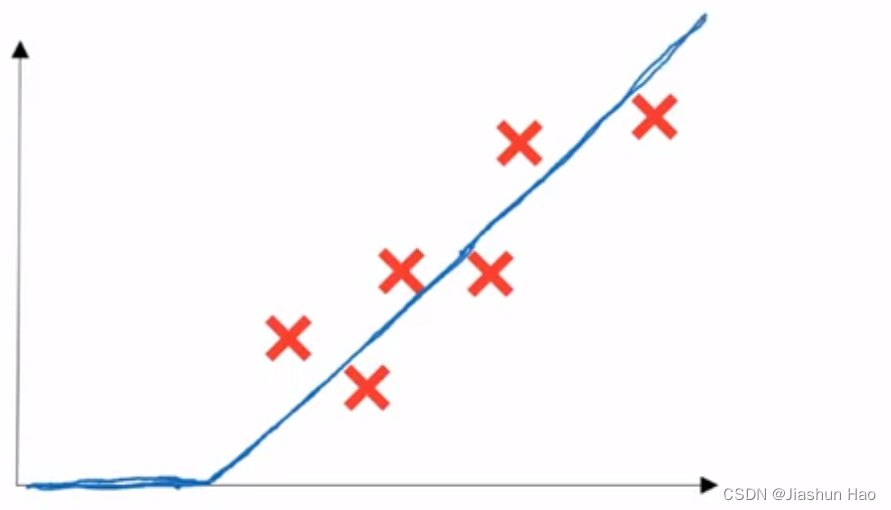
进一步,我们把这个 “房间大小和房价的关系函数” 抽象成一个小圆点,当输出房间大小X的时候,我们会得到一个对应的房价Y
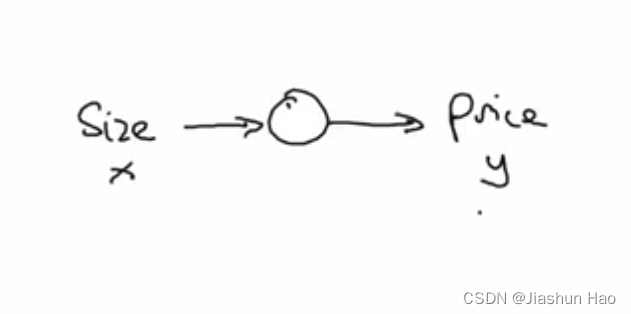
所以这个小圆点,就是神经网络中的一个 “神经元(Neurons)”
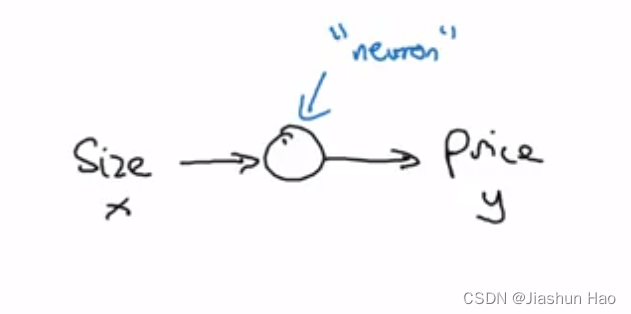
二、多个单神经元的神经网络
之前的输入数据,只有一个简单的"房子大小X". 即我们只需要考虑房子大小对于房价的影响。
那么,如果存在多个因素,比如房子的房间数、房子处于的地段位置、房子的使用寿命等…
这些考虑因素,输入数据中的 属性 或组成部分,在机器学习中叫 特征(Feature)。
假设,对于 每一个房子,现在我们要输入的特征有四个,分别是房子的大小(Size)、房间数量(Bedrooms)、房子的位置(Position)、周边富裕情况(Wealth)
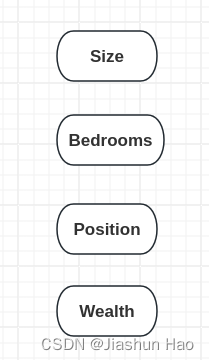
接下来,我们可以根据 每一个房子 的Size和Bedrooms,学习到一个函数(“小圆点/ 神经元”),来预测房子可以容纳人口的数量(Familys)
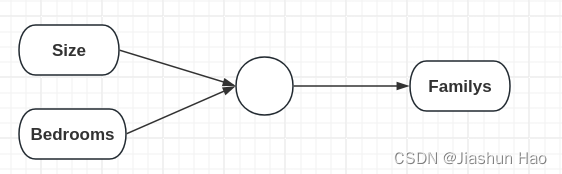
然后,我们可以根据 每一个房子 的Position,来预测房子的交通是否便利(Convenience)

然后,我们也可以根据 每一个房子 的Position和Wealth来预测附近的教学质量(School)
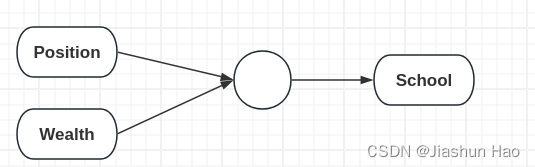
最后,我们可以通过 每一个房子 的人口的数量(Familys)、便利程度(Convenience)、教学质量(School)来学习到一个函数(“小圆点/ 神经元”),来预测 每一个房子 的价格。
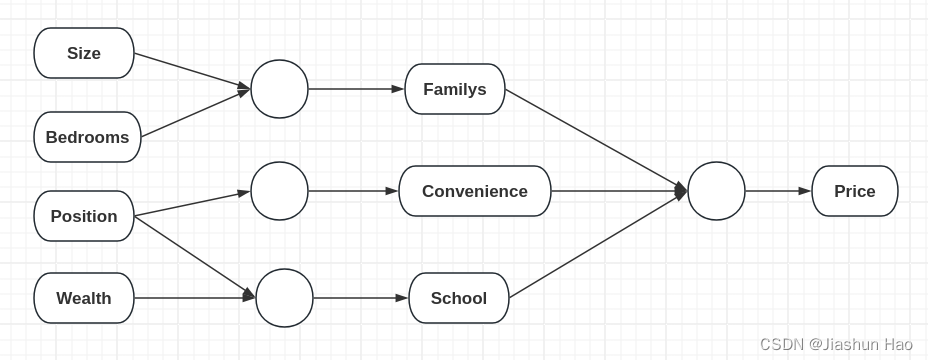
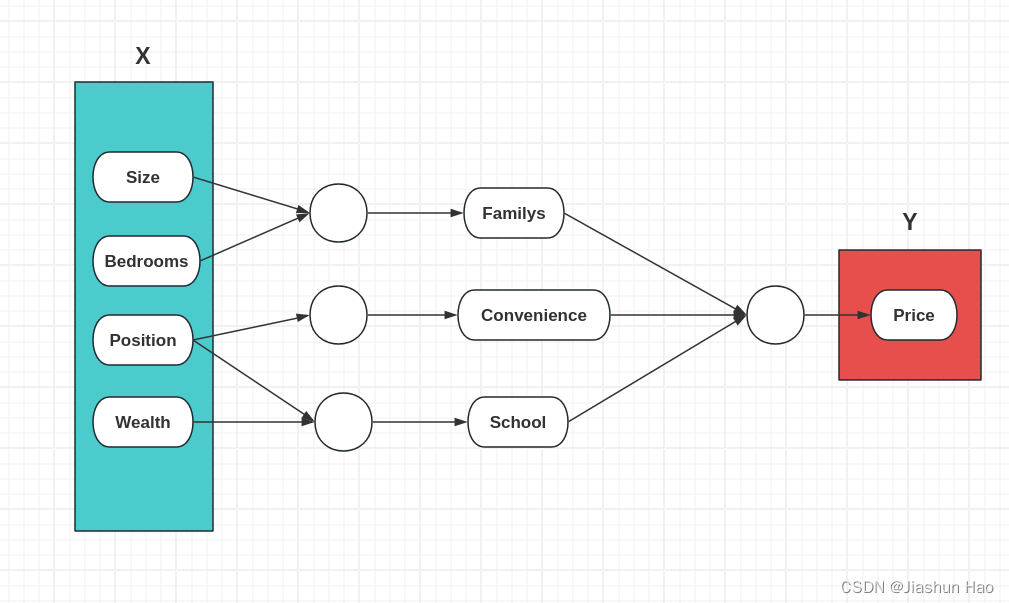
对于输入的,每一个房子 的四个原始特征,记作X。
对于最后得到的 每一个房子 的预测价格,记作Y
三、到底什么是机器学习?(重点)
1:什么是机器学习的训练?
1:我们需要搭建好神经网络的框架,设定好有多少层,每一层有多少神经元。
2:我们需要给每一个神经元设置一个固定的公式,和两个可变的参数(权重
W
W
W和偏差
b
b
b)
3:向这个框架给定 训练数据集中的每一个数据的多个特征X,然后也给定 每一个数据的希望预测结果Y
4:然后计算机就会根据“输入数据”和“理想结果”,自动学习 “怎么调节权重
W
W
W和偏差
b
b
b,可以使X变成Y?"
找权重 W W W和偏差 b b b的过程,就称为训练!
2:什么是模型?权重 W W W和偏差 b b b又是什么?
W W W:输入特征的权重
微观到每一个神经元来看,它们接受的输入的 训练数据集中的每一个数据的多个特征 N ≥ 1 N\geq1 N≥1,对于这多个特征,我们需要知道每一个输入特征在预测输出中的贡献大小。
哪些对于渴望的预测是是重要的,哪些是不重要的?
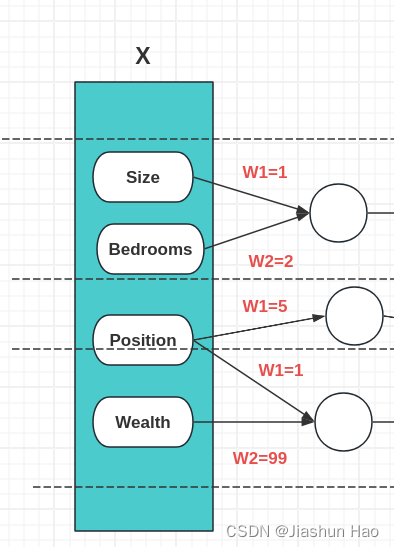
在每一个神经元中,我们给接收到的每一个特征一个自己的可变的权重,也就是 W W W
通过“学习”,模型可以自动增大对于渴望的预测有利的特征的权重,
通过“学习”,模型可以自动减小对于渴望的预测有利的特征的权重,
所以可以说,权重 W W W是作用于每一个神经元接收的多个输入的特征上。
b b b:每一个神经元的专属偏差
如果,无论怎么调整输入特征的权重,得到的计算公式还是不能把数据拟合成我们理想的输出该怎么办呢?
这个时候,我们可以引入偏差
b
b
b,来辅助权重
W
W
W调整神经元中的公式。
在每一个神经元中,权重
W
W
W的个数等于输入的特征的个数,即每一个特征都有一个自己的权重来微调。
而对于每一个神经元,有且只有一个单独的
b
b
b,用来直接调控当前神经元(当前的计算公式)。
此外,偏差的引入还有以下好处:
-
增加偏移能力
假设一个线性模型没有偏差项,即模型的表达式为 ( y = Wx ),其中 ( W ) 是权重,( x ) 是输入。这种模型限制了输出 ( y ) 必须通过原点,即当 ( x = 0 ) 时 ( y ) 也必须为 0。这种限制减少了模型的灵活性,因为现实世界的数据往往不是完全通过原点的。引入偏差 ( b )(即 ( y = Wx + b ))可以允许输出有一个基线偏移,无论输入 ( x ) 的值如何。 -
适应数据偏差
实际数据往往包含不同的偏差,如数据集整体可能偏向某个数值。没有偏差项的模型可能很难适应这种类型的数据结构,因为模型无法通过简单的权重调整来补偿这种偏向。偏差项可以帮助模型更好地适应数据的中心位置或其他统计特征。 -
提高非线性
在包含非线性激活函数的神经网络中,每个神经元的输出不仅取决于加权输入和偏差,还取决于激活函数如何处理这个加权和。偏差可以调整在激活函数中加权和的位置,从而影响激活函数的激活状态。这种调整是非常重要的,因为它可以帮助网络捕捉更复杂的模式和关系。 -
增加决策边界的灵活性
在分类问题中,决策边界是模型用来区分不同类别的界限。==如果没有偏差项,模型的决策边界可能只能是通过原点的直线或超平面,这大大限制了模型的有效性。==通过引入偏差,模型的决策边界可以是任意位置的直线或超平面,这大大提高了模型解决实际问题的能力。
3:神经元的里面是什么?
神经元里的基础函数:线性变换函数
在深度学习中,每一个神经单元(通常称为神经元或单元)的基础,都是执行一个线性变换函数。
即:
y
=
w
∗
x
+
b
y=w*x+b
y=w∗x+b
其中,
w
w
w 是权重,
b
b
b 是偏置,
x
x
x是输入数据或前一层的输出,
y
y
y是得到的预测结果。
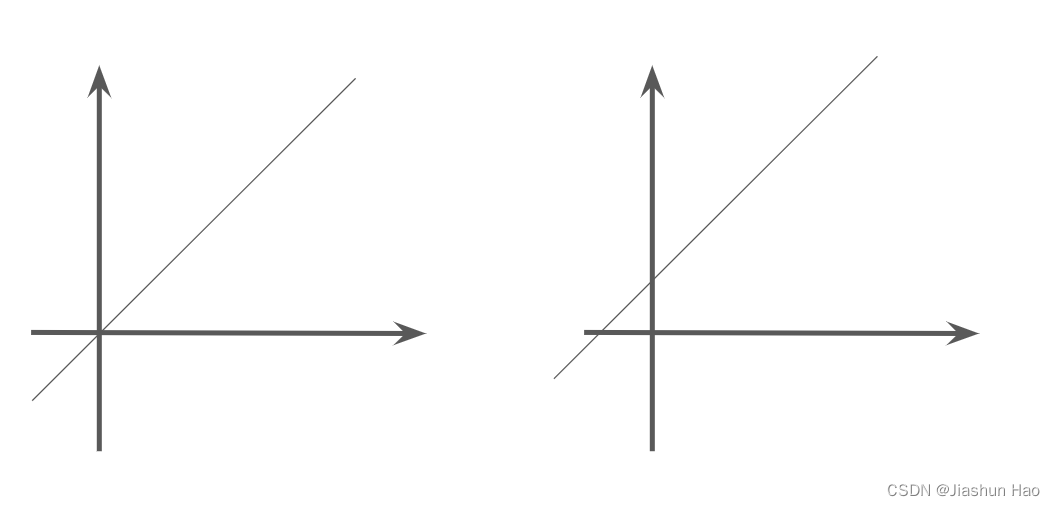
神经元里为了多样化任务的函数:激活函数
可以看到,线性变化的范围,
x
x
x和
y
y
y成正比,无限增长或无限缩小。
单单依靠这简单的线性变化,无法满足多样的需求。
因此,我们需要在这个线性变化函数的外面嵌套一个函数,这样的函数也成为激活函数(Activation Function)。
那什么又是嵌套呢?即,将线性变化函数的输出结果,作为激活函数的输入值。
举例:
对于逻辑回归任务,即预测一个事件发生的概率,有发生和不发生两种情况(二分类任务)
如果我们只是使用简单的线性变化函数,得到的得到的结果、输入
x
x
x和输出
y
y
y的关系可能是这样(假设不考虑
w
w
w和
b
b
b)

X有5种类型的输人,Y也有5种类型的输出,这样怎么判断事件发生的概率是发生了还是不发生呢?
聪明的小朋友也许想到了,我们可以以数字4为分界线,大于4的视为发生了,小于4的视为不发生。
在机器学习种,有一个思路和这样一模一样的函数专门应用于逻辑回归任务,即sigmoid函数。
对于它,只需要明白两点。
- 无论输入大小,它的输出范围:[0,1],它的图像是这样
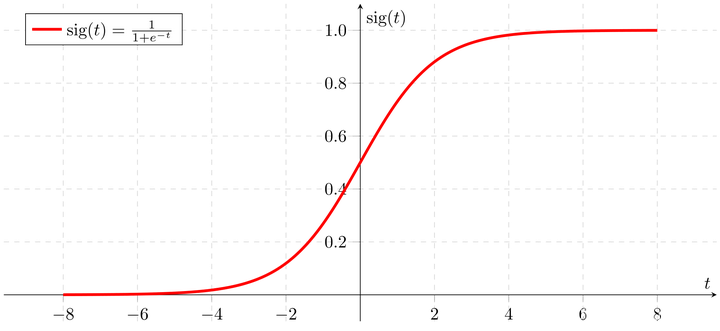
2. 公式如下:
y
=
1
1
+
e
−
x
y = \frac{1}{1 + e^{-x}}
y=1+e−x1
这个时候,我们就可以把得到的线性变化函数结果
y
y
y放到sigmoid函数里面— 或者直接将线性变化函数与sigmoid函数合并计算:
y = 1 1 + e − ( w ⋅ x + b ) y= \frac{1}{1 + e^{-( w \cdot x + b)}} y=1+e−(w⋅x+b)1
那么得到的输出结果可能就是这样:
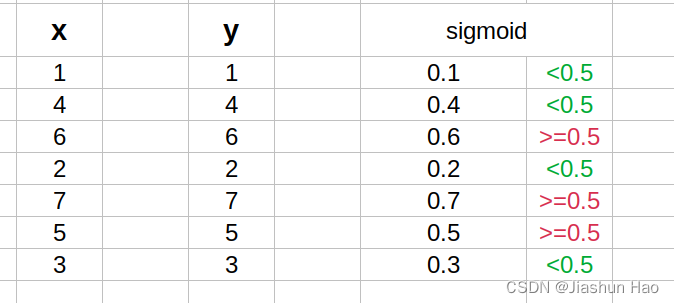
这里的sigmoid函数,即嵌套在线性函数外面用于多样化功能的函数,就叫激活函数.
四、损失函数和代价函数
1.标签和预测
在监督学习中,每一个输入的训练数据都有一个自己对应的标签(label),也就是我们希望数据对应的预测结果。
比如,我们想区分猫和狗
用 1 来标记“猫”,用 0 来标记“狗”,此时 1 就是数据“猫”的标签, 0 就是“狗”的标签。
标签 标签 标签在深度学习中有一个专门的符号,即 y y y。
当我们在模型使用/测试阶段的时候,我们会把“猫”和“狗”这俩个数据输入到模型中,让模型来捕获它们的信息给出预测, 那什么是预测呢?
预测 预测 预测,即是模型对于当前数据接近正类的概率,即是否为1的概率,在深度学习中也有一个专门的符号,即 y ^ \hat{y} y^。
比如模型的识别度很高的话,
也许模型识别“猫”的概率为0.9,即
y
^
\hat{y}
y^=0.9, 与“正类” 1 相近,归类为1。
也许模型识别“狗”的概率为0.1,即
y
^
\hat{y}
y^=0.1, 与“正类” 1 相远,归类为0。
2.损失函数
所谓损失呢,就是判断预测值 y ^ \hat{y} y^ 和标签 y y y 相差多少。
我们已经知道机器学习就是学习权重 w w w和偏差 b b b,而损失函数就是为调整权重 w w w和偏差 b b b提供指导。
损失函数的公式如下:
L o s s = L ( y , y ^ ) = − [ y log ( y ^ ) + ( 1 − y ) log ( 1 − y ^ ) ] Loss=L(y, \hat{y}) = -[y \log(\hat{y}) + (1 - y) \log(1 - \hat{y})] Loss=L(y,y^)=−[ylog(y^)+(1−y)log(1−y^)]
这个公式非常巧妙,如果测值 y ^ \hat{y} y^ 和标签 y y y相差大,那么损失值 L o s s Loss Loss 会特别大,反之会特别小。我们来验证一下。
前提补充:
l
o
g
2
(
1
)
=
0
log_2(1)=0
log2(1)=0
l
o
g
2
(
2
)
=
1
log_2(2)=1
log2(2)=1
二分类任务:
0
<
y
^
<
1
二分类任务:0 < \hat{y} < 1
二分类任务:0<y^<1
验证:假设
y
=
1
y=1
y=1
L
o
s
s
=
L
(
y
,
y
^
)
=
−
[
y
log
(
y
^
)
+
(
1
−
y
)
log
(
1
−
y
^
)
]
Loss=L(y, \hat{y}) = -[y \log(\hat{y}) + (1 - y) \log(1 - \hat{y})]
Loss=L(y,y^)=−[ylog(y^)+(1−y)log(1−y^)]
L
o
s
s
=
−
[
log
(
y
^
)
]
Loss = -[\log(\hat{y})]
Loss=−[log(y^)]
如果这个时候 y ^ \hat{y} y^ 的值为0.9, − log ( 0.9 ) ≈ 0.152 -\log(0.9)\approx0.152 −log(0.9)≈0.152 ,损失小。
如果这个时候 y ^ \hat{y} y^ 的值为0.1, − log ( 0.1 ) ≈ 3.322 -\log(0.1)\approx3.322 −log(0.1)≈3.322 ,损失大。
3.代价函数
上面的计算,我们都将输入的训练样本的个数视为1,所以只有一个标签 y y y 和一个预测 y ^ \hat{y} y^。
在训练中,我们时常有多个样本,数量计做为 i i i
所以每一个输入的样本的标签和预测为 y i y^i yi 和 y ^ i \hat{y}^i y^i
因为,损失的计算是作用于整个网络的,不是单个的神经元
因此,我们需要计算整体网络的损失,也就是代价计算。
总数据为 m m m 个 用 i i i 遍历每一个。
代价函数:
J = 1 m ∑ i = 1 m Loss ( y ( i ) , y ^ ( i ) ) J= \frac{1}{m} \sum_{i=1}^{m} \text{Loss}(y^{(i)}, \hat{y}^{(i)}) J=m1i=1∑mLoss(y(i),y^(i))
又因为,我们计算损失,是为了找到合适的
w
w
w 和
b
b
b, 使得损失变为最小。
所以公式的写法一般会将
w
w
w 和
b
b
b写入。
代价函数:
J ( w , b ) = 1 m ∑ i = 1 m L ( y ( i ) , y ^ ( i ) ) J(w, b) = \frac{1}{m} \sum_{i=1}^{m} \text{L}(y^{(i)}, \hat{y}^{(i)}) J(w,b)=m1i=1∑mL(y(i),y^(i))
代价的函数的图片如图:
即由 w w w 和 b b b 和代价 J J J 构成的三纬曲面
即存在一个
w
w
w 和
b
b
b 可以有一个最低的点
J
J
J
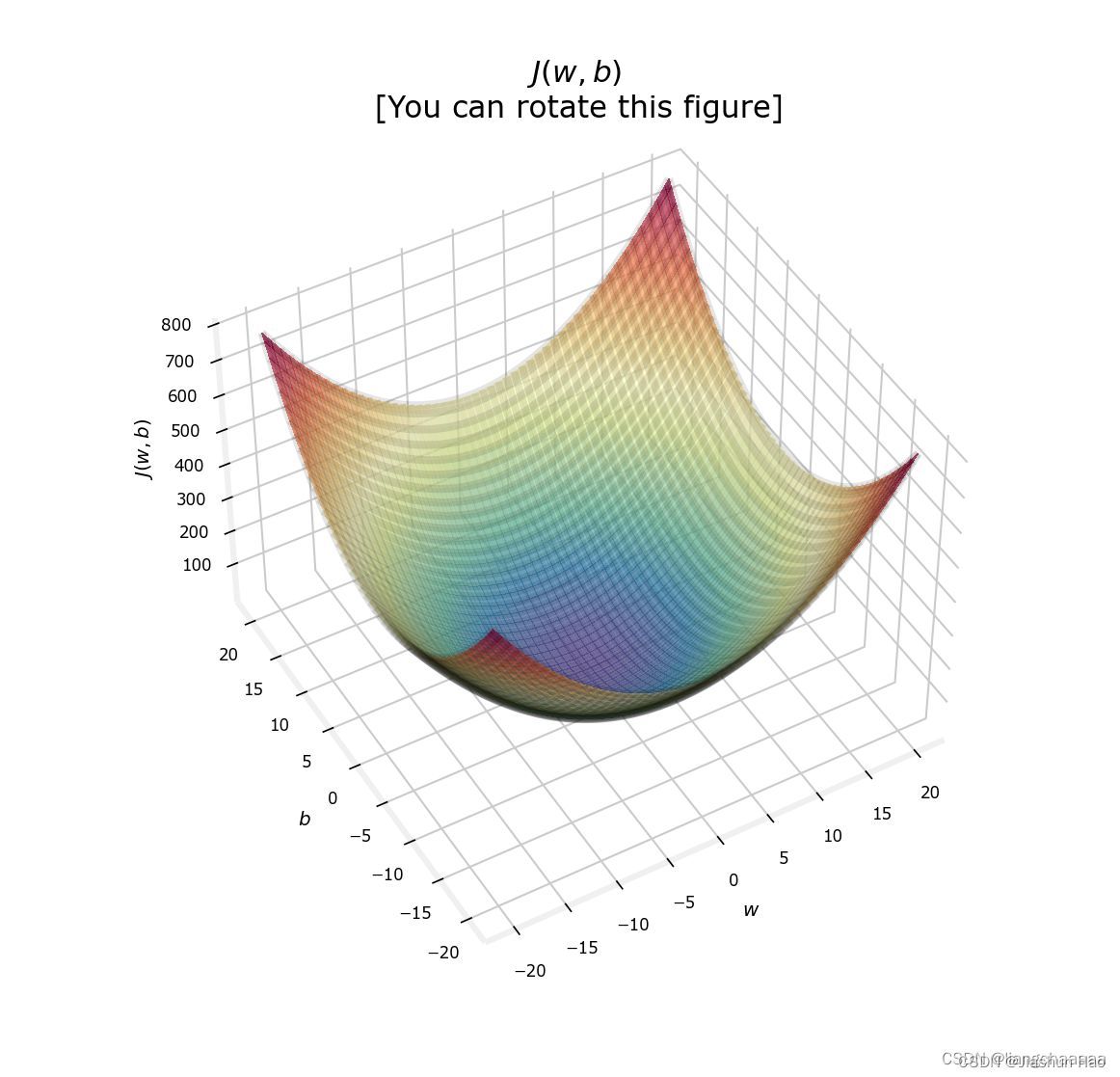
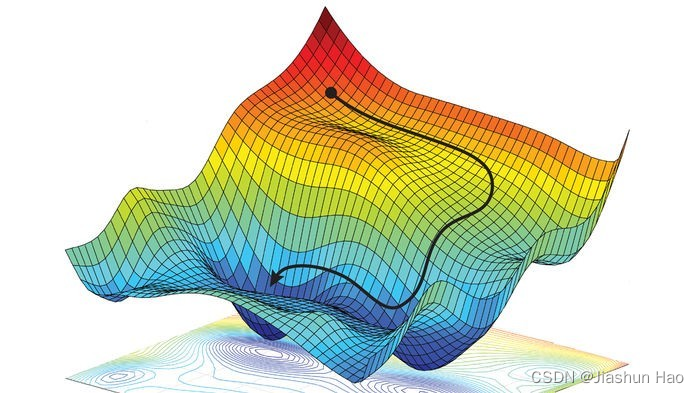
这个面通常是不规则的,上面为了说明找的特例。真实的情况可能是这样:
?、什么是深度学习?
深度学习的 “深度” 指的是神经网络中隐藏层的数量。
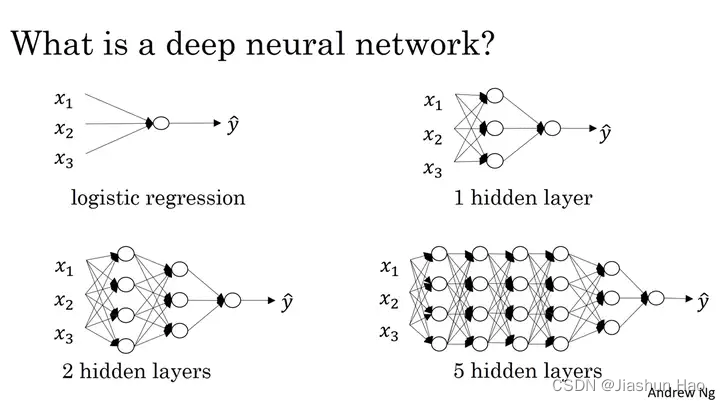
随着层数的增加,网络能够学习更复杂的特征,但同时也可能导致计算成本增加和模型训练难度加大。
神经网络通过一种叫做反向传播的学习算法来训练,它涉及到对网络输出的误差进行评估,并将误差反向传递回网络,以调整连接的权重,从而减少未来输出的误差。这个过程通常需要大量的数据和计算资源,这些我们下一篇再说。




![[开发|鸿蒙] DevEco Studio编译构建(笔记,持续更新)](https://img-blog.csdnimg.cn/direct/22d732e1f656413485c5f0918ef9b98e.png)