三重正交标架(Trihedron)
定义:三重正交标架是在三维空间中定义的一个坐标系,由三个互相垂直的向量构成。这些向量分别是:
切线向量(Tangent Vector) - 表示曲线在某一特定点处的切线方向。
主法线向量(Normal Vector) - 在曲线的每一点上垂直于切线向量,并且根据曲面的曲面法线(如果曲线位于某个曲面上)来定向。
副主法线向量(Binormal Vector) - 垂直于切线向量和主法线向量,完成三重正交标架的构建。
应用:三重正交标架在计算机图形学中用于:
-
定义沿曲线的局部坐标系,这对于曲面的参数化和建模非常重要。
-
分析曲线的曲率和扭率,因为曲率向量和扭率向量可以通过三重正交标架的导数来计算。
-
生成管道(Pipe)和扫掠(Sweeping)曲面,这些曲面沿着曲线拉伸一个截面。
三重正交标架法则(Trihedron Law)
定义:三重正交标架法则是一个在曲线的每一点上定义三重正交标架的规则。这个法则可以是显式的,也可以是隐式的,取决于它是基于特定的几何构造(如Frenet-Serret公式)还是基于更通用的几何约束。
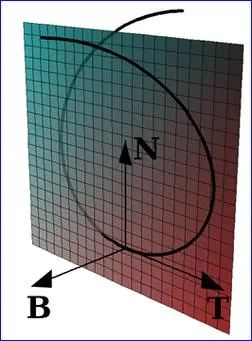
Frenet-Serret公式:在曲线r(t)的参数化形renet-Serret公式提供了一种计算三重正交标架的方法,其中 𝑡是曲线的参数。这些公式基于曲线的导数:

应用:三重正交标架法则在计算机辅助设计(CAD)和计算机辅助制造(CAM)中用于:
-
定义沿曲线的几何变化,这在创建复杂的3D几何形状时非常有用。
-
控制沿曲线的截面变形,以生成复杂的曲面,如螺旋曲面或螺旋管道。
-
实现高级曲面建模技术,如NURBS曲面的构建。
GeomFill_Frenet类继承自GeomFill_TrihedronLaw,用于在3D空间中定义沿曲线的Frenet三重正交标架法则。
GeomFill_Frenet类实现了Frenet三重正交标架法则,这在3D几何建模中用于定义沿曲线的局部坐标系,该坐标系由切线(Tangent)、主法线(Normal)和副主法线(BiNormal)构成。此类提供了计算三重正交标架及其导数的方法,并且能够处理曲线上的奇异点,这些奇异点是曲线的曲率或扭率不连续的点。
// 防止头文件被重复包含。
#ifndef _GeomFill_Frenet_HeaderFile
#define _GeomFill_Frenet_HeaderFile
#include <Standard.hxx> // 标准库的头文件
#include <TColStd_HArray1OfReal.hxx> // 用于存储实数数组的OCCT类
#include <GeomFill_TrihedronLaw.hxx> // 三重正交标架法则的基类
#include <Standard_Real.hxx> // 实数类型定义
#include <Standard_Integer.hxx> // 整型定义
#include <GeomAbs_Shape.hxx> // 几何形状定义
#include <TColStd_Array1OfReal.hxx> // 用于存储实数数组的OCCT类
#include <gp_Vec.hxx> // 几何向量类
// 声明GeomFill_Frenet类和它的句柄类型。
class GeomFill_Frenet;
DEFINE_STANDARD_HANDLE(GeomFill_Frenet, GeomFill_TrihedronLaw)
// 定义Frenet三重正交标架法则。
class GeomFill_Frenet : public GeomFill_TrihedronLaw
{
public: // 公共成员函数
// 构造函数
Standard_EXPORT GeomFill_Frenet();
// 复制构造函数,创建当前对象的一个副本
Standard_EXPORT virtual Handle(GeomFill_TrihedronLaw) Copy() const Standard_OVERRIDE;
// 初始化Frenet法则
Standard_EXPORT void Init();
// 设置Frenet法则的曲线
Standard_EXPORT virtual Standard_Boolean SetCurve(const Handle(Adaptor3d_Curve)& C) Standard_OVERRIDE;
// 计算曲线上参数为Param处的三重正交标架
Standard_EXPORT virtual Standard_Boolean D0(const Standard_Real Param, gp_Vec& Tangent, gp_Vec& Normal, gp_Vec& BiNormal) Standard_OVERRIDE;
// 计算曲线上参数为Param处的三重正交标架及其一阶导数
Standard_EXPORT virtual Standard_Boolean D1(const Standard_Real Param, gp_Vec& Tangent, gp_Vec& DTangent, gp_Vec& Normal, gp_Vec& DNormal, gp_Vec& BiNormal, gp_Vec& DBiNormal) Standard_OVERRIDE;
// 计算曲线上参数为Param处的三重正交标架及其一阶和二阶导数
Standard_EXPORT virtual Standard_Boolean D2(const Standard_Real Param, gp_Vec& Tangent, gp_Vec& DTangent, gp_Vec& D2Tangent, gp_Vec& Normal, gp_Vec& DNormal, gp_Vec& D2Normal, gp_Vec& BiNormal, gp_Vec& DBiNormal, gp_Vec& D2BiNormal) Standard_OVERRIDE;
// 返回连续性S的区间数量
Standard_EXPORT virtual Standard_Integer NbIntervals(const GeomAbs_Shape S) const Standard_OVERRIDE;
// 存储连续性S的区间的边界参数
Standard_EXPORT virtual void Intervals(TColStd_Array1OfReal& T, const GeomAbs_Shape S) const Standard_OVERRIDE;
// 获取Tangent(t)和Normal(t)的平均值,这对于快速近似有理曲面非常有用
Standard_EXPORT virtual void GetAverageLaw(gp_Vec& ATangent, gp_Vec& ANormal, gp_Vec& ABiNormal) Standard_OVERRIDE;
// 检查法则是否恒定
Standard_EXPORT virtual Standard_Boolean IsConstant() const Standard_OVERRIDE;
// 返回True,表示法则仅由3D曲线确定
Standard_EXPORT virtual Standard_Boolean IsOnlyBy3dCurve() const Standard_OVERRIDE;
// 实现运行时类型识别(RTTI)
DEFINE_STANDARD_RTTIEXT(GeomFill_Frenet, GeomFill_TrihedronLaw)
protected: // 保护成员函数
private: // 私有成员函数和变量
// 检查U是否为奇异点,并返回奇异点的索引
Standard_EXPORT Standard_Boolean IsSingular(const Standard_Real U, Standard_Integer& Index) const;
// 处理奇异点
Standard_EXPORT Standard_Boolean DoSingular(const Standard_Real U, const Standard_Integer Index, gp_Vec& Tangent, gp_Vec& BiNormal, Standard_Integer& n, Standard_Integer& k, Standard_Integer& TFlag, Standard_Integer& BNFlag, Standard_Real& Delta);
// 计算奇异点处的三重正交标架
Standard_EXPORT Standard_Boolean SingularD0(const Standard_Real Param, const Standard_Integer Index, gp_Vec& Tangent, gp_Vec& Normal, gp_Vec& BiNormal, Standard_Real& Delta);
// 计算奇异点处的三重正交标架及其一阶导数
Standard_EXPORT Standard_Boolean SingularD1(const Standard_Real Param, const Standard_Integer Index, gp_Vec& Tangent, gp_Vec& DTangent, gp_Vec& Normal, gp_Vec& DNormal, gp_Vec& BiNormal, gp_Vec& DBiNormal, Standard_Real& Delta);
// 计算奇异点处的三重正交标架及其一阶和二阶导数
Standard_EXPORT Standard_Boolean SingularD2(const Standard_Real Param, const Standard_Integer Index, gp_Vec& Tangent, gp_Vec& DTangent, gp_Vec& D2Tangent, gp_Vec& Normal, gp_Vec& DNormal, gp_Vec& D2Normal, gp_Vec& BiNormal, gp_Vec& DBiNormal, gp_Vec& D2BiNormal, Standard_Real& Delta);
// 旋转三重正交标架以使给定的“Tangent”和“NewTangent”轴重合
Standard_EXPORT Standard_Boolean RotateTrihedron(gp_Vec& Tangent, gp_Vec& Normal, gp_Vec& BiNormal, const gp_Vec& NewTangent) const;
// 存储曲线上的点、奇异点数组和奇异点长度数组的句柄
gp_Pnt P;
Handle(TColStd_HArray1OfReal) mySngl;
Handle(TColStd_HArray1OfReal) mySnglLen;
Standard_Boolean isSngl;
};
#endif // _GeomFill_Frenet_HeaderFile