DS二叉搜索树

news2024/9/22 7:41:33

前言

我们在数据结构初阶专栏已经对二叉树进行了介绍并用C语言做了实现，但是当时没有对二叉搜树进行介绍，而是把他放到数据结构进阶构专栏的第一期来介绍，原因是后面的map和set（红黑树）是基于搜索树的，这里介绍完后再去学习他们的成本会低一点！

本期内容介绍

二叉搜索树介绍

二叉搜索树的实现

二叉搜索树的应用

二叉搜索树的性能分析

二叉搜索树的介绍

什么是二叉搜索树？

二叉搜索树又称二叉排序树（走中序就是有序的）或二叉查找树。他是一颗空树或满足以下性质的二叉树！

1、如果它的左子树不为空，则左子树的所有节点的值都小于根节点的值

2、如果它的右子树不为空，则右子树的所有节点的值都大于根节点的值

3、它的左右子树也必须都为二叉搜索树

一般把二叉搜索树的节点的值叫做键值（key），一个键值唯一标识唯一一个节点！所以一般的key模型的二叉搜索树是不允许修改的（key_value模型仅可以修改value）；因为在key模型的二叉搜索树中修改了key值会影响二叉搜索的搜索性，修改后可能就不在符合左边比根节点小，右边比根节点大的性质了！！！

二叉搜索树的实现

由于二叉搜索树是不允许修改键值(key)的，他主要作用是查询，所以没有修改接口。

OK，还是和以前一样，先搭个架子出来：我们得有节点的类专门搞节点，然后一个二叉搜索树的类专门负责查找等操作！

template<class K>
struct BSTreeNode
{
	BSTreeNode* _left;
	BSTreeNode* _right;
	K _key;

	BSTreeNode(const K& key)
		:_left(nullptr)
		, _right(nullptr)
		, _key(key)
	{}
};

template<class K>
class BSTree
{
	typedef BSTreeNode<K> Node;
public:

private:
	Node* _root = nullptr;//只有一个成员，给一个缺省参数可以不用自己写构造了
};

下面就是实现插入、查询和删除的接口操作了！

insert

实现思路：

如果是第一次插入即根节点为空则直接new一个值为key的节点连接到_root返回即可！

如果不是第一次插入，则从父节点开始查找合适的插入位置并用parent的变量记录合适位置的父节点的值，如果比当前的节点大，去右边，否则去左边，直到为空即找到了合适的位置，插入！如果是等于说明要插入的值引进存在直接返回！

最后找到了插入位置new一个键值为key的节点连接到合适位置的父节点即可！

但是这里要插到做还是右呢？如果key的值比parent的值大插入到右边，否则插入到左边！

bool insert(const K& key)
{
	if (_root == nullptr)//第一次插入
	{
		_root = new Node(key);
		return true;
	}

	Node* parent = nullptr;//记录要插入节点的父节点的位置
	Node* cur = _root;
	while (cur)
	{
		if (cur->_key > key)//要插入的值比当前节点的值小
		{
			parent = cur;
			cur = cur->_left;//去当前节点的左边
		}
		else if (cur->_key < key)//要插入的值比当前节点的值大
		{
			parent = cur;
			cur = cur->_right;//去当前节点的右边
		}
		else
		{
			return false;//要插入的值已经存在
		}
	}

	//找到了要插入节点的合适位置
	cur = new Node(key);//申请一个键值为key的节点
	if (parent->_key < key)//key的值比父节点小
	{
		parent->_right = cur;//连接到父节点的右边
	}
	else
	{
		parent->_left = cur;//否则连接到父节点的左边
	}

	return true;//插入成功
}

OK，我们知道他的中序是有序的，所以我们可以插入一些乱序的数字然后走个中序看看是否是有序的即可验证师插入！

InOrder

实现思路：先遍历左子树 --> 根 -->右子树

但是这的根节点是BSTree私有的，咋办呢？解决方案右以下几种：

1、把你的测试函数搞成友元，就可以在测试函数中访问_root了（强烈不推荐）

2、提供get和set函数

3、把中序搞成私有的子函数，在提供一个共有的把子函数套一层（推荐）

void _Inorder(const Node* _root)
{
	if (_root == nullptr)
	{
		return;
	}

	_Inorder(_root->_left);
	cout << _root->_key << " ";
	_Inorder(_root->_right);
}

OK，验证一下：

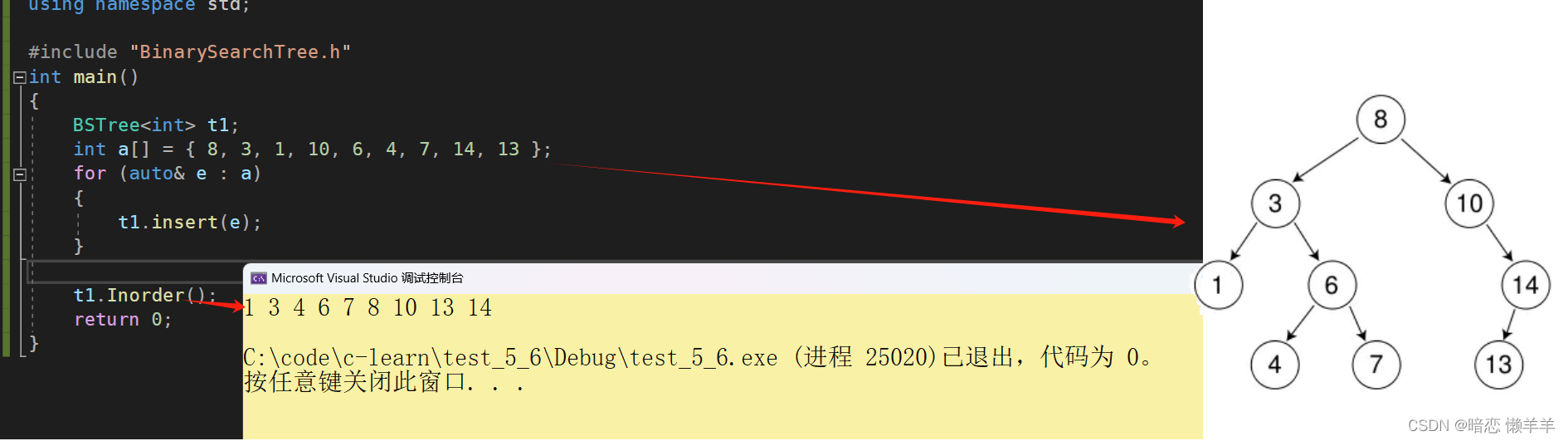
Find

实现思路：比较当前节点的值和key的值，如果比key大去右边，否则去左边找！

bool Find(const K& key)
{
	Node* cur = _root;
	while (cur)
	{
		if (cur->_key > key)
		{
			cur = cur->_left;
		}
		else if(cur->_key < key)
		{
			cur = cur->_right;
		}
		else
		{
			return true;//找到了
		}
	}

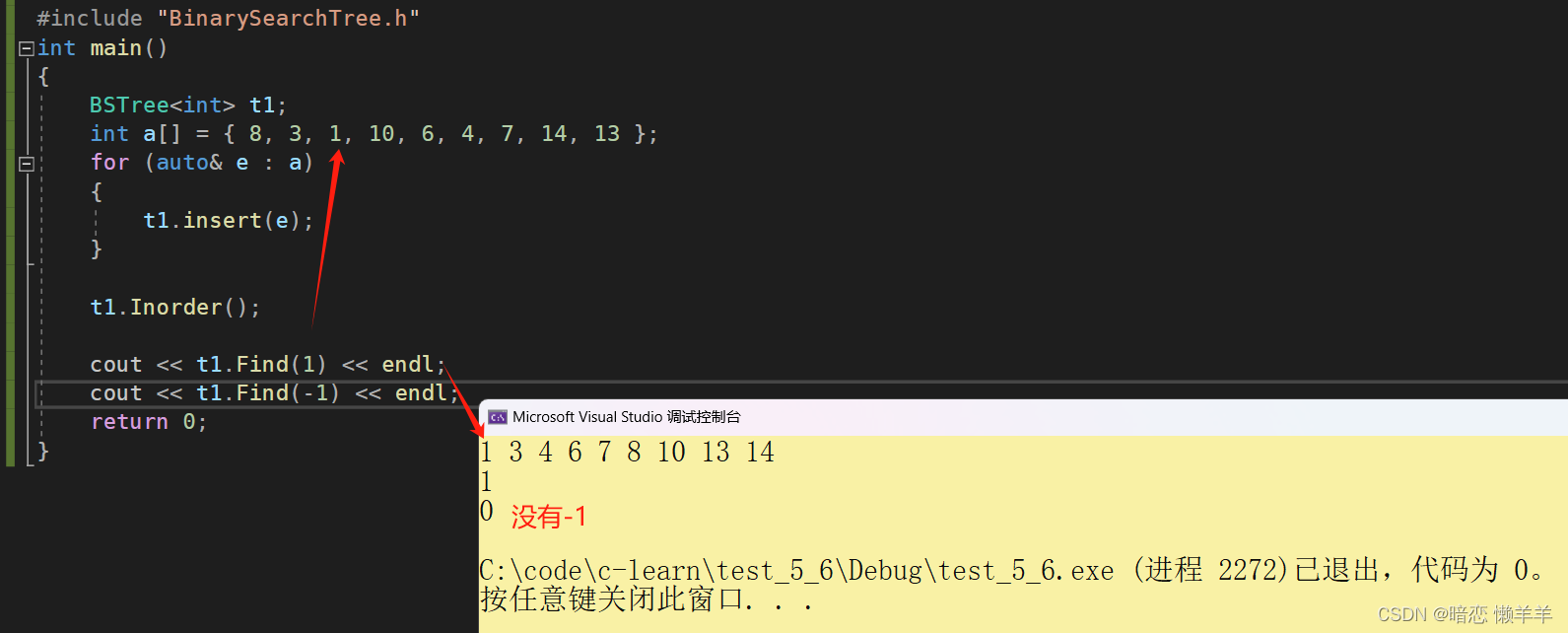
	return false;//没找到
}

Erase

实现思路

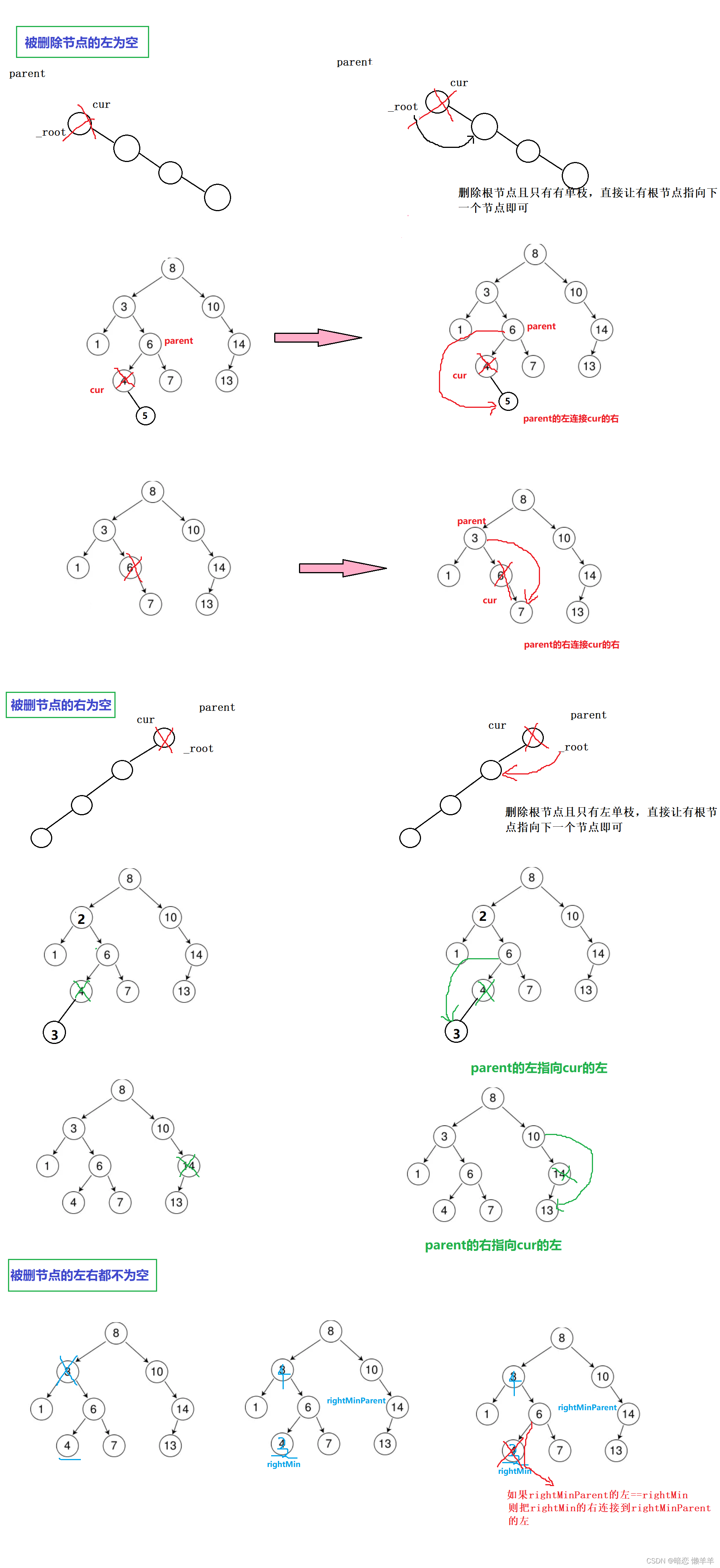
删除可以分为4种情况：1、被删节点的左为空   2、被删节点的右为空  3、被删节点的左右都为空  4、被删节点的左右都不为空。前三中只需要特殊处理一下可以合并为两种！注意：所有的删除都得找到这个节点，否则直接返回false;

被删节点的左为空

        1、如果当前节点是根节点且只有右单枝，让根节点指向它的右单枝的下一个

        2、不是根节点，如果被删节点==它的父节点的左，则把他的右连接到父亲的左

              如果被删节点==它的父节点的右，则把他的右连接到父亲的右

被删节点的右为空 

        1、如果当前节点是根节点且只有左单枝，让根节点指向它的左单枝的下一个

        2、不是根节点，如果被删节点==它的父节点的左，则把他的左连接到父亲的左

              如果被删节点==它的父节点的右，则把他的左连接到父亲的右

被删节点的左右都不为空

        用替换法删除即找一个合适的节点替他删除！可以找左子树最大（右）或 右子树最左         （小）的节点来替换。

        找到替换的节点后可以交换键值也可以赋值，然后删除替换节点即可！

bool Erase(const K& key)
{
	Node* parent = nullptr;
	Node* cur = _root;
	while (cur)
	{
		if (cur->_key > key)//比key大，往左找
		{
			parent = cur;
			cur = cur->_left;
		}
		else if (cur->_key < key)//比key小，往右找
		{
			parent = cur;
			cur = cur->_right;
		}
		else//找到了
		{
			if (cur->_left == nullptr)//被删除节点的左为空
			{
				if (_root == cur)//删除根且只有右枝没有左枝
				{
					_root = cur->_right;//让根指向它的右
				}
				else
				{
					if (parent->_left == cur)//父亲的左==cur，把cur的右连接到父亲的左
					{
						parent->_left = cur->_right;
					}
					else//父亲的右==cur，把cur的右连接到父亲的右
					{
						parent->_right = cur->_right;
					}
				}

				delete cur;
			}
			else if (cur->_right == nullptr)//被删除节点的右为空
			{
				if (_root == cur)//删除根且只有左枝没有右枝
				{
					_root = cur->_left;//让根指向它的左
				}
				else
				{
					if (parent->_left == cur)//父亲的左==cur，把cur的左连接到父亲的左
					{
						parent->_left = cur->_left;
					}
					else
					{
						parent->_right = cur->_left;//父亲的右==cur，把cur的右连接到父亲的左
					}
				}

				delete cur;
			}
			else//被删除节点的左右都不为空则用替换法删除即找到一个合适的节点来替他被删（左子树最（大）右，或右子树的最（小）左）
			{
				Node* rightMinParent = cur;//右子树最（小）左节点的父亲
				Node* rightMin = cur->_right;//右子树的最左节点
				while (rightMin->_left)
				{
					rightMinParent = rightMin;
					rightMin = rightMin->_left;
				}

				swap(cur->_key, rightMin->_key);//右子树左节点与被删节点的值交换
					
				if (rightMinParent->_left == rightMin)//如果rightMinParent的左==rightMin
				{
					rightMinParent->_left = rightMin->_right;//则把rightMin的右连接到rightMinParent的左
				}
				else//如果rightMinParent的右==rightMin
				{
					rightMinParent->_right = rightMin->_right;//则把rightMin的右连接到rightMinParent的右
				}

				delete rightMin;
			}

			return true;
		}
	}

	return false;
}

OK，验证一下：

析构函数

因为只有一个成员，所以直接给一个缺省值就不用写构造了！析构得写，和二叉树的销毁一样！先左子树销毁-->右子树销毁-->根销毁，可以和中序一样搞一个子函数外面套一下即可！

void Destory(Node*& root)
{
	if (root == nullptr)
		return;

	Destory(root->_left);
	Destory(root->_right);

	delete root;
	root = nullptr;
}
~BSTree()
{
	Destory(_root);
}

key模型的全部源码

#pragma once

template<class K>
struct BSTreeNode
{
	BSTreeNode* _left;
	BSTreeNode* _right;
	K _key;

	BSTreeNode(const K& key)
		:_left(nullptr)
		,_right(nullptr)
		,_key(key)
	{}
};

template<class K>
class BSTree
{
	typedef BSTreeNode<K> Node;
public:
	bool insert(const K& key)
	{
		if (_root == nullptr)//第一次插入
		{
			_root = new Node(key);
			return true;
		}

		Node* parent = nullptr;//记录要插入节点的父节点的位置
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key > key)//要插入的值比当前节点的值小
			{
				parent = cur;
				cur = cur->_left;//去当前节点的左边
			}
			else if (cur->_key < key)//要插入的值比当前节点的值大
			{
				parent = cur;
				cur = cur->_right;//去当前节点的右边
			}
			else
			{
				return false;//要插入的值已经存在
			}
		}

		//找到了要插入节点的合适位置
		cur = new Node(key);//申请一个键值为key的节点
		if (parent->_key < key)//key的值比父节点小
		{
			parent->_right = cur;//连接到父节点的右边
		}
		else
		{
			parent->_left = cur;//否则连接到父节点的左边
		}

		return true;//插入成功
	}

	bool Find(const K& key)
	{
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key > key)
			{
				cur = cur->_left;
			}
			else if(cur->_key < key)
			{
				cur = cur->_right;
			}
			else
			{
				return true;//找到了
			}
		}

		return false;//没找到
	}

bool Erase(const K& key)
{
	Node* parent = nullptr;
	Node* cur = _root;
	while (cur)
	{
		if (cur->_key > key)//比key大，往左找
		{
			parent = cur;
			cur = cur->_left;
		}
		else if (cur->_key < key)//比key小，往右找
		{
			parent = cur;
			cur = cur->_right;
		}
		else//找到了
		{
			if (cur->_left == nullptr)//被删除节点的左为空
			{
				if (_root == cur)//删除根且只有右枝没有左枝
				{
					_root = cur->_right;//让根指向它的右
				}
				else
				{
					if (parent->_left == cur)//父亲的左==cur，把cur的右连接到父亲的左
					{
						parent->_left = cur->_right;
					}
					else//父亲的右==cur，把cur的右连接到父亲的右
					{
						parent->_right = cur->_right;
					}
				}

				delete cur;
			}
			else if (cur->_right == nullptr)//被删除节点的右为空
			{
				if (_root == cur)//删除根且只有左枝没有右枝
				{
					_root = cur->_left;//让根指向它的左
				}
				else
				{
					if (parent->_left == cur)//父亲的左==cur，把cur的左连接到父亲的左
					{
						parent->_left = cur->_left;
					}
					else
					{
						parent->_right = cur->_left;//父亲的右==cur，把cur的右连接到父亲的左
					}
				}

				delete cur;
			}
			else//被删除节点的左右都不为空则用替换法删除即找到一个合适的节点来替他被删（左子树最（大）右，或右子树的最（小）左）
			{
				Node* rightMinParent = cur;//右子树最（小）左节点的父亲
				Node* rightMin = cur->_right;//右子树的最左节点
				while (rightMin->_left)
				{
					rightMinParent = rightMin;
					rightMin = rightMin->_left;
				}

				swap(cur->_key, rightMin->_key);//右子树左节点与被删节点的值交换
					
				if (rightMinParent->_left == rightMin)//如果rightMinParent的左==rightMin
				{
					rightMinParent->_left = rightMin->_right;//则把rightMin的右连接到rightMinParent的左
				}
				else//如果rightMinParent的右==rightMin
				{
					rightMinParent->_right = rightMin->_right;//则把rightMin的右连接到rightMinParent的右
				}

				delete rightMin;
			}

			return true;
		}
	}

	return false;
}

	void Inorder()
	{
		_Inorder(_root);
		cout << endl;
	}

	~BSTree()
	{
		Destory(_root);
	}

private:
	void _Inorder(const Node* _root)
	{
		if (_root == nullptr)
		{
			return;
		}

		_Inorder(_root->_left);
		cout << _root->_key << " ";
		_Inorder(_root->_right);
	}

	void Destory(Node*& root)
	{
		if (root == nullptr)
			return;

		Destory(root->_left);
		Destory(root->_right);

		delete root;
		root = nullptr;
	}

private:
	Node* _root = nullptr;//只有一个成员，给一个缺省参数可以不用自己写构造了
};

二叉搜索树的应用

1、K模型：就是我们上面介绍和实现的key模型，K模型中只存键值key，不可被修改！这个在生活中也是很常见的，比如说20万个单词找出拼写错误的单词！此时你只需要根据单词库中的单词建立一个key模型的搜索树即可，然后一一查找即可，如果是false的就是错误的！另外，宿舍的门禁系统，你刷脸或刷卡时会放你进去，这个也是一个key模型的搜索树！

2、KV模型：每个节点中不仅存一个键值key还要存一个key对应的value。即<KV>键值对。这个也是很常见的，比如说英汉词典，你的学号对应你等！

key_value模型全部源代码

上面K模型已经实现了，这里KV模型在上面的K上稍加修改即可（插入的时候多加一个value）！

namespace key_value
{
	template<class K, class V>
	struct BSTreeNode
	{
		BSTreeNode* _left;
		BSTreeNode* _right;
		K _key;
		V _value;

		BSTreeNode(const K& key, const V& value)
			:_left(nullptr)
			, _right(nullptr)
			, _key(key)
			,_value(value)
		{}
	};

	template<class K, class V>
	class BSTree
	{
		typedef BSTreeNode<K, V> Node;
	public:
		bool insert(const K& key, const V& value)
		{
			if (_root == nullptr)//第一次插入
			{
				_root = new Node(key, value);
				return true;
			}

			Node* parent = nullptr;//记录要插入节点的父节点的位置
			Node* cur = _root;
			while (cur)
			{
				if (cur->_key > key)//要插入的值比当前节点的值小
				{
					parent = cur;
					cur = cur->_left;//去当前节点的左边
				}
				else if (cur->_key < key)//要插入的值比当前节点的值大
				{
					parent = cur;
					cur = cur->_right;//去当前节点的右边
				}
				else
				{
					return false;//要插入的值已经存在
				}
			}

			//找到了要插入节点的合适位置
			cur = new Node(key, value);//申请一个键值为key的节点
			if (parent->_key < key)//key的值比父节点小
			{
				parent->_right = cur;//连接到父节点的右边
			}
			else
			{
				parent->_left = cur;//否则连接到父节点的左边
			}

			return true;//插入成功
		}

		Node* Find(const K& key)
		{
			Node* cur = _root;
			while (cur)
			{
				if (cur->_key > key)
				{
					cur = cur->_left;
				}
				else if (cur->_key < key)
				{
					cur = cur->_right;
				}
				else
				{
					return cur;//找到了
				}
			}

			return cur;//没找到
		}

		bool Erase(const K& key)
		{
			Node* parent = nullptr;
			Node* cur = _root;
			while (cur)
			{
				if (cur->_key > key)//比key大，往左找
				{
					parent = cur;
					cur = cur->_left;
				}
				else if (cur->_key < key)//比key小，往右找
				{
					parent = cur;
					cur = cur->_right;
				}
				else//找到了
				{
					if (cur->_left == nullptr)//被删除节点的左为空
					{
						if (_root == cur)//删除根且只有右枝没有左枝
						{
							_root = cur->_right;//让根指向它的右
						}
						else
						{
							if (parent->_left == cur)//父亲的左==cur，把cur的右连接到父亲的左
							{
								parent->_left = cur->_right;
							}
							else//父亲的右==cur，把cur的右连接到父亲的右
							{
								parent->_right = cur->_right;
							}
						}

						delete cur;
					}
					else if (cur->_right == nullptr)//被删除节点的右为空
					{
						if (_root == cur)//删除根且只有左枝没有右枝
						{
							_root = cur->_left;//让根指向它的左
						}
						else
						{
							if (parent->_left == cur)//父亲的左==cur，把cur的左连接到父亲的左
							{
								parent->_left = cur->_left;
							}
							else
							{
								parent->_right = cur->_left;//父亲的右==cur，把cur的右连接到父亲的左
							}
						}

						delete cur;
					}
					else//被删除节点的左右都不为空则用替换法删除即找到一个合适的节点来替他被删（左子树最（大）右，或右子树的最（小）左）
					{
						Node* rightMinParent = cur;//右子树最（小）左节点的父亲
						Node* rightMin = cur->_right;//右子树的最左节点
						while (rightMin->_left)
						{
							rightMinParent = rightMin;
							rightMin = rightMin->_left;
						}

						swap(cur->_key, rightMin->_key);//右子树左节点与被删节点的值交换

						if (rightMinParent->_left == rightMin)//如果rightMinParent的左==rightMin
						{
							rightMinParent->_left = rightMin->_right;//则把rightMin的右连接到rightMinParent的左
						}
						else//如果rightMinParent的右==rightMin
						{
							rightMinParent->_right = rightMin->_right;//则把rightMin的右连接到rightMinParent的右
						}

						delete rightMin;
					}

					return true;
				}
			}

			return false;
		}

		void Inorder()
		{
			_Inorder(_root);
			cout << endl;
		}

		~BSTree()
		{
			Destory(_root);
		}

	private:
		void _Inorder(const Node* _root)
		{
			if (_root == nullptr)
			{
				return;
			}

			_Inorder(_root->_left);
			cout << _root->_key << " -> " << _root->_value << endl;
			_Inorder(_root->_right);
		}

		void Destory(Node*& root)
		{
			if (root == nullptr)
				return;

			Destory(root->_left);
			Destory(root->_right);

			delete root;
			root = nullptr;
		}

	private:
		Node* _root = nullptr;//只有一个成员，给一个缺省参数可以不用自己写构造了
	};
}

可以一个类似于英汉单词的效果：

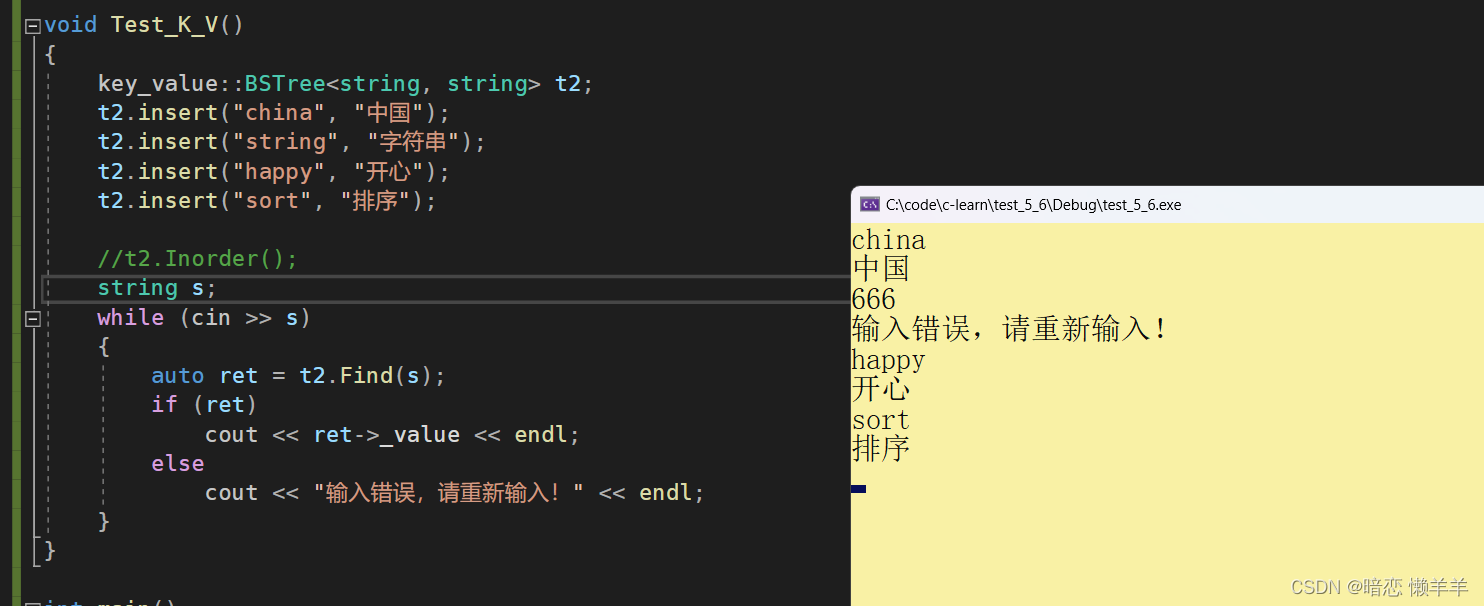
当然还可以统计某些东西的次数等！这里就不演示了！

二叉搜索树的性能分析

要执行插入和删除的操作的前提是得查找到相关的位置或元素，所以查找的效率代表了插入和删除的性能！我们来分析一下二叉搜索树的查找的时间复杂度：如果正常情况下是最多查找高度次所以时间复杂度是:O(logN)但是如果这个数是类似于链表的情况的话就是O（N）了！

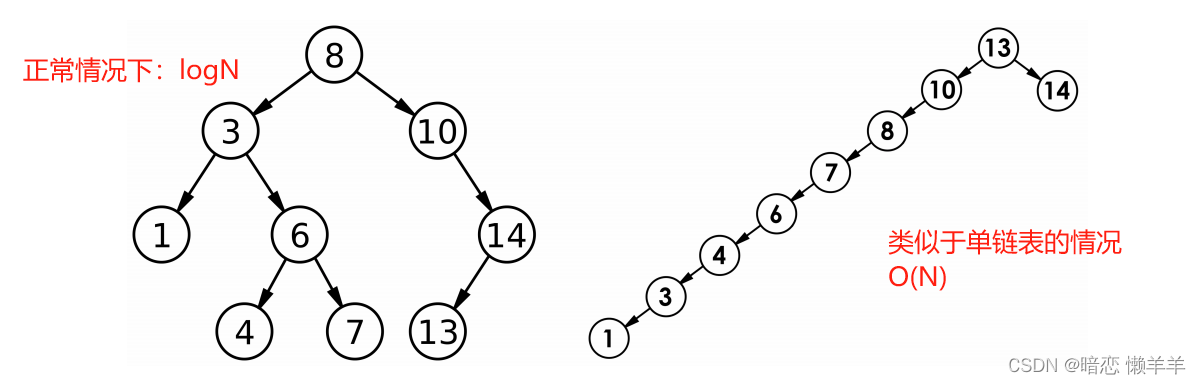
这里你可能会担心，如果极端情况下真的退化成单链表那二叉搜索树的搜索性能就消失了，那该咋办呢？其实这个问题已经得到了解决！就是我们后面要介绍的AVL树和红黑树！马上后面会介绍的！

OK，好兄弟，本期分享就到这里，我们下期再见！

结束语：山高路远，看世界，也找自己。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1645723.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

LIUNX系统编程：进程池的实现

LIUNX系统编程：进程池的实现

1.什么是进程池 每一个可执行程序&#xff0c;在被执行前都要转化为进程&#xff0c;操作系统都要为其创建PCB&#xff0c;地址空间&#xff0c;页表&#xff0c;构建映射关系&#xff0c;进程池就是创建进程时&#xff0c;创建很多个进程&#xff0c;如果要执行程序&#xff…
阅读更多...
ROS仿真小车与SLAM

ROS仿真小车与SLAM

ROS仿真小车与SLAM ROS中机器小车的仿真实验一、建立模型1.创建功能包导入依赖&#xff1a;创建urdf,launch文件&#xff1a; 2.可视化 二、添加雷达传感器1.编写xacro文件2.集成launch文件3.添加摄像头和雷达传感器my_camera.urdf.xacro文件&#xff1a;my_laser.urdf.xacro文…
阅读更多...
Retrofit源码解析

Retrofit源码解析

整体概述 这个是我看完Retrofit的源码后&#xff0c;站在一个高的维度俯瞰整个Retrofit的架构得到的结论。 Retrofit的出现就是对OKHttp做了一个二次封装&#xff0c;为什么要封装&#xff1f;我认为核心目的就是让使用更加的方便。都对哪里进行了封装&#xff1f; 封装了请求…
阅读更多...
从一到无穷大 #25 DataFusion：可嵌入，可扩展的模块化工业级计算引擎实现

从一到无穷大 #25 DataFusion：可嵌入，可扩展的模块化工业级计算引擎实现

本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 本作品 (李兆龙 博文, 由 李兆龙 创作)&#xff0c;由 李兆龙 确认&#xff0c;转载请注明版权。 文章目录 引言架构总览与可扩展性Catalog and Data SourcesFront End逻辑计划与逻辑计划优化器…
阅读更多...
c3 笔记6 认识css样式表

c3 笔记6 认识css样式表

<link>与import应该如何选择?事实上&#xff0c;使用link与import链接外部样式文件的效果看起来是一样的&#xff0c;区别在于<link>是HTML标记而import属于CSS语法。<link>标记有rel、type与href属性&#xff0c;可以指定CSS样式表的名称&#xff0c;这样就…
阅读更多...
深度学习之DCGAN

深度学习之DCGAN

目录 须知 转置卷积 DCGAN 什么是DCGAN 生成器代码 判别器代码 补充知识 LeakyReLU&#xff08;x&#xff09; torch.nn.Dropout torch.nn.Dropout2d DCGAN完整代码 运行结果 图形显示 须知 在讲解DCGAN之前我们首先要了解转置卷积和GAN 关于GAN在这片博客中已经很…
阅读更多...
攻防世界-NewsCenter

攻防世界-NewsCenter

题目信息 分析过程 题目打开是有个输入框可以用来输入搜索信息&#xff0c;初步判断是个sql注入的题目。接下来判断能否进行sql注入&#xff1a; 输入 hi&#xff0c;有搜索结果&#xff0c;如下图: 输入hi’,无结果&#xff0c;如下图&#xff1a; 初步判定是hi‘后面还有单引…
阅读更多...
【Axure高保真原型】动态伸缩信息架构图

【Axure高保真原型】动态伸缩信息架构图

今天和大家分享动态伸缩信息架构图的原型模板&#xff0c;我们可以通过点击加减按钮来展开或收起子内容&#xff0c;具体效果可以点击下方视频观看或者打开预览地址来体验 【原型效果】 【Axure高保真原型】动态伸缩信息架构图 【原型预览含下载地址】 https://axhub.im/ax9/…
阅读更多...
Python批量修改图片文件名中的指定名称

Python批量修改图片文件名中的指定名称

批量处理图像时&#xff0c;图片名有时需要统一&#xff0c;本教程仅针对图片中名如&#xff1a;0001x4.png&#xff0c;批量将图片名中的x4去除&#xff0c;只留下0001.png的情况。 如果想要按照原图片顺序批量修改图片名&#xff0c;参考其它博文&#xff1a;按照原顺序批量…
阅读更多...
SpringBoot整合rabbitmq使用案例

SpringBoot整合rabbitmq使用案例

RocketMQ&#xff08;二十四&#xff09;整合SpringBoot SpringBoot整合rabbitmq使用案例 一 SpringBoot整合RocketMQ实现消息发送和接收消息生产者1&#xff09;添加依赖2&#xff09;配置文件3&#xff09;启动类4&#xff09;测试类 消息消费者1&#xff09;添加依赖2&…
阅读更多...
Sy9-dhcp/dns服务配置

Sy9-dhcp/dns服务配置

前言、 课程需要&#xff08;进入服务器综合配置使用阶段了&#xff09;&#xff0c;这里还是沿用桌面版的ubuntu来配置dhcp和dns&#xff0c;这里updated了新的版本。2024.5 server端环境&#xff1a; Win11VMS&#xff1a;192.168.105.1192.168.105.128 &#xff08;ubuntu…
阅读更多...
AI热潮开始退去，财务压力迫使多家硅谷明星初创公司选择退出

AI热潮开始退去，财务压力迫使多家硅谷明星初创公司选择退出

曾风光无限的Stability AI已重组并削减业务规模&#xff0c;Inflection AI更是关闭业务并基本并入微软。 5月4日消息&#xff0c;国外媒体日前撰文指出&#xff0c;人工智能的热潮已开始逐渐褪去。初创公司想要同微软、谷歌等科技巨头在人工智能领域一决高下&#xff0c;门槛已…
阅读更多...
Spring IoCDI（2）—IoC详解

Spring IoCDI（2）—IoC详解

目录 一、IoC详解 1、Bean的存储 &#xff08;1&#xff09;Controller&#xff08;控制器存储&#xff09; 获取bean对象的其他方式 Bean 命名约定 &#xff08;2&#xff09;Service&#xff08;服务存储&#xff09; &#xff08;3&#xff09;Repository&#xff08…
阅读更多...
SPA模式下的多页面跳转原理及实现——jQuery Mobile为例

SPA模式下的多页面跳转原理及实现——jQuery Mobile为例

jQuery Mobile在SPA模式下的多页面跳转原理及实现案例 文章目录 jQuery Mobile在SPA模式下的多页面跳转原理及实现案例前言一、SPA的实现原理和代码分析1.实现原理说明&#xff08;1&#xff09;index.html&#xff08;2&#xff09;index.js&#xff08;3&#xff09;page2.ht…
阅读更多...
kafka日志存储

kafka日志存储

前言 kafka的主题(topic)可以对应多个分区(partition)&#xff0c;而每个分区(partition)可以有多个副本(replica)&#xff0c;我们提生产工单创建topic的时候也是要预设这些参数的。但是它究竟是如何存储的呢&#xff1f;我们在使用kafka发送消息时&#xff0c;实际表现是提交…
阅读更多...
一款开源高性能AI应用框架

一款开源高性能AI应用框架

前言 LobeChat 是一个基于 Next.js 框架构建的 AI 会话应用&#xff0c;旨在提供一个 AI 生产力平台&#xff0c;使用户能够与 AI 进行自然语言交互。 LobeChat应用架构 LobeChat 的整体架构由前端、EdgeRuntime API、Agents 市场、插件市场和独立插件组成。这些组件相互协作&a…
阅读更多...
38-1 防火墙了解

38-1 防火墙了解

一、防火墙的概念： 防火墙（Firewall)，也称防护墙，是由Check Point创立者Gil Shwed于1993年发明并引入国际互联网（US5606668 [A]1993-12-15)。它是一种位于内部网络与外部网络之间的网络安全系统，是一项信息安全的防护系统，依照特定的规则，允许或是限制传输的数据通过。…
阅读更多...
4个可将 iPhone iPad iPod 修复至正常状态的 iOS 系统恢复软件

4个可将 iPhone iPad iPod 修复至正常状态的 iOS 系统恢复软件

许多iOS用户对操作系统问题感到恐慌&#xff0c;例如iPhone卡在恢复模式、白屏死机、黑屏死机、iOS系统损坏、iTunes连接屏幕、iPhone数据丢失等。这些状态通常很无聊&#xff0c;因为您无法使用 iPhone 执行任何操作。 4个可将 iPhone iPad iPod 修复至正常状态的 iOS 系统恢复…
阅读更多...
【Unity 组件思想-预制体】

【Unity 组件思想-预制体】

【Unity 组件思想-预制体】 预制体&#xff08;Prefab&#xff09;是Unity中一种特殊的组件 特点和用途&#xff1a; 重用性&#xff1a; 预制体允许开发者创建可重复使用的自定义游戏对象。这意味着你可以创建一个预制体&#xff0c;然后在场景中多次实例化它&#xff0c;…
阅读更多...
sip转webrtc方案

sip转webrtc方案

技术选型 由于很多企业会议协议用的主要是webrtc&#xff0c;但是项目上很多时候的一些旧设备只支持sip协议&#xff0c;并不支持webrtc协议。所以sip和webrtc的相互转换就很有必要。 流媒体服务mediasoup本身并不支持sip协议。那么如何实现sip转webrtc呢&#xff1f; 根据调研…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023