文章目录
- 性能评估
- 误差
- 欠拟合和过拟合
- 模型选择与数据拟合
- 性能度量
- 二分类的混淆矩阵
- 查全率
- 查准率
- F1分数
- P-R曲线
- ROC曲线
- AUC
性能评估
机器学习的模型有很多,我们在选择的时候就需要对各个模型进行对比,这时候就需要一个靠谱的标准,能够评估模型的性能
这里的性能不是说算的有多快,而是说预测的结果和真实情况进行比较的来的结果
误差
在我们对训练的结果进行分析之前,首先需要思考模型训练过程中是否可能有误差的产生,因为这同样会影响结果和对模型选择产生比较大的影响
误差主要会出现在数据集的三个部分,分别是训练集、测试集、新样本
- 训练集——训练误差
- 测试集——测试误差
- 新样本——泛化误差
所谓的训练误差指的是训练集本身存在缺陷,从而模型提取的错误的特征信息,例如一个只认识红色苹果的模型,遇到绿色苹果时,他就不认为这是苹果了
一般情况下拿到一个数据集,会将其分成两部分,分别作为训练集和测试集,那么对于训练完成的模型,此时测试集也相当于是一个新样本
训练模型的时候,一开始训练误差和测试误差都会比较高,但是训练次数越多,训练误差会越来越小,但是测试误差可能会变大,而且模型的复杂度也会随之提升
这样的现象我们分别称之为欠拟合和过拟合
欠拟合和过拟合
欠拟合的概念很好理解,其实就是由于数据量不够大,模型的准确率不够多,也就是一开始我们学习的时候没有足够的理解一样,有时也称之为高偏差(high bias)
而过拟合则是属于过犹不及的那种感觉,就好像呆板僵化的思维,好像有些人做数学题,尽管题目非常接近,仅仅是更换了数字,但是他仍然认为这是两种完全不同的题目,这样带来的一种效果就是对于训练集(已经做过的题目)正确率很高,但是对于新样本的能力就会比较差,有时也称为高方差(high variance)
想要克服这两种现象,对于欠拟合是比较容易的,例如在决策树算法中扩展分支,在神经网络中增加训练的轮数,但是过拟合就困难的多,主要是因为模型过于复杂,我们需要的是简化模型,这种纠正策略称之为正则化(regularization)
模型选择与数据拟合
我们在模型选择时一定不能一味追求降低训练误差,因为想要有较强的数据拟合能力,就需要将模型的复杂度不断提升
也就是需要遵循一条原则,避免过拟合并且提高泛化能力
例如我们想要对一组数据想要拟合出一个多项式函数
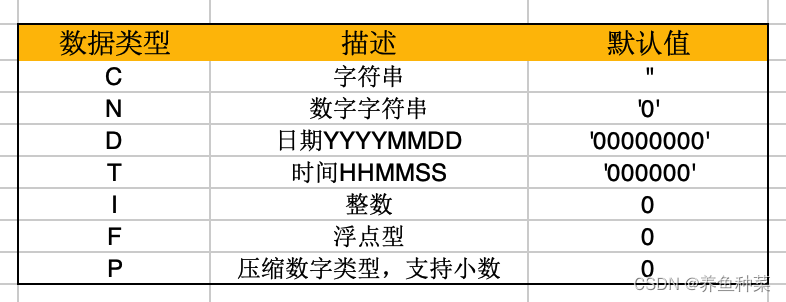
假设有一个数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x n , y n ) } T=\{(x_1,y_1),(x_2,y_2),\dots,(x_n,y_n)\} T={(x1,y1),(x2,y2),…,(xn,yn)}, x i x_i xi为样本的观测值(特征、自变量), y i y_i yi是对应的输出观测值(因变量)
我们想要找到一个m次多项式函数能够拟合这些数据,目标是能够较好拟合并且预测
设这个m次多项式函数的一般形式为: f m ( x , w ) = w 0 x 0 + w 1 x 1 + w 2 x 2 + ⋯ + w m x m = ∑ j = 0 m w j x j f_m(x,w)=w_0x^0+w_1x^1+w_2x^2+\dots+w_mx^m=\sum_{j=0}^{m}w_jx^j fm(x,w)=w0x0+w1x1+w2x2+⋯+wmxm=∑j=0mwjxj
对于这个公式的解读:
- 有m+1个特征值,x的次数从0到m
- 有m+1个需要通过训练(学习)得到的权值参数,w的下标从0到m
- 这里参数的正负,绝对值大小就分别代表了对于这个特征的态度,绝对值越大权重越大
- 可以有意识的调整某些权值让他趋近于0,从而抛弃某些特征,称之为权重衰减(weight decay),在某种程度上可以避免过拟合
那如何训练学习这个m+1个参数呢,常用的策略之一是最小二乘法(Method of Least Squares)
通过这个方法拟合出来的函数值 f ( x i , w ) f(x_i,w) f(xi,w)(得到的预测结果)和真实的 y i y_i yi是由误差的,数学上称之为残差(residual)
e i = f ( x i , w ) − y i e_i=f(x_i,w)-y_i ei=f(xi,w)−yi
高斯证明了,在这个残差集合独立同分布的假定下,最小二乘法有一个优势,就是在所有的无偏线性估计类中方差最小,也就是当残差的平方和最小时,拟合函数的相似度最高,也就是如下函数取最小值时,拟合效果最好
L ( w ) = 1 2 ∑ i = 1 n ( f ( x i , w ) − y i ) 2 L(w)=\frac{1}{2}\sum_{i=1}^{n}(f(x_i,w)-y_i)^2 L(w)=21∑i=1n(f(xi,w)−yi)2
性能度量
上面我们讲到的其实是性能评估的一般思路,接下来我们就需要找到一个标准,能够确切的评判性能的高低了
二分类的混淆矩阵
二值分类器(Binary Classifier)是在机器学习中应用最广泛的分类器之一,二值分类指的是正类和负类,我们为了方便陈述称之为真和假
主要分四类
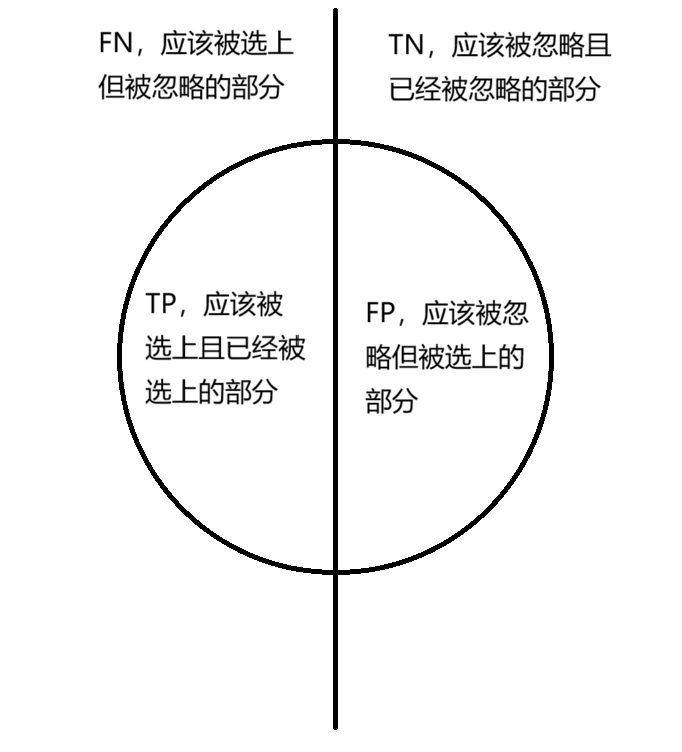
- 真正类(True Positive,TP),实际为真,被模型预测为真,为了方便理解,我们说他是应该被选上且已经被选上了的
- 假正类(False Positive,FP),实际为假,被模型预测为真,应该没被选上(被忽略)但是被选上了的
- 真负类(True Negative,TN),实际为假,被模型预测为假,应该被忽略且已经被忽略了的
- 假负类(False Negative,FN),实际为真,被模型预测为假,应该被忽略但被选上了的
这四类加起来就是总样本数,然后第一类和第三类是正确预测了的,第二类和第四类是预测失误了的,分别称之为误报、第一类错误,漏报、第二类错误
这四组样本就构成了混淆矩阵(confusion matrix),确实容易混淆
由这四组样本就能产生一些比例作为判断,再通过这些比例之间的关系,我们就能找到更优的模型了
主要有以下几个,查全率,查准率,F1分数,P-R曲线,ROC曲线
我们尽量避免过于不说人话的描述,用最简单容易理解的话来讲清楚这些概念
在说这些概念之前,我们先画一个简单的示意图,可以配合起来理解
查全率
查全率(Recall,R,召回率),表示分类准确的正类样本数占全部正类样本数的比例,说人话就是在所有应该被选上的样本中,选上了的比例是多少,也就是左边那一半TP占的比例 R = T P T P + F N R=\frac{TP}{TP+FN} R=TP+FNTP
查准率
查准率(Precision,P),表示被预测正确的正类样本数占分类器判定为正类样本总数的比例,说人话就是所有被选上的样本中,选对了的样本比例是多少,也就是这个圆里面左边占的部分比例 P = T P T P + F P P=\frac{TP}{TP+FP} P=TP+FPTP
需要注意的是,查准率和准确率是有区别的,准确率应该是正确判断的样本除总样本得到的比例
一般来说查准率和查全率是呈负相关的,那有没有可以兼顾这样两个比率的呢,或者说有没有一个值可以用来调整他们之间的比重关系
F1分数
本质上来说F1分数是查准率和查全率的调和平均数
1 F 1 = 1 2 ( 1 P + 1 R ) \frac{1}{F1}=\frac{1}{2}(\frac{1}{P}+\frac{1}{R}) F11=21(P1+R1)整理一下就是 F 1 = 2 × P × R P + R F1=2\times\frac{P\times R}{P+R} F1=2×P+RP×R
想要有所偏向,就可以引入参数 β \beta β
1 F β = 1 1 + β 2 ( 1 P + β 2 R ) \frac{1}{F_\beta}=\frac{1}{1+\beta^2}(\frac{1}{P}+\frac{\beta^2}{R}) Fβ1=1+β21(P1+Rβ2)整理一下就是 F β = ( 1 + β 2 ) 1 1 P + β 2 R F_\beta=(1+\beta^2)\frac{1}{\frac{1}{P}+\frac{\beta^2}{R}} Fβ=(1+β2)P1+Rβ21
当 β > 1 \beta>1 β>1时, β 2 R \frac{\beta^2}{R} Rβ2项占比较大,即查全率的影响更大,反之则查准率的影响更大
P-R曲线
P-R曲线其实很简单,因为查准率和查全率大致成负相关,就可以分别将查全率和查准率作为坐标轴画出图形,那么这其中变化的是什么呢,其实就是我们设定的临界值,之后的ROC曲线也是类似,选取的标准不同,查全率和查准率的数值也会不同
当两个模型的P-R曲线都绘制出来之后,我们就可以根据曲线进行抉择了
第一种情况是一个模型的曲线完全在另一个曲线的上方,也就是查全率和查准率都高于另一个,那就直接选了
但是更通常的情况是交替出现,这时候就有一个所谓的平衡点(Break-Even Pont、BEP),就是y=x这条直线和两条曲线的交点,一般认为谁的交点在上方,谁就更优
P-R曲线的优点是非常直观,但是缺点也很明显,受样本分布的影响非常大
于之相比,ROC曲线就相对更优,也因此作为重要的指标之一
ROC曲线
于P-R曲线对应的,ROC曲线的横纵坐标也是两个比率
第一个比率是真阳性率(True Positive Rate,TPR),简单说就是应该被忽略但没有被忽略的占比, T P R = F P T N + F P TPR=\frac{FP}{TN+FP} TPR=TN+FPFP
第二个比率是假阳性率(False Positive Rate,FPR),简单说就是应该被选中并且已经被选中的占比, F P R = T P T P + F N FPR=\frac{TP}{TP+FN} FPR=TP+FNTP
把假阳性率作为横轴,真阳性率作为纵轴,就能画出ROC曲线了,并且变化的仍然是选取的标准不同
现在已经绘制出了对应的ROC曲线了,应该如何选取更优的模型呢
AUC
AUC是Area Under Curve,意思是曲线下的区域,那其实就是ROC曲线与X轴的面积
一般认为AUC在0.5到1之间,如果不在这个范围内,只需要将模型的预测概率P反转成1-P就能得到一个更好的分类器
并且AUC的值越高,我们认为这个模型就越优