未完待续，填坑ing……

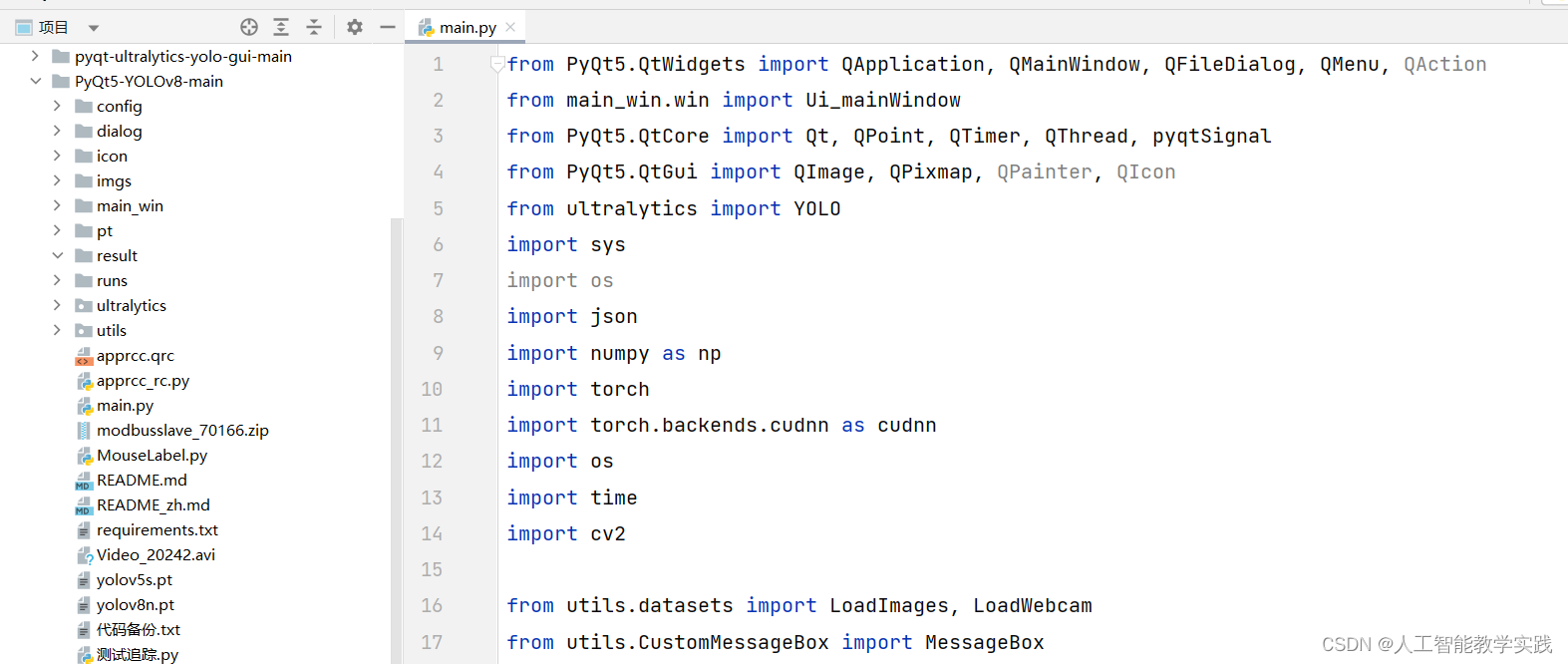
魔方操作的表示——辛马斯特标记

辛马斯特标记（Singmaster Notation）是一种用于描述魔方和类似拼图的转动操作的标记系统。它以大卫·辛马斯特（David Singmaster）的名字命名，辛马斯特标记系统使用单个字符来代表特定的转动动作。

魔方状态数

不考虑复原的组合数

首先，如果有魔方拆装并尝试复原经验，可以知道并不是每次把魔方拆了再装回去都可以复原的。先不考虑是否可以复原，单纯用排列组合计算三阶魔方的状态数：

1. 8个角块，有8! 个位置的排列组合；在每个位置上，角块有3种方向，共3^8种方向
2. 12个棱块，有12! 个位置的排列组合；在每个位置上，棱块有2种方向，共2^12种方向

所以不考虑复原时，共有这么多种状态：
$8!\times 3^8\times 12!\times 2^{12}=519,024,039,293,878,272,000$

考虑复原的组合数

为什么随便拼装的魔方不一定可以复原呢，因为魔方从一个复原的状态，经过合法的转动后，到达不了这些无法复原的状态，这是最朴素的想法。

实际上，魔方是一个群，而且是一个置换群。

群的定义

在抽象代数中，群是一种代数结构，它由一个集合以及在这个集合上定义的一个二元运算组成。一个群需要满足以下四个条件，这些条件通常被称为群的公理：

1. 封闭性：对于群G中的任意两个元素a和b，它们的组合ab也必须属于G。
2. 结合律：对于群G中的任意三个元素a、b和c，组合(ab)c和a(bc)得到的结果必须相等。
3. 存在单位元：群G中存在一个元素e，对于任意元素a，都有ae = ea = a。
4. 存在逆元：对于群G中的任意元素a，存在一个元素b，使得ab = ba = e，其中e是群G的单位元。

当我们将群的定义应用于自然数集合（包括0）和加法运算时，我们得到了一个典型的例子。

1. 封闭性：对于任意两个自然数a和b，它们的和a + b也是一个自然数，因此加法在自然数集合上是封闭的。
2. 结合律：对于任意三个自然数a、b和c，有(a + b) + c = a + (b + c)，因此加法满足结合律。
3. 存在单位元：自然数集合中的单位元是0，对于任意自然数a，有a + 0 = 0 + a = a。
4. 存在逆元：对于任意自然数a，存在一个逆元-b，使得a + (-a) = (-a) + a = 0。

因此，自然数集合和加法运算构成了一个满足群的所有条件的代数结构。

置换群的定义

简而言之，如果有一个群S，对群中元素作不同的映射得到不同的新群，且这些新群之间又满足群的定义，那么群S就是置换群。

---

例：
假如有一个三角形，构成一个群S：

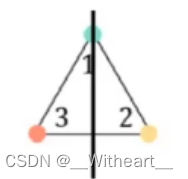
对其进行旋转（0°、120°、240°），翻转（沿12、沿13、沿23）操作，得到：

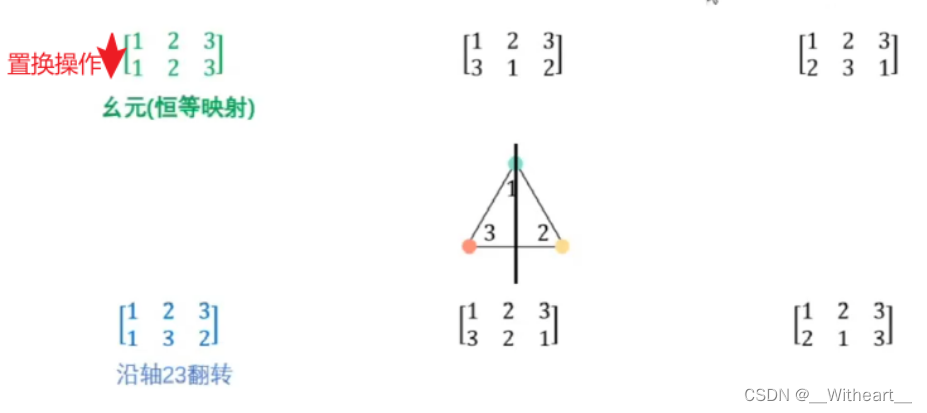
这些操作本身也符合群的定义：操作之间符合封闭性、结合律、有幺元和逆元

那么群S就称之为置换群

奇置换和偶置换

1. 偶置换是指包含偶数个置换的置换，而奇置换则是指包含奇数个置换的置换。
2. 在一个置换群中，奇置换和偶置换构成了两个不相交的子集。

• 置换的复合
  两个偶置换的复合是偶的
  两个奇置换的复合是偶的
  一个奇置换与偶置换的复合是奇的

一个奇置换的例子：

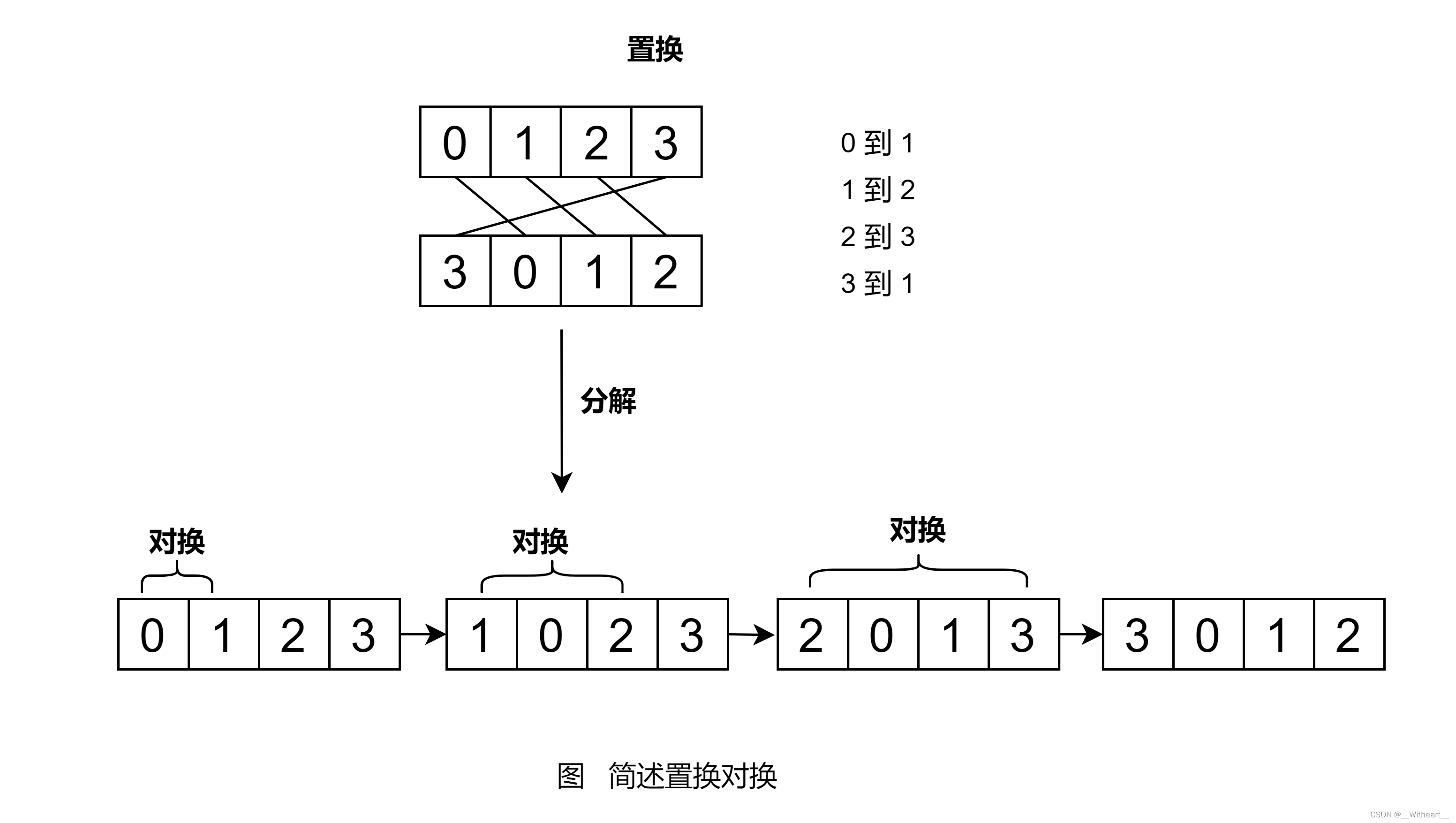
来自：https://blog.csdn.net/weixin_46645613/article/details/117479516

上图中讲述两个排列怎么发生的置换操作，应该很清楚明了了，这在数学中记为$\left(\begin{array}{cccc}1& 2& 3& 4\\ 4& 1& 2& 3\end{array}\right)=(12)(13)(14)$，表示这个置换可以分解成 3 次对换，所以是一个奇置换。也可以这么看，只经过一次对换操作是奇置换，上述置换由 3 个奇置换复合，所以合起来也为奇置换。

魔方与置换群

• 对魔方进行一次90度的旋转，$\left(\begin{array}{c}012\\ 345\\ 789\end{array}\right)->\left(\begin{array}{c}730\\ 841\\ 952\end{array}\right)$，也就是四个角块顺时针旋转（3次置换），四个棱块顺时针旋转（3次置换），共6次置换，是偶置换

也就是说，从魔方复原的状态进行合法的旋转，都是进行偶置换，而在一个置换群中，奇置换和偶置换构成了两个不相交的子集，所以魔方随意组装的时候只有1/2的概率可以通过合法旋转复原。

同时易知，魔方无法通过合法旋转交换单独一对棱块或者角块而不影响其他棱块和角块的位置，因为单独交换是一种奇置换，而魔方旋转是偶置换。

考虑复原的组合数

不能复原的情况有

1. 单棱翻转（1/2）——单独翻转这个棱块是一个奇置换
2. 单角块翻转（2/3）——单独翻转这个角块是一个奇置换
3. 单棱块位置翻转（1/2）——单独交换这两个棱块的位置是一个奇置换

问：为什么只有棱块会出现只交换一对棱块的情况，角块不会出现只交换一对角块的情况吗？

https://www.zhihu.com/tardis/bd/art/57444167
A：这个问题很好，角块一样也会出现只交换一对角块的情况，但是学过PLL公式的同学都知道，角块和棱块交换情况是可以互相转换的（例如PLL邻角对棱换）。所以角块错误的情况可以转化为棱块的错误情况

所以考虑复原的状态数要在不考虑复原的组合数基础上，乘以能复原的情况概率
$(1-1/2)\times (1-2/3)\times (1-1/2)=1/12$

为：
$\frac{3^8\times 8!\times 2^{12}\times 12!}{12}=43,252,003,274,489,856,000$

魔方棱块角块方向的定义

这里使用 kociemba 二阶段算法来进行方向的的定义

---

首先规定：
U黄
D白
F红
B橙
L蓝
R绿

• UD颜色为高级色、LR颜色为次高级色

棱块

参照色的选择

• 如果一个棱块含黄色或者白色的两种高级色（意味着其为U或者D的棱块），那么使用其含有的高级色作为其参照色
• 如果不含高级色只含次高级色，那么使用次高级色作为参照色

根据参照色及位置进行方向的确定

• 当棱块位于顶层或者底层，那么如果参照色也位于顶层或者底层，则该棱块规定方向为0，否则为1
• 当棱块位于中间层，那么当参照色位于次高级面，则规定该棱块方向为1，否则为0

对于上面这张图来说，上面的棱块参照色为高级色白色，且参照色在高级色面U上，所以方向为0；而下面的棱块参照色为次高级色绿色，且参照色在次高级色面R上，所以方向也为0。

而对这张图来说，进行了一次旋转。此时上面的棱块参照色是绿色次高级色，其位于顶层但是参照色不位于顶层，所以方向为1；而下面的棱块的参照色是白色高级色，其位于中间层但是参照色不位于次高级面L或者R，所以方向也为1。

角块

也规定顶层底层为高级层，颜色为高级色

---

由于角块一定含有顶层或者底层颜色，故将其顶层或者底层颜色规定为参照色，根据参照色与高级层的相对位置对方向进行规定：

• 只要参照色在高级层上，角块方向为0
• 参照色相对高级层顺时针扭转，角块方向为1
• 参照色相对高级层逆时针扭转，角块方向为2

如上图，白色为参照色，其位于顶层，高级面为黄色。

• 最左边魔方角块参照色在高级面上，这个角块方向为0
• 中间魔方角块参照色相对高级面顺时针旋转，这个角块方向为1
• 最右边魔方角块参照色相对高级面逆时针旋转，这个角块方向为2

kociemba二阶段算法

kociemba二阶段算法是一种降群法。

• 一阶段：将魔方角块方向、棱块方向都归0，且中层的棱块只位于中层
• 二阶段：将角块、顶底层棱块、中间棱块归位

一阶段方向归零

可用的操作有：U,R,F,D,L,B

如何保证二阶段求解时角块棱块方向不变

对于使用了kociemba定义方向的魔方来说：

• 角块方向：只有U、D层的旋转不改变角块方向
• 棱块方向：规定了次高级面后，次高级面的旋转会改变棱块方向，如（L、R），但是如果旋转两次（L2、R2）改变两次棱块方向，相当于棱块方向没改变；而非次高级面（F、B）的旋转并不改变棱块方向

次高级面可以规定为(L、R)或者(F、B)

---

所以，二阶段如果要在一阶段方向都归零的情况下对棱块和角块进行归位，可用的操作只有U,D,L2,R2,F2,B2。

搜索算法

kociemba 使用 IDA* 算法进行搜索。

A*算法

A* 算法，就是一种考虑了实际代价和估计代价的BFS。其在每一种状态下计算所有可能的操作的代价，代价小的优先搜索。

常被用于解决八数码问题，详情看我这篇文章：八数码问题——A*算法的应用（A-Star）

IDA*算法

IDA*算法，是一种有限制搜索深度的DFS。其设定好一个限制，在一种状态下计算其一种可能的操作代价，然后进入下一个状态并继续计算再下一个状态，直到深度到达设定的限制。在到达限制之前，如果找到目标，直接返回；如果到达限制了还没找到目标，则返回上一个节点，进行其他分支的深度搜索。

IDA算法适用于状态空间特别大的问题。因为这类问题的状态空间过大，使用BFS需要一次性扩展所有当前层的节点，这可能会导致搜索空间过大，耗费大量时间和计算资源；而IDA算法可以通过迭代加深搜索的方式逐渐扩大搜索范围，减少搜索时间和占用内存。

• IDA*算法框架

# 定义一个全局变量，用于表示无穷大的值
INFINITY = 999999999

# IDA*算法的入口函数
function IDA_Star(root):
    # 初始化阈值为启发式函数计算的代价
    bound = heuristic_cost(root)
    while True:
        # 调用search函数进行搜索
        t = search(root, 0, bound)
        # 如果找到目标状态，返回结果
        if t == FOUND:
            return FOUND
        # 如果搜索范围超出限制，返回未找到
        if t == INFINITY:
            return NOT_FOUND
        # 更新阈值
        bound = t

# IDA*算法的搜索函数
function search(node, g, bound):
    # 计算当前节点的f值（g + 启发式函数值）
    f = g + heuristic_cost(node)
    # 如果f值超过阈值，返回f值
    if f > bound:
        return f
    # 如果当前节点是目标状态，返回找到目标
    if node is goal:
        return FOUND
    # 初始化一个最小代价为无穷大的值
    min = INFINITY
    # 遍历当前节点的后继节点
    for each successor in generate_successors(node):
        # 递归搜索后继节点
        t = search(successor, g + cost(node, successor), bound)
        # 如果找到目标状态，返回找到目标
        if t == FOUND:
            return FOUND
        # 更新最小代价
        if t < min:
            min = t
    # 返回最小代价
    return min