抛砖引玉
在深度学习中，优化算法是训练神经网络时至关重要的一部分。
优化算法的目标是最小化（或最大化）一个损失函数，通常通过调整神经网络的参数来实现。
这个过程可以通过梯度下降法来完成，其中梯度指的是损失函数关于参数的偏导数。
本文将介绍一阶优化算法和二阶优化算法，并详细讲解常用的梯度下降法，包括梯度下降法、随机梯度下降法、动量法、AdaGrad、RMSProp和Adam。
一阶优化算法
一阶优化算法主要根据损失函数的一阶导数（梯度）来更新模型参数。常见的一阶优化算法包括梯度下降法、随机梯度下降法、动量法等。
1. 梯度下降法（Gradient Descent）
梯度下降法是最基本的优化算法之一，它通过计算损失函数关于参数的梯度，并沿着梯度的反方向更新参数，从而使损失函数不断减小。
因为这里的损失函数是在整个数据集上进行计算得到的均值，所以每更新一次模型参数，就要对整个数据集进行一个计算，可想而知这样非常的慢，并且当数据集变得非常大的时候，如此多的数据没法都load到内存中。
void gradient_descent(float *params, float *gradients, float learning_rate, int n)
{
for (int i = 0; i < n; i++)
{
params[i] -= learning_rate * gradients[i];
}
}
2. 随机梯度下降法（Stochastic Gradient Descent）
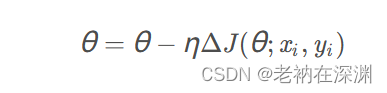
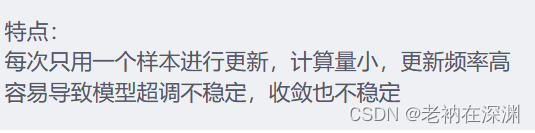
随机梯度下降法和梯度下降法其实是走的两个极端，梯度下降法是每次更新都计算整个数据集的loss，而随机梯度下降法每次更新都只用了一对样本，即上面公式中的一对样本(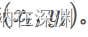
由于每个样本都会对模型进行更新，所以模型更新的特别频繁，参数就会变成高方差，损失函数的波动也会有很大强度的变化。有时候，这是好事，因为这样的可以帮助我们探索新的更新方向，找到更加好的局部极值点。但是，由于频繁的更新和波动，会导致模型的损失收敛的非常不稳定。
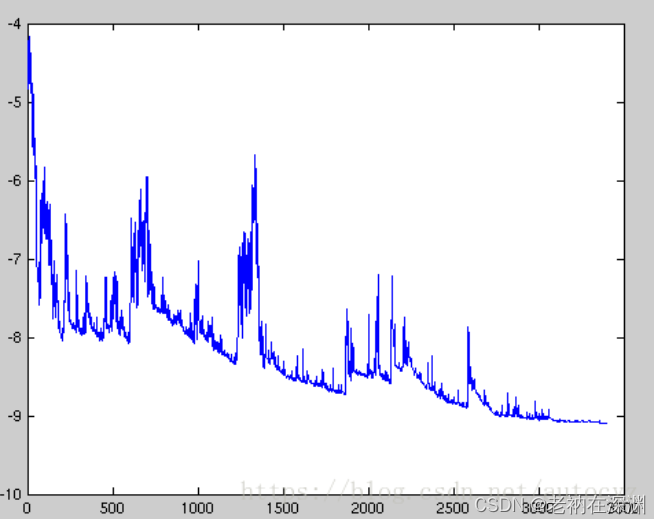
上图就是随机梯度下降法更新过程中loss值的变化，可以发现loss值的变化非常大，这就是模型超调了，整个模型比较不稳定
随机梯度下降法是梯度下降法的一种变种，它在每次迭代中随机选取一部分样本来计算梯度，从而加快了训练速度。
void stochastic_gradient_descent(float *params, float *gradients, float learning_rate, int n)
{
for (int i = 0; i < n; i++)
{
params[i] -= learning_rate * gradients[i];
}
}
3. 动量法（Momentum）
带momentum(动量)的梯度下降法也是一种很常用的的优化算法。这种方法因为引入了momentum量，所以能够对梯度下降法起到加速的作用。
打个比方，一个球顺着斜坡往下滚动，会因为地心引力的原因而一直加速，速度越来越快的往坡低滚去。梯度下降法中的Momentum量就和地心引力的作用很类似，能够让梯度下降法沿着下降的方向逐渐扩大幅度。起到对梯度下降法进行加速的作用。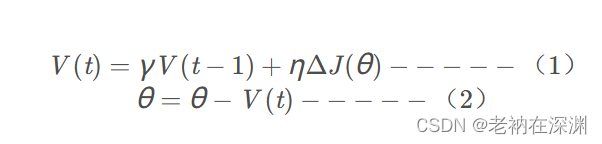
从上述公式（1）可以看出，当当前的梯度方向
的正负号）和
的方向相同时，
所以参数 θ 的变化幅度会增大，从而加快梯度下降法的幅度；而当方向不同时，会逐步减小当前更新的幅度。这样可以有效的对梯度下降法进行加速，同时提高模型的稳定性。
动量法通过引入动量项来加速收敛过程，它模拟了物体运动时的惯性，可以减少梯度更新的波动，从而加快了训练速度。
void momentum(float *params, float *gradients, float learning_rate, float momentum_rate, float *velocities, int n) {
for (int i = 0; i < n; i++) {
velocities[i] = momentum_rate * velocities[i] + learning_rate * gradients[i];
params[i] -= velocities[i];
}
}
二阶优化算法
二阶优化算法基于损失函数的二阶导数（Hessian矩阵）来更新模型参数。常见的二阶优化算法包括AdaGrad、RMSProp和Adam。
1. AdaGrad
在mini batch梯度下降法中，因为对所有的参数均使用相同的学习率，而当有的参数的梯度很大，有的很小时，显然不合适。另外，对于不同的样本，如果有的样本出现的较为频繁，导致其对应的一些参数更新较为频繁，而有的样本出现的频率很低，导致一些参数更新频率很低时，再采用相同的学习率有时候也不太合适。我们更加希望那些出现更新频率比较低的参数能够有更大的更新幅度。
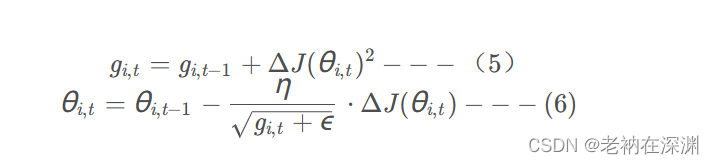
AdaGrad算法通过动态调整学习率来提高收敛速度，它根据参数的历史梯度调整学习率，对于频繁出现的参数会降低学习率，对于不经常出现的参数会增加学习率。
void adagrad(float *params, float *gradients, float learning_rate, float epsilon, float *accumulators, int n)
{
for (int i = 0; i < n; i++)
{
accumulators[i] += gradients[i] * gradients[i];
params[i] -= learning_rate * gradients[i] / (sqrt(accumulators[i]) + epsilon);
}
}
2. RMSProp
RMSProp算法是对AdaGrad算法的改进，它通过引入一个衰减系数来控制历史梯度的衰减速度，从而减少了学习率的波动。
void rmsprop(float *params, float *gradients, float learning_rate, float decay_rate, float epsilon, float *accumulators, int n)
{
for (int i = 0; i < n; i++)
{
accumulators[i] = decay_rate * accumulators[i] + (1 - decay_rate) * gradients[i] * gradients[i];
params[i] -= learning_rate * gradients[i] / (sqrt(accumulators[i]) + epsilon);
}
}
3. Adam
前面我们从最经典的梯度下降法开始，介绍了几个改进版的梯度下降法。
Momentum方法通过添加动量，提高收敛速度；
Nesterov方法在进行当前更新前，先进行一次预演，从而找到一个更加适合当前情况的梯度方向和幅度；
Adagrad让不同的参数拥有不同的学习率，并且通过引入梯度的平方和作为衰减项，而在训练过程中自动降低学习率；
AdaDelta则对Adagrad进行改进，让模型在训练后期也能够有较为适合的学习率。
Adam算法是一种结合了动量法和RMSProp算法的优化算法，它不仅考虑了梯度的一阶矩（均值），还考虑了梯度的二阶矩（方差），从而更加准确地更新参数。
void adam(float *params, float *gradients, float learning_rate, float beta1, float beta2, float epsilon, float *m, float *v, int t, int n) {
for (int i = 0; i < n; i++)
{
m[i] = beta1 * m[i] + (1 - beta1) * gradients[i];
v[i] = beta2 * v[i] + (1 - beta2) * gradients[i] * gradients[i];
float m_hat = m[i] / (1 - pow(beta1, t));
float v_hat = v[i] / (1 - pow(beta2, t));
params[i] -= learning_rate * m_hat / (sqrt(v_hat) + epsilon);
}
}
代码实现
下面是一个简单示例，演示了如何使用上述优化算法训练一个简单的线性回归模型。
#include <iostream>
#include <cmath>
void gradient_descent(float *params, float *gradients, float learning_rate, int n)
{
for (int i = 0; i < n; i++)
{
params[i] -= learning_rate * gradients[i];
}
}
void stochastic_gradient_descent(float *params, float *gradients, float learning_rate, int n)
{
for (int i = 0; i < n;```cpp
i++) {
params[i] -= learning_rate * gradients[i];
}
}
void momentum(float *params, float *gradients, float learning_rate, float momentum_rate, float *velocities, int n)
{
for (int i = 0; i < n; i++)
{
velocities[i] = momentum_rate * velocities[i] + learning_rate * gradients[i];
params[i] -= velocities[i];
}
}
void adagrad(float *params, float *gradients, float learning_rate, float epsilon, float *accumulators, int n)
{
for (int i = 0; i < n; i++)
{
accumulators[i] += gradients[i] * gradients[i];
params[i] -= learning_rate * gradients[i] / (sqrt(accumulators[i]) + epsilon);
}
}
void rmsprop(float *params, float *gradients, float learning_rate, float decay_rate, float epsilon, float *accumulators, int n)
{
for (int i = 0; i < n; i++)
{
accumulators[i] = decay_rate * accumulators[i] + (1 - decay_rate) * gradients[i] * gradients[i];
params[i] -= learning_rate * gradients[i] / (sqrt(accumulators[i]) + epsilon);
}
}
void adam(float *params, float *gradients, float learning_rate, float beta1, float beta2, float epsilon, float *m, float *v, int t, int n)
{
for (int i = 0; i < n; i++)
{
m[i] = beta1 * m[i] + (1 - beta1) * gradients[i];
v[i] = beta2 * v[i] + (1 - beta2) * gradients[i] * gradients[i];
float m_hat = m[i] / (1 - pow(beta1, t));
float v_hat = v[i] / (1 - pow(beta2, t));
params[i] -= learning_rate * m_hat / (sqrt(v_hat) + epsilon);
}
}
int main()
{
// 参数初始化
float params[2] = {0};
float gradients[2] = {0};
float velocities[2] = {0};
float accumulators[2] = {0};
float m[2] = {0};
float v[2] = {0};
// 数据初始化
float x[5] = {1, 2, 3, 4, 5};
float y[5] = {2, 4, 6, 8, 10};
// 学习率
float learning_rate = 0.01;
// 动量因子
float momentum_rate = 0.9;
// AdaGrad参数
float epsilon_adagrad = 1e-8;
// RMSProp参数
float decay_rate_rmsprop = 0.9;
float epsilon_rmsprop = 1e-8;
// Adam参数
float beta1_adam = 0.9;
float beta2_adam = 0.999;
float epsilon_adam = 1e-8;
// 训练
int epochs = 100;
int n = 2;
for (int epoch = 1; epoch <= epochs; epoch++) {
float loss = 0;
for (int i = 0; i < 5; i++) {
float prediction = params[0] * x[i] + params[1];
float error = prediction - y[i];
loss += error * error;
gradients[0] = 2 * error * x[i];
gradients[1] = 2 * error;
// 使用各种优化算法更新参数
// gradient_descent(params, gradients, learning_rate, n);
// stochastic_gradient_descent(params, gradients, learning_rate, n);
// momentum(params, gradients, learning_rate, momentum_rate, velocities, n);
// adagrad(params, gradients, learning_rate, epsilon_adagrad, accumulators, n);
// rmsprop(params, gradients, learning_rate, decay_rate_rmsprop, epsilon_rmsprop, accumulators, n);
adam(params, gradients, learning_rate, beta1_adam, beta2_adam, epsilon_adam, m, v, epoch, n);
}
loss /= 5;
std::cout << "Epoch " << epoch << ", Loss = " << loss << ", Params = " << params[0] << ", " << params[1] << std::endl;
}
return 0;
}
这段代码演演示了实现梯度下降法、随机梯度下降法、动量法、AdaGrad、RMSProp和Adam等优化算法来训练一个简单的线性回归模型
总结 Gradient Descent Algorithm
Gradient Descent is one of the fundamental optimization algorithms used in machine learning and deep learning. It is used to minimize a loss function by iteratively adjusting the parameters of a model. The basic idea behind Gradient Descent is to compute the gradient of the loss function with respect to the model’s parameters and update the parameters in the opposite direction of the gradient to minimize the loss.
Algorithm Steps:
-
Initialize Parameters: Start by initializing the parameters of the model with random values.
-
Compute Gradients: Compute the gradient of the loss function with respect to each parameter of the model using backpropagation.
-
Update Parameters: Update the parameters of the model using the following update rule:
-
-
Repeat: Repeat steps 2 and 3 until the loss converges to a minimum or for a fixed number of iterations.
Pseudocode:
function gradient_descent(params, gradients, learning_rate):
for each parameter theta in params:
theta = theta - learning_rate * gradient
Implementation in C++:
void gradient_descent(float *params, float *gradients, float learning_rate, int n) {
for (int i = 0; i < n; i++) {
params[i] -= learning_rate * gradients[i];
}
}
Conclusion:
Gradient Descent is a powerful optimization algorithm used to train machine learning and deep learning models. It is simple to implement and computationally efficient, making it the go-to choice for optimizing a wide range of models.
