计数排序，基数排序，桶排序

计数排序:

基数排序：

桶排序:

计数排序:

计数排序是一种非比较型整数排序算法，特别适用于一定范围内的整数排序。它的核心思想是使用一个额外的数组（称为计数数组）来计算每个值的出现次数，然后根据这些计数信息将所有的数字放到正确的位置上，从而实现排序。

大致流程就是这样的，我会用图和代码的思想给大家讲清楚的：

确定范围：首先遍历一遍待排序的数组，找出其中最大值和最小值，从而确定数字的范围。这是因为计数排序要求输入数据在一个已知的有限范围内。
初始化计数数组：创建一个长度为最大值与最小值之差加一的计数数组，并将所有元素初始化为0。计数数组的索引代表原始数组中的数值，值则表示该数值出现的次数。
计数：再次遍历原始数组，对于每个元素，将计数数组中对应索引的值加一，即统计每个元素出现的次数。
累加计数：对计数数组进行累加操作，使得计数数组中的每个元素变成小于等于其索引值的所有元素的累计总和。这样，计数数组中的每个位置就表示了在排序后数组中相应数值的起始位置。
重建数组：最后，从计数数组反向遍历原始数组，根据计数数组的信息将元素放到排序后数组的正确位置上。当把一个元素放到排序后数组时，相应地减少计数数组中该元素的计数，以保持计数的准确性。

第一步：创建一个数组，并且找到其中的最大值和最小值

第二步：定义一个count数组(最大值减去最小值加一)，用来统计每个数字出现的次数

第三步：遍历count数组，然后按照大小顺序把依次放回array数组里面去(可以理解成覆盖了原数组)，最后出来的结果就可以按照大小顺序看到每一个数字出现的多少次

最后出来的结果就是：[1, 1, 2, 3, 4, 5, 5, 6, 8, 9, 9]

public static int[] countSort(int[] array){
        int minval = array[0];
        int maxval = array[0];
        for(int i = 0;i<array.length;i++){
            if(array[i] < minval){
                minval = array[i];
            }
            if(array[i] > maxval){
                maxval = array[i];
            }
        }
        int[] count = new int[maxval-minval+1];
        for(int i = 0;i<array.length;i++){
            int val = array[i];
            count[val-minval]++;
        }
        //遍历计数数组
        int index = 0;
        for(int i = 0;i<count.length;i++){
            while(count[i]>0){
                array[index] = i+minval;
                index++;
                count[i]--;
            }
        }
        return array;
    }

时间复杂度:

计数排序的时间复杂度主要由两部分组成：统计每个元素出现次数和根据统计结果重构输出数组。对于n个元素，范围在0到k之间的整数排序，计数排序的时间复杂度为O(n+k)。其中，n是数组长度，k是数组中最大值与最小值的差加1。在最好的情况下（即k接近n或n），时间复杂度接近线性，但在k远大于n时，时间复杂度会显著增长。

空间复杂度:

计数排序需要额外的空间来存储每个元素的计数，这个空间取决于待排序数组中元素的范围。具体来说，需要一个大小为k+1的计数数组，其中k是数组中的最大值与最小值之差加1。因此，空间复杂度为O(k)。如果k与n同数量级，那么空间复杂度也是线性的，即O(n)。

稳定性:

计数排序是一种稳定的排序算法。因为它在统计每个元素的频率之后，按照元素原来的顺序（通过第二个循环从最小元素开始逐个累加计数数组并放回原数组）将元素放回原数组，保证了相同元素的相对位置不会改变。

基数排序：

它的核心思想是将待排序的元素根据其每一位的数值进行分配，这个过程通常从最低有效位（LSD）开始，也可以从最高有效位（MSD）开始，然后按位递进，直到最高位。基数排序利用了分配式排序的策略，也被称为“桶排序”的一种推广。

第一步:首先得有一个数组然后才能对数组进行排序，找到数组中的最大值，确定最大值的位数，比如198就是3位数

第二步：新建一个buckets数组，根据个位十位百位...来存放数据

1.按照个位数排序就是这样的，然后我们按照先进先出的原则拿出来

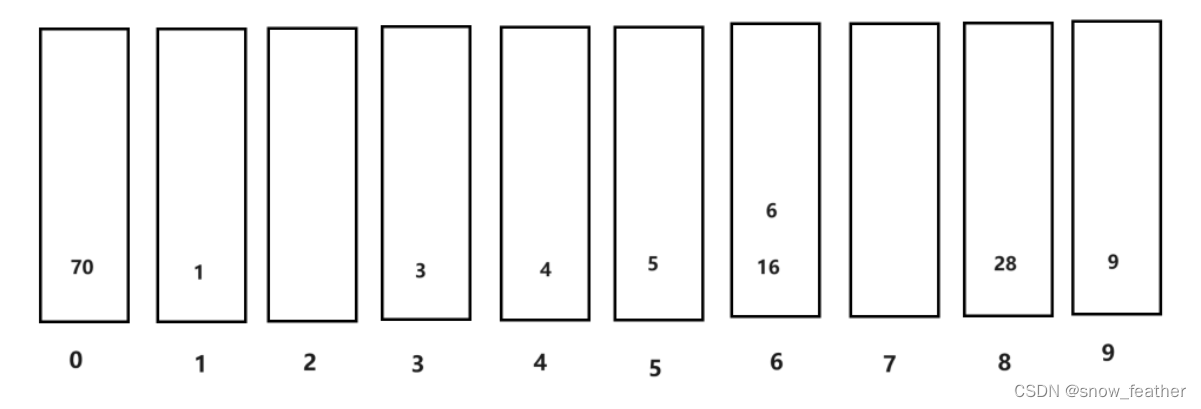
2.此时的buckets数组就是：

3.因为最大为2位数，所以我们还得再进行一个十位的比较

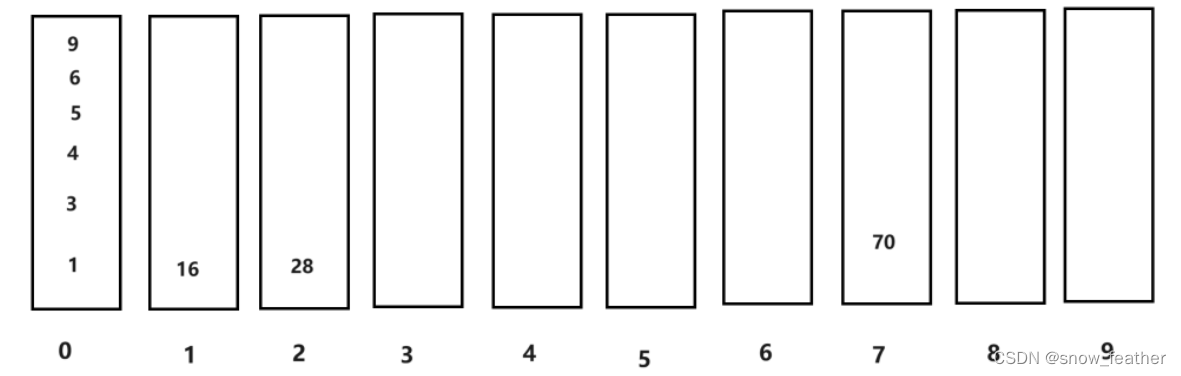
4. 按照先进先出的原则拿出来就得到最终结果：

private static int getMaxDigits(int[] array){
    int maxnum = array[0];
    for(int num : array){
        if(num > maxnum){
            maxnum = num;
        }
    }
    return (int)Math.log10(maxnum)+1;
}

public static int[] radixSort(int[] array){
    int maxnum = getMaxDigits(array);
    int radix = 10;//基数是10 因为是10进制
    List<Integer>[] buckets = new ArrayList[radix];
    for(int i = 0;i < radix;i++){
        buckets[i] = new ArrayList<>();
    }

    for(int digit = 1;digit <= maxnum;digit++){

        //记得每次要把桶清空
        for (List<Integer> bucket : buckets) {
            bucket.clear();
        }

        for (int num : array) {
            int index = (num / (int)Math.pow(10,digit-1))%10;
            buckets[index].add(num);
        }

        //从桶中收集元素到数组
        int index = 0;
        for(List<Integer> bucket : buckets){
            for(int num : bucket){
                array[index] = num;
                index++;
            }
        }
    }
    return array;
}

时间复杂度:

基数排序的时间复杂度主要取决于数字的位数（d，即最大数的位数）和待排序元素的数量（n）。
最好、平均和最坏情况下，基数排序的时间复杂度都是O(d*(n+k))，其中k是基数（通常是10，因为基数排序常用于十进制数）。这意味着排序的总成本是元素数量乘以位数，加上每一轮分配和收集过程中桶的管理开销。当d和k相对于n较小或固定时，基数排序非常高效。

空间复杂度:

空间复杂度主要来自于存储桶（或列表）的需要。基数排序需要额外的空间来存放每个基数下的元素。最坏情况下，每个元素都会进入不同的桶中，因此空间复杂度为O(n+k)。但实际上，由于基数排序是分轮进行的，每轮只需要足够的空间来存放每个桶中的元素，理想情况下空间复杂度可以近似为O(n)。但是，考虑到实际实现中可能会为每一轮都分配桶空间，总的空间复杂度还是O(n+k)。

稳定性:

基数排序是稳定的排序算法。这意味着相等的元素在排序前后相对位置保持不变。这是因为基数排序是按位进行的，每一趟排序都是独立的，并且在收集阶段按照原顺序从桶中取出元素，从而保持了稳定性。

桶排序:

初始化桶：首先确定桶的数量和每个桶覆盖的数值范围。桶的数量和分布取决于待排序数据的特性，通常需要预先知道数据的大致分布情况。
分配元素到桶：遍历待排序数组，根据元素的值将它们分配到对应的桶中。分配的依据可以是元素的大小，例如，如果数据范围是0到100，可以创建10个桶，每个桶负责10个数的范围。
桶内排序：对每个非空的桶内部进行排序。可以选择插入排序、快速排序等算法，具体选择取决于桶内元素的数量和特性。
合并桶：将所有桶中的元素按照桶的顺序（通常是桶的索引）依次取出，合并到一个数组中，这样合并后的数组就是有序的。

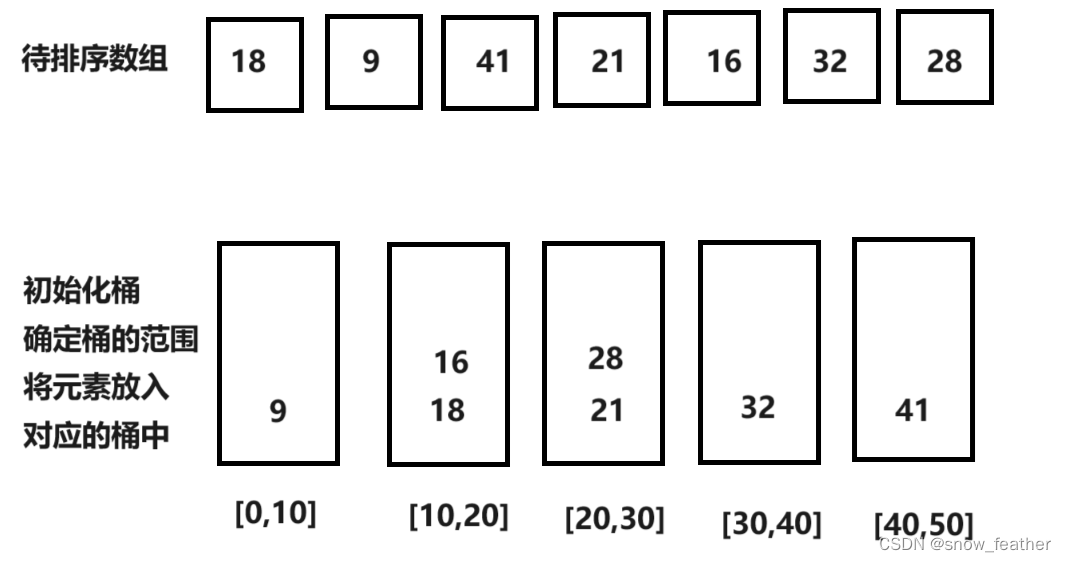
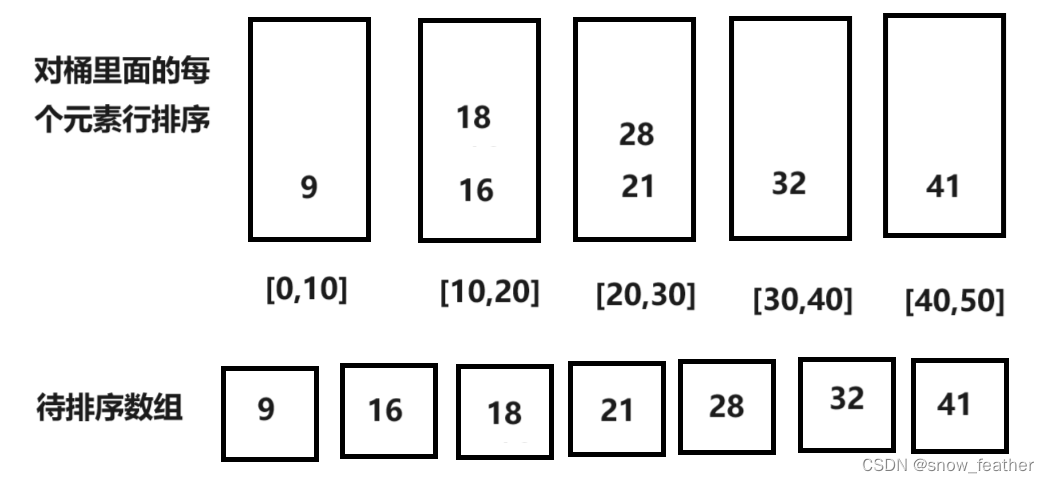
代码实现：

public static int[] bucketSort(int[] arr){

        int max = Integer.MIN_VALUE;
        int min = Integer.MAX_VALUE;
        for(int num : arr){
            max = Math.max(max,num);
            min = Math.min(min,num);
        }

        //初始化桶
        int bucketnum = (max-min)/arr.length+1;
        List<Integer>[] buckets = new ArrayList[bucketnum];
        for (int i = 0; i < bucketnum; i++) {
            buckets[i] = new ArrayList<>();
        }

        //将每个元素放入桶中
        for (int i = 0; i < arr.length; i++) {
            int index = (arr[i] - min) * (bucketnum - 1) / (max - min);
            buckets[index].add(arr[i]);
        }

        //对桶里面的每个元素进行排序，这里可以自己实现其他排序算法
        for (int i = 0; i < buckets.length; i++) {
            Collections.sort(buckets[i]);
        }

        //重新将桶中的每个元素放回到原数组中
        int index = 0;
        for (int i = 0; i < buckets.length; i++) {
            for(int j = 0;j<buckets[i].size();j++){
                arr[index] = buckets[i].get(j);
                index++;
            }
        }
        return arr;

    }

时间复杂度:

最好情况：如果数据均匀分布在各个桶中，且桶内排序所用的算法具有良好的时间复杂度（如插入排序在小数组上接近O(n)），桶排序的整体时间复杂度可以达到O(n + k)，其中n是待排序元素的数量，k是桶的数量。
平均情况：同样，如果数据分布较为均匀，桶排序的时间复杂度也是O(n + k)。
最坏情况：如果所有数据都集中在少数几个桶中，特别是全部集中在同一个桶里，此时桶排序的时间复杂度退化，需要对这些桶内的元素进行排序，可能会达到O(n^2)，这取决于桶内排序算法的时间复杂度。

空间复杂度: