87合并两个有序的数组

import java.util.*;
public class Solution {
public void merge(int A[], int m, int B[], int n) {
int i = m-1;
int j = n-1;
for(int k = n+m-1;k>=0;k--){
if(j<0) A[k] = A[i--];
else if(i<0) A[k] = B[j--];
else if(A[i]>B[j]) A[k] = A[i--];
else A[k] = B[j--];
}
}
}
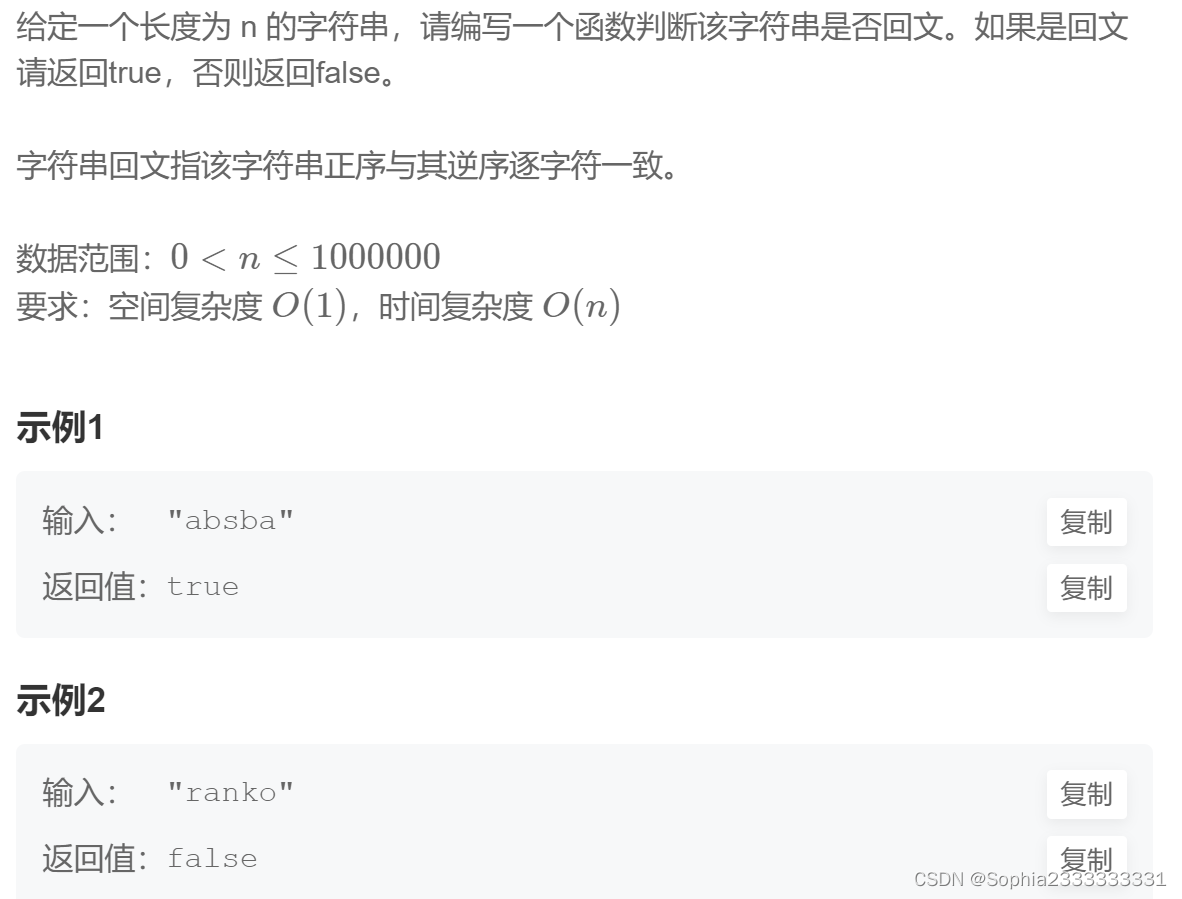
88 判断是否是回文串
import java.util.*;
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
* @param str string字符串 待判断的字符串
* @return bool布尔型
*/
public boolean judge (String str) {
// write code here
for(int i = 0,j=str.length()-1;i<=j;i++,j--){
if(str.charAt(i)!=str.charAt(j)) return false;
}
return true;
}
}
89 合并区间

import java.util.*;
/**
* Definition for an interval.
* public class Interval {
* int start;
* int end;
* Interval() { start = 0; end = 0; }
* Interval(int s, int e) { start = s; end = e; }
* }
*/
public class Solution {
public ArrayList<Interval> merge(ArrayList<Interval> intervals) {
ArrayList<Interval> res = new ArrayList<Interval>();
//按起点从小到大排序
Collections.sort(intervals,new Comparator<Interval>(){
@Override
public int compare(Interval o1,Interval o2){
return o1.start-o2.start;
}
});
if(intervals.size()<=1) return intervals;
Interval cur = intervals.get(0);
for(int i=1;i<intervals.size();i++){
Interval next = intervals.get(i);
if(next.start<=cur.end)
//区间有可能是完全被包含的
cur.end = Math.max(cur.end,next.end);
else{
res.add(cur);
cur = intervals.get(i);
}
}
//最后一个要add
res.add(cur);
return res;
}
}
排序时间O(Nlogn)空间复杂度O(1),res为返回必要空间,没有使用额外辅助空间
90 最小覆盖子串

滑动窗口
设置两个指针left,right。表示S的子串tmp可由left和right表示,当需要添加元素时候,就将right++,pop元素就left++。
我们用哈希表判断left到right是否完全包含T,动态维护窗口中所有字符以及个数。具体过程如下:
如果新加入的字符是被需要的(指在T里面),那么这个字符加入到窗口中,当窗口中的字符数目和被需要的数目相等时候,匹配度加一。right右移,这里匹配度是window里面的字符与need里面字符相等的数目。
如果新加入的字符不被需要(指不在T里面),right右移
当匹配度等于被需要的字符种类数,说明left-right覆盖到了T的所有字符,并且记录当前的left和right位置,然后就开始向右移动left
如果left位置的字符是被T所需要的,windo所统计的left字符要减一,当窗口中left处的字符数目小于need的字符数目,匹配度减一
如果left位置的字符不是被T所需要的,直接右移即可。
import java.util.*;
public class Solution {
/**
*
* @param S string字符串
* @param T string字符串
* @return string字符串
*/
public String minWindow (String S, String T) {
// write code here
//23
int n = T.length();
int match = 0;
//need的存放字符串T的所有字符统计
HashMap<Character,Integer> need = new HashMap<>();
//window 存放现有的窗口中出现在need中的字符统计
HashMap<Character,Integer> win = new HashMap<>();//窗口中已经出现的need
for(int i=0;i<T.length();i++){
if(need.containsKey(T.charAt(i))) need.compute(T.charAt(i),(key,value)->value+1);
else
need.put(T.charAt(i),1);
}
int left = 0;
int right = 0;
//表示窗口左右位置的指针
int start = 0;
//start 表示最后结果字符串开始位置
int minLen = Integer.MAX_VALUE;
//minlen表示最后字符串长度
while(right<S.length()){
char c = S.charAt(right);
if(need.containsKey(c)){
if(win.containsKey(c))
win.put(c,win.get(c)+1);
// win.compute(c,(key,value)->value+1);两种写法都行
else
win.put(c,1);
if(need.get(c)>=win.get(c)) match++;
}
right++;
while(match==n){
//当匹配度等于need.size(),说明这段区间可以作为候选结果,左指针右移
if(right-left<minLen){
minLen = right-left;
start = left;
}
char c2 = S.charAt(left);
if(need.containsKey(c2)){
if(win.get(c2)>1) win.compute(c2,(key,value)->value-1);
else
win.remove(c2);
if(!win.containsKey(c2)||need.get(c2)>win.get(c2)) match--;
}
left++;
}
}
return minLen == Integer.MAX_VALUE?"":S.substring(start,start+minLen);
}
}
字符串仅包含大小写字母,则字符集是已知且有限的,那这种情况下我们可以考虑快速查找某个元素是否出现过的哈希表——只需要维护一个哈希表,将字符串T中的字符作为key值,初始化时当字符在T中出现一次则对应的value值减1:
更简洁一些:
import java.util.*;
public class Solution {
/**
*
* @param S string字符串
* @param T string字符串
* @return string字符串
*/
public boolean isAll(int[] hash){
//判断所有都不为负才说明包含了所有T
for(int i=0;i<hash.length;i++){
if(hash[i]<0) return false;
}
return true;
}
public String minWindow (String S, String T) {
// write code here
//A-Z 65-90
//a-z 97-122 60大小就够了
int[] hash = new int[60];//存出现过的字母出现的次数,T需要的先-1一次,其他为0
Arrays.fill(hash,0);
for(int i=0;i<T.length();i++){
hash[T.charAt(i)-'A'] -= 1;//以后遇上再加
}
int left = 0;
int right = 0;
int minLen = Integer.MAX_VALUE;
int start = 0;//最后结果的位置的start
while(right<S.length()){
hash[S.charAt(right)-'A']++;
right++;
//包含了所有的T
while(isAll(hash)){
if(right-left<minLen){
minLen = right-left;
start = left;
}
hash[S.charAt(left)-'A']--;
left++;
}
}
return minLen == Integer.MAX_VALUE?"":S.substring(start,start+minLen);
}
}
92 最长无重复子数组

用双指针/滑动窗口,用set判断只要没出现过就右指针右移,出现重复就记录长度,然后左指针右移
import java.util.*;
public class Solution {
/**
*
* @param arr int整型一维数组 the array
* @return int整型
*/
public int maxLength (int[] arr) {
// write code here
int max = Integer.MIN_VALUE;
int left = 0;
int right = 0;
HashSet<Integer> set = new HashSet<>();
while(right<arr.length){
if(!set.contains(arr[right])){
//没重复就右指针右移
set.add(arr[right]);
right++;
}else{
//遇到重复的就记录,左指针右移
max = Math.max(max,right-left);
set.remove(arr[left]);
left++;
}
}
return max==Integer.MIN_VALUE?arr.length:max;
}
}
HashSet中的contains在O(1)(恒定时间)中执行,所以整体的时间复杂度还是O(n)
93 盛水最多的容器

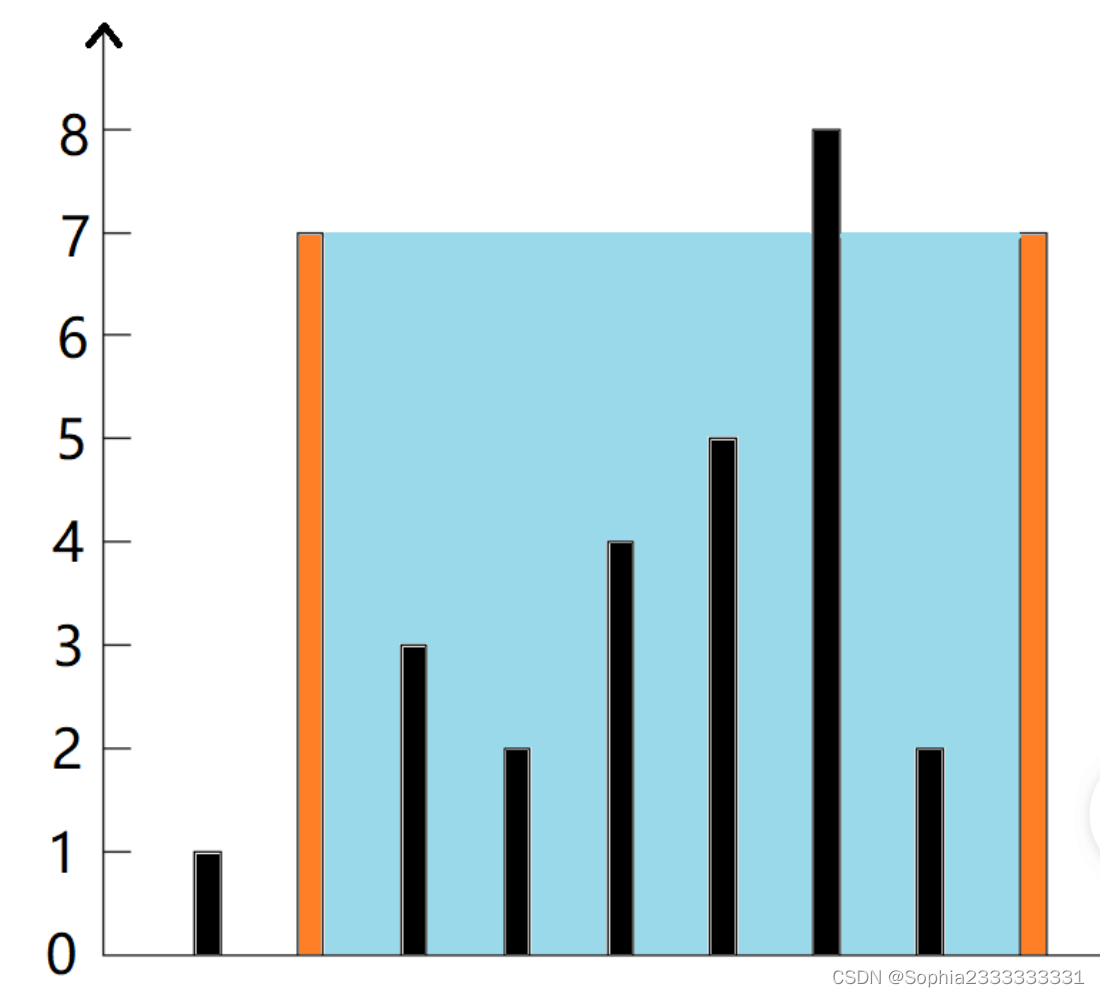

可以利用贪心思想:我们都知道容积与最短边长和底边长有关,与长的底边一定以首尾为边,但是首尾不一定够高,中间可能会出现更高但是底边更短的情况,因此我们可以使用对撞双指针向中间靠,这样底边长会缩短,因此还想要有更大容积只能是增加最短变长,此时我们每次指针移动就移动较短的一边,因为贪心思想下较长的一边比较短的一边更可能出现更大容积。
每次移动较短的那个指针,从两边往中间移动
import java.util.*;
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param height int整型一维数组
* @return int整型
*/
public int maxArea (int[] height) {
// write code here
//20
if(height.length<2) return 0;
int left = 0;
int right = height.length-1;
int max = -1;
while(left<right){
max = Math.max(max,Math.min(height[left],height[right])*(right-left));
//移动较短的一边
if(height[left]<height[right]) left++;
else right--;
}
return max;
}
}
step 1:优先排除不能形成容器的特殊情况。
step 2:初始化双指针指向数组首尾,每次利用上述公式计算当前的容积,维护一个最大容积作为返回值。
step 3:对撞双指针向中间靠,但是依据贪心思想,每次指向较短边的指针向中间靠,另一指针不变。
时间复杂度:O(n),双指针共同遍历一次数组
空间复杂度:O(1),常数级变量,没有额外辅助空间
94 接雨水问题
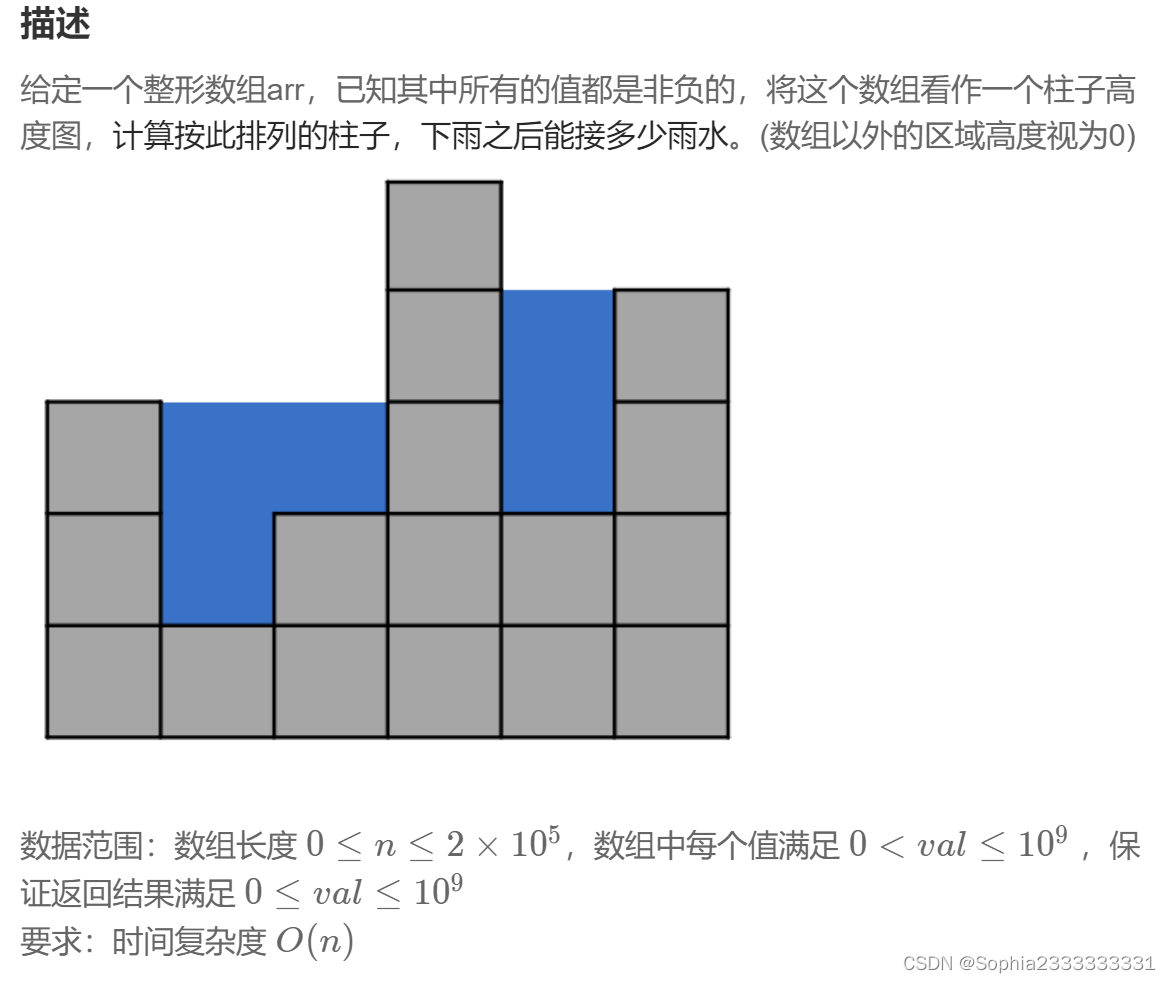
将整个图看成一个水桶,两边就是水桶的板,中间比较低的部分就是水桶的底,由较短的边控制水桶的最高水量。但是水桶中可能出现更高的边,比如上图第四列,它比水桶边还要高,那这种情况下它是不是将一个水桶分割成了两个水桶,而中间的那条边就是两个水桶的边。
有了这个思想,解决这道题就容易了,因为我们这里的水桶有两个边,因此可以考虑使用对撞双指针往中间靠。
具体做法:
step 1:检查数组是否为空的特殊情况
step 2:准备双指针,分别指向数组首尾元素,代表最初的两个边界
step 3:指针往中间遍历,遇到更低柱子就是底,用较短的边界减去底就是这一列的接水量,遇到更高的柱子就是新的边界,更新边界大小。
import java.util.*;
public class Solution {
/**
* max water
* @param arr int整型一维数组 the array
* @return long长整型
*/
public long maxWater (int[] arr) {
// write code here
int res = 0;
int left = 0;
int right = arr.length-1;
if(arr.length<3) return 0;
int height = Math.min(arr[left],arr[right]);
while(left<right){
//每次都要更新
if(arr[left]<arr[right]){
left++;
res += Math.max(height-arr[left],0);
//取第二大的是更新后的height
//height是左右较小的那个height<arr[right],现在新出现的是arr[left]
if(height<arr[left]&&arr[left]<arr[right]) height = arr[left];
else if(arr[left]>=arr[right]) height = arr[right];
}else{
right--;
res+= Math.max(height-arr[right],0);
//height是左右较小的那个height<arr[left],现在新出现的是arr[right]
if(height<arr[right]&&arr[right]<arr[left]) height = arr[right];
else if(arr[right]>=arr[left]) height = arr [left];
}
}
return res;
}
}
height就是左右和新出现的边三者中第二大的,关于height的更新debug了很久
题解的写法更简洁一些,只是看题的时候不容易想到:用双指针从两边往中间,同时存左右两边出现过的最大值,二者较小的就是高
import java.util.*;
public class Solution {
public long maxWater (int[] arr) {
//排除空数组
if(arr.length == 0)
return 0;
long res = 0;
//左右双指针
int left = 0;
int right = arr.length - 1;
//中间区域的边界高度
int maxL = 0;
int maxR = 0;
//直到左右指针相遇
while(left < right){
//每次维护往中间的最大边界
maxL = Math.max(maxL, arr[left]);
maxR = Math.max(maxR, arr[right]);
//较短的边界确定该格子的水量
if(maxR > maxL)
res += maxL - arr[left++];
else
res += maxR - arr[right--];
}
return res;
}
}