64. 最小路径和

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例 1：

输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

示例 2：

输入：grid = [[1,2,3],[4,5,6]]
输出：12

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 200
• 0 <= grid[i][j] <= 200

class Solution {
    public int minPathSum(int[][] grid) {
        int dp[][]=new int [grid.length][grid[0].length];
        int sum=0;
        for (int i = 0; i < grid[0].length; i++) {
            sum+=grid[0][i];
            dp[0][i]=sum;
        }
        sum=0;
        for (int i = 0; i < grid.length; i++) {
            sum+=grid[i][0];
            dp[i][0]=sum;
        }
        for (int i = 1; i < grid.length; i++) {
            for (int j = 1; j < grid[0].length; j++) {
                dp[i][j]=Math.min(dp[i-1][j]+grid[i][j],dp[i][j-1]+grid[i][j]);
            }
        }
        return dp[grid.length-1][grid[0].length-1];
    }
}

53. 最大子数组和

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组

是数组中的一个连续部分。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

示例 2：

输入：nums = [1]
输出：1

示例 3：

输入：nums = [5,4,-1,7,8]
输出：23

提示：

• 1 <= nums.length <= 105
• -104 <= nums[i] <= 104

以下是错误示范

//这个超出内存限制。。。

class Solution {
    public int maxSubArray(int[] nums) {
        int max=nums[0];
        int dp[][]=new int [nums.length][nums.length];
        for (int i = 0; i < dp.length; i++) {
            dp[i][i]=nums[i];
            max=Math.max(dp[i][i],max);
        }
        for (int i = 1; i < nums.length; i++) {
            for (int j = 0; j < i; j++) {
                dp[i][j]=dp[i-1][j]+nums[i];
                max=Math.max(dp[i][j],max);
            }
        }
        return max;
    }
}

//以为是定义了二维数组dp[][]占内存太大
//改了之后超时。。。

class Solution {
    public int maxSubArray(int[] nums) {
        int max=nums[0];
        for (int t = 0; t < nums.length; t++) {
            int sum=0;
            for (int i = t; i < nums.length; i++) {
                sum+=nums[i];
                max=Math.max(sum,max);
            }
        }
        return max;
    }
}

62. 不同路径

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

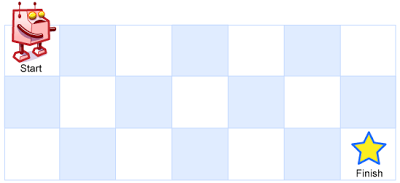
输入：m = 3, n = 7
输出：28

示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

示例 3：

输入：m = 7, n = 3
输出：28

示例 4：

输入：m = 3, n = 3
输出：6

提示：

• 1 <= m, n <= 100
• 题目数据保证答案小于等于 2 * 109

class Solution {
    public int uniquePaths(int m, int n) {
        int[][] dp=new int[m][n];
        for (int i = 0; i < m; i++) {
            dp[i][0]=1;
        }
        for (int i = 1; i < n; i++) {
            dp[0][i]=1;
        }
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j]=dp[i-1][j]+dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
}