十种常见排序算法可以分类两大类别：比较类排序和非比较类排序。      

  

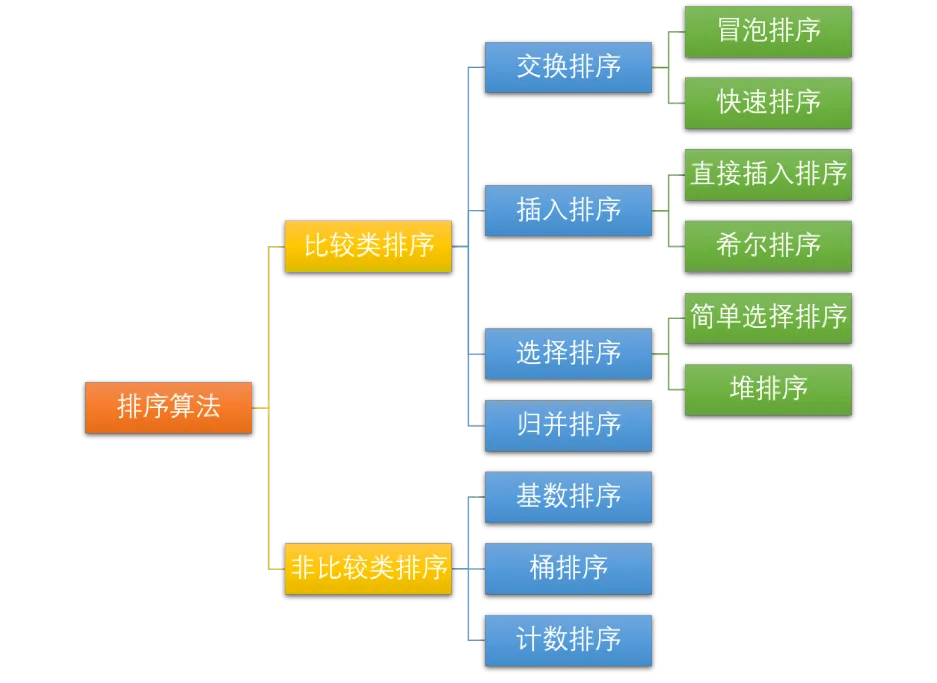
        常见的快速排序、归并排序、堆排序以及冒泡排序等都属于比较类排序算法。比较类排序是通过比较来决定元素间的相对次序，其时间复杂度不能突破 O(nlogn)。在冒泡排序之类的排序中，问题规模为 n，又因为需要比较 n 次，所以平均时间复杂度为 O(n²)。在归并排序、快速排序之类的排序中，问题规模通过分治法消减为 logn 次，所以时间复杂度平均 O(nlogn)。

        非比较类排序不通过比较来决定元素间的相对次序，而是通过确定每个元素之前，应该有多少个元素来排序。非比较排序时间复杂度底，但由于非比较排序需要占用空间来确定唯一位置。所以对数据规模和数据分布有一定的要求。

1、冒泡排序

        冒泡排序是一种简单的排序算法。它重复地遍历要排序的序列，依次比较两个元素，如果它们的顺序错误就把它们交换过来。遍历序列的工作是重复地进行直到没有再需要交换为止，此时说明该序列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢 “浮”到数列的顶端。

实现代码：

/**
 * 冒泡排序
 * @param arr
 * @return arr
 */
public static int[] bubbleSort(int[] arr) {
    for (int i = 1; i < arr.length; i++) {
        boolean flag = true;
        for (int j = 0; j < arr.length - i; j++) {
            if (arr[j] > arr[j + 1]) {
                int tmp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = tmp;
                
                flag = false;
            }
        }
        if (flag) {
            break;
        }
    }
    return arr;
}

         此处对代码做了一个小优化，加入了一个Flag变量，当原输入序列就是排序好的情况下，停止遍历，此时时间复杂度为O(n)。

算法分析：

• 稳定性：稳定
• 时间复杂度：最佳：O(n) , 最差：O(n2)，平均：O(n2)
• 空间复杂度：O(1)

2、选择排序

        选择排序的思想更加朴实：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。其时间复杂度永远都是O(n2)。

实现代码：

/**
 * 选择排序
 * @param arr
 * @return arr
 */
public static int[] selectionSort(int[] arr) {
    for (int i = 0; i < arr.length - 1; i++) {
        int minIndex = i;
        for (int j = i + 1; j < arr.length; j++) {
            if (arr[j] < arr[minIndex]) {
                minIndex = j;
            }
        }
        if (minIndex != i) {
            int tmp = arr[i];
            arr[i] = arr[minIndex];
            arr[minIndex] = tmp;
        }
    }
    return arr;
}

• 稳定性：不稳定
• 时间复杂度：最佳：O(n2) , 最差：O(n2)，平均：O(n2)
• 空间复杂度：O(1)

3、快速排序

        快速排序的基本思想：通过一趟排序将待排序列分隔成独立的两部分，其中一部分记录的元素均比另一部分的元素小，则可分别对这两部分子序列继续进行排序，以达到整个序列有序。

算法步骤：

• 从序列中随机挑出一个元素，做为 “基准”(pivot)；
• 重新排列序列，将所有比基准值小的元素摆放在基准前面，所有比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个操作结束之后，该基准就处于数列的中间位置。
• 递归地把小于基准值元素的子序列和大于基准值元素的子序列进行快速排序。

实现代码：

public static void quick_sort(int nums[], int start, int end){
        if(start >= end) return;
        int left = start;
        int right = end;
        int base = nums[start];
        while(left < right){
            while(left < right && nums[right] >= base){
                right--;
            }
            nums[left] = nums[right];
            while(left < right && nums[left] <= base){
                left++;
            }
            nums[right] = nums[left];
        }
        //此时left = right
        nums[left] = base;
        quick_sort(nums,start,left-1);
        quick_sort(nums,left+1,end);
    }

• 稳定性：不稳定
• 时间复杂度：最佳：O(nlogn) , 最差：O(nlogn)，平均：O(nlogn)
• 空间复杂度：O(logn)

4、堆排序

        堆排序(Heap Sort)是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于(或者大于)它的父节点。堆的底层是一棵完全二叉树。而完全二叉树是一层一层按照进入的顺序排成的。按照这个特性，我们可以用数组来按照完全二叉树实现堆。

算法步骤：

1. 构建初始堆，将待排序列构成一个大顶堆(或者小顶堆)，升序大顶堆，降序小顶堆；
2. 将堆顶元素与堆尾元素交换，并断开(从待排序列中移除)堆尾元素。
3. 重新构建堆。
4. 重复2~3，直到待排序列中只剩下一个元素(堆顶元素)。

代码实例：

import java.util.Arrays;

/**
 * @description: 手撕堆排序
 * @author: Jay
 * @create: 2024-05-02 11:48
 **/
public class heapSort {
    //堆的长度大小
    static int heapLen;
    //定义 交换数组两元素 的函数
    private static void swap(int[] arr, int a, int b){
        int temp = arr[a];
        arr[a] = arr[b];
        arr[b] = temp;
    }
    //初始化构建大顶堆
    private static void buildHeap(int[] arr){
        //从最后一个非叶子节点开始,对应的索引为 arr.length / 2 - 1
        for(int i=arr.length/2-1; i>=0; i--){
            adjustHeap(arr,i);
        }
    }
    //调整堆
    private static void adjustHeap(int[] arr, int i){
        int left = i * 2 + 1;
        int right = i * 2 + 2;
        int largest = i;
        if(right < heapLen && arr[right] > arr[largest]){
            largest = right;
        }
        if(left < heapLen && arr[left] > arr[largest]){
            largest = left;
        }
        if(largest != i){
            swap(arr,largest,i);
            adjustHeap(arr,largest); //交换之后，子节点可能不满足堆的性质了，需要重新调整。
        }
    }
    //测试
    public static void main(String[] args) {
        int[] arr = {16,7,3,20,17,8};
        heapLen = arr.length;
        buildHeap(arr);
        //交换堆顶和堆尾元素，再重新调整堆。
        for(int i=arr.length-1; i>0; i--){
            swap(arr,i,0);
            heapLen--;
            adjustHeap(arr,0);
        }
        System.out.println(Arrays.toString(arr));
    }
}