问题描述
农民约翰的 N头奶牛(编号为 1…N)计划逃跑并加入马戏团,为此它们决定练习表演杂技。
奶牛们不是非常有创意,只提出了一个杂技表演:
叠罗汉,表演时,奶牛们站在彼此的身上,形成一个高高的垂直堆叠。
奶牛们正在试图找到自己在这个堆叠中应该所处的位置顺序。
这 N头奶牛中的每一头都有着自己的重量 Wi以及自己的强壮程度 Si。
一头牛支撑不住的可能性取决于它头上所有牛的总重量(不包括它自己)减去它的身体强壮程度的值,现在称该数值为风险值,风险值越大,这只牛撑不住的可能性越高。
您的任务是确定奶牛的排序,使得所有奶牛的风险值中的最大值尽可能的小。
输入格式
第一行输入整数 N,表示奶牛数量。
接下来 N行,每行输入两个整数,表示牛的重量和强壮程度,第 i行表示第 i头牛的重量 Wi以及它的强壮程度 Si。
输出格式
输出一个整数,表示最大风险值的最小可能值。
数据范围
1≤N≤50000,1≤Wi≤10,000,1≤Si≤1,000,000,000
输入样例
3
10 3
2 5
3 3
输出样例
2
问题分析
通过题目,我们知道每头牛的危险值=它上面牛的重量之和-自身的强壮值。
要使每头牛的危险值最小,根据贪心思想:
- 自身w值越大应该放到底部(即减小上面式子中的被减数)
- 自身s值越大应该放到底部(即增大上述中的减数);
所以每头牛的(w+s)值越大应该排在后面,即升序排序。
数学分析证明:

交换之前其他牛的危险值不变
- i之前的牛并不涉及牛i与i+1的重量值。
- i+1之后的牛只涉及到牛i与i+1重量值的和
所以交换分析前后这两头牛中最大的危险值即可。
将上述式子进行化简,得到下面的式子
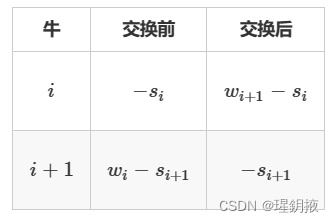
由于s,w都是整数,wi-si+1>-si+1,wi+1-si>-si;比较wi-si+1,wi+1-si即可
- 当wi-si+1>=wi+1-si,即wi+si>=wi+1+si+1时,交换后更优
- 当wi-si+1<wi+1-si,即wi+si<wi+1+si+1时,交换前更优
所以得到做法:按每头牛的w+s进行排序。
然后根据题意算出每头牛的危险值记录其中的最大值即可。
代码
#include<bits/stdc++.h>
using namespace std;
const int N=50010;
typedef pair<int,int> PII;
PII cow[N]; // 定义一个pair类型的数组,用于存储牛的重量和能力值
int n; // 牛的数量
int main()
{
cin>>n; // 输入牛的数量
for(int i=0;i<n;i++)
{
int w,s; // w表示牛的重量,s表示牛的能力值
cin>>w>>s; // 输入每头牛的重量和能力值
cow[i]={w+s,w}; // 将每头牛的重量和能力值存入数组中
}
sort(cow,cow+n); // 对数组进行排序,按照重量和能力值的和从小到大排序
int res=-2e9,sum=0; // res表示结果,sum表示当前牛的总重量
for(int i=0;i<n;i++)
{
int s=cow[i].first-cow[i].second,w=cow[i].second; // 计算当前牛的能力值和重量
res=max(res,sum-s); // 更新结果
sum+=w; // 更新总重量
}
cout<<res<<endl; // 输出结果
return 0;
}