【算法与数据结构】哈希表

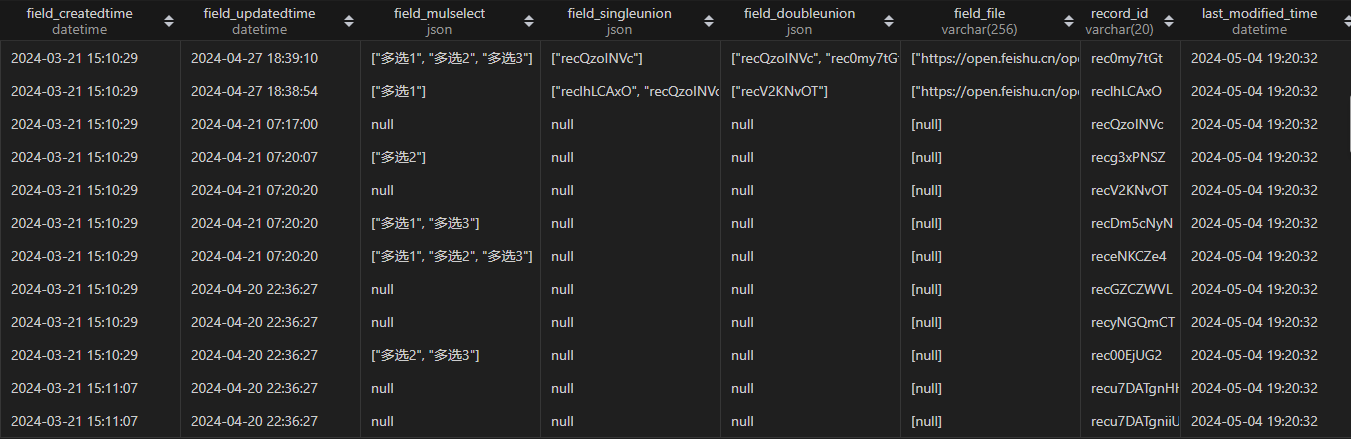
文章目录

- 引入
- 哈希函数
- - 介绍
  - 便利店的例子
  - Python3 中的哈希表
  - C++ 中的哈希表
- 应用
- - 将散列表用于查找
  - 防止重复
  - 将散列表用作缓存
- 哈希冲突与解决
- - 链地址法
  - 开放寻址
- 总结
- 参考资料
- 写在最后

引入

假设你在一家便利店上班，你不熟悉每种商品的价格，在顾客需要买单是时候，你需要在价目表中一个个找出商品的价格，这需要很长的时间，按照现行搜索的方式，需要花费 $O (n)$ 的时间，如果本子中的商品是按照顺序排列的，使用二分法就可以找出某件商品的价格，这时的时间复杂度为 $O (l o g n)$ 。

那有没有一种可以更快的找出某样商品价格的方法呢？有，利用哈希表查找，可以将时间复杂度降到 $O (1)$ 。

在数组这种数据结构中，可以通过索引 $O (1)$ 的找到指定索引对应的元素值。一行行的查找商品的价格就是在数组中一个个枚举，这个数组中包含两个元素：商品名和价格。如果将这个数组按照商品名排序，就可以使用二分查找在其中查找商品的价格，时间复杂度为 $O (l o g n)$ 。如果用一个函数，输入商品名，输出对应在数组中的位置（索引），那么我们可以直接利用索引 $O (1)$ 的查找到商品的价格。

这个函数被称为 哈希函数，也有的资料称之为 散列函数。

哈希函数

介绍

哈希函数，你给它输入任何类型的数据，它都会输出一个数字。用专业的术语来说就是 “将输入映射到数字“。哈希函数具有一些要求：

相同的输入映射到相同的数字。例如，你输入苹果到哈希函数时得到 4，你再次输入苹果时，还是会得到 4.
不同的输入映射到不同的数字。例如，你输入苹果到哈希函数时得到 4，当你输入不同的水果到哈希函数会得到不同于 4 的数字，可能是 5、6 等等数字。

便利店的例子

哈希函数将输入映射到数字，这有何用途？以便利店的例子为例，你可以通过哈希函数建立商品与价格查询表，方便快速查询商品的对应价格。

首先创建一个空数组，用来存放商品的价格。

下面将苹果的价格加入到数组中，为此，需要将 “apple” 作为输入交给哈希函数，这时哈希函数输出 3，因此我们将苹果的价格存储到数组索引 3 位置处。

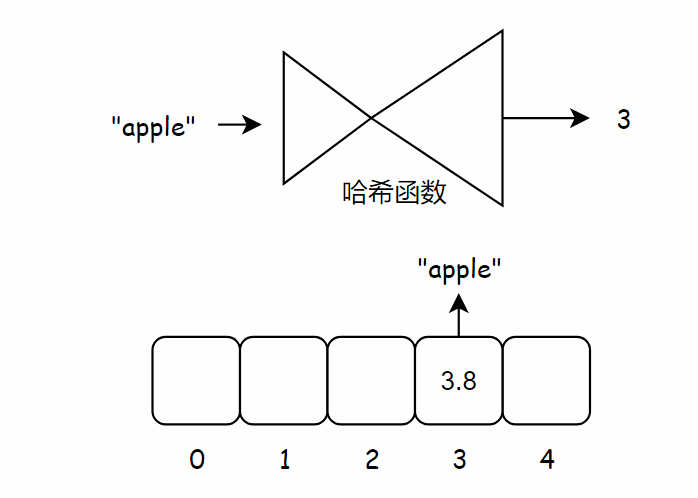
下面将香蕉的价格加入到数组中，为此，需要将 “banana” 作为输入交给哈希函数，这时哈希函数输出 0，因此我们将香蕉的价格存储到数组索引 0 位置处。

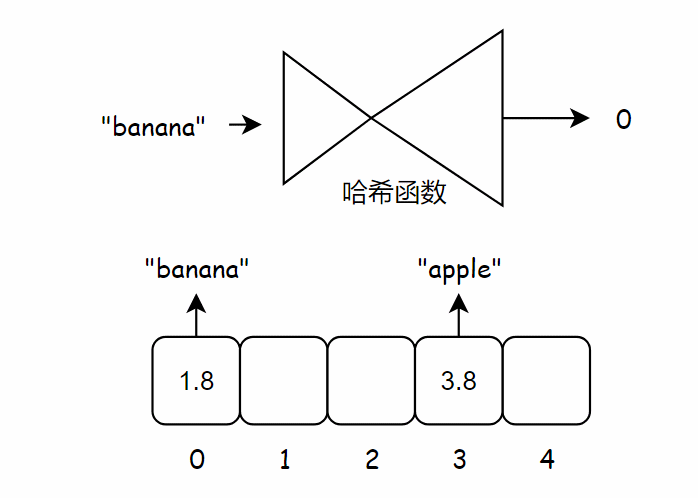
不断重复这个过程，最终整个数组将被价格填满。

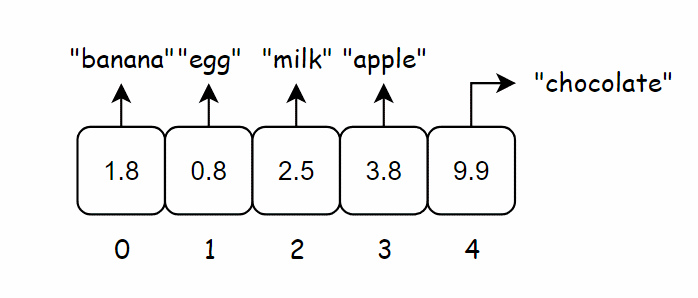
现在假设需要找到 “chocolate” 的价格，你无需在数组中查找，只需要将 “chocolate” 输入到哈希函数。

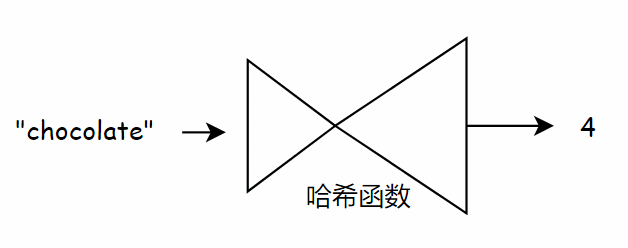
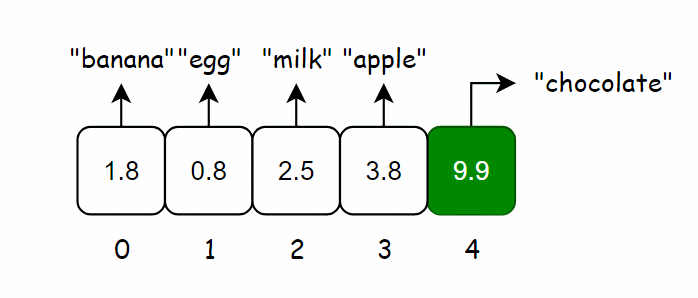
哈希函数会告诉你 “chocolate” 存储在索引 4 处，于是直接对数组进行索引得到 “chocolate” 的价格。

Python3 中的哈希表

在平时的使用中，我们不需要自己去实现哈希表，任何一种优秀的程序语言都提供了哈希表的实现。在 Python3 中提供的哈希表为字典，你可以使用函数 dict 创建哈希表。字典中的元素是一个个的对，对的一个元素是键，第二个元素是键对应的值。

比如上述便利店的例子，可以直接使用字典建立商品名到价格的映射。

book = dict()

book["apple"] = 3.8
book["banana"] = 1.8
book["egg"] = 0.8
book["milk"] = 2.5
book["chololate"] = 9.9

print(book["chololate"]) # 直接输出 "chololate" 的价格

C++ 中的哈希表

C++ 中提供的哈希表是 map 和 unordered_map，前者按照键进行排序的有序哈希表，后者则是无序哈希表。常用操作有：

增加
查询
删除

以上述便利店的例子对以上两个常用操作进行简要说明：

unordered_map<string, double> book;

// 在哈希表中增加键值对
book["apple"] = 3.8;
book["banana"] = 1.8;
book["egg"] = 0.8;
book["milk"] = 2.5;
book["chololate"] = 9.9;

// 查询指定键对应的值
double price = book["chololate"];

// 删除键值对
book.erase("chololate")

应用

哈希表通常有以下几方面的应用：

将散列表用于查找
防止重复
将散列表用作缓存

将散列表用于查找

第一点在上述便利店的例子中已经解释过了，这里不再赘述。

防止重复

第二点应用实际是利用哈希集合，本质上也是使用哈希函数将输入映射成唯一的数字，你可以理解成哈希函数输出的索引对应数组中的值为 1 或 0。如果某个元素存在于哈希集合中，那么索引对应的值为 1，否则为 0。

举一个具体的例子，你管理一个投票站，没人只允许投一票，为了避免重复投票，有人来投票时，你会询问他的名字，并将其与已投票名单进行比对：

如果名字在名单中，则不允许他再次投票；
否则允许他投票，并将其名字记录在已投票名单中。

利用哈希表或者哈希集合都可以在 $O (1)$ 时间复杂度内判断出某人是否已经投过票了。可以对比看一下分别哈希表和哈希集合的代码：

/*****使用哈希表*****/ 
unordered_map<string, int> voted;

// 增加已经投票的人
voted["Jim"] = 1;
voted["Pam"] = 1;

// 查询 Jim 是否已经投过票了，如果已经投过票返回 true，否则返回 false
if (voted.find(Jim) != voted.end()) {
	return true
}
else {
	return false;
}

/*****使用哈希集合*****/
unordered_set<string> voted;

// 增加已经投票的人
voted.insert("Jim");
voted.insert("Pam");

// 查询 Jim 是否已经投过票了，如果已经投过票返回 true，否则返回 false
if (voted.find(Jim) != voted.end()) {
	return true
}
else {
	return false;
}

将散列表用作缓存

通常我们访问一个网页链接，首先会在缓存中查找是否有这个链接，如果有直接从缓存中返回链接对应的内容；如果没有才会向相应的服务器发送请求，服务器做一些处理，生成一个我们需要的网页。

这种应用实际上将网页链接记作键，链接对应的内容作为键的值，这是哈希表的一个典型的应用场景。

哈希冲突与解决

通常情况下哈希函数的输入空间远大于输出空间，这就不可避免的会造成「冲突」，即多个元素映射到同一个数值上。这种冲突也被称为哈希冲突，会导致查询结果错误。

既然这个导致冲突的原因在于输出空间不够，我们直接「扩容」就好了。这种简单、有效，但是效率太低，因为哈希表扩容需要进行大量的数据移动和哈希值的重新计算。为了提升效率，通常采用以下策略：

改良哈希表的结构，使得哈希表在出现哈希冲突时仍可以正常使用
在必要的时候（哈希冲突比较严重时），进行扩容

哈希表的结构改良主要包括：

链地址法
开放寻址法

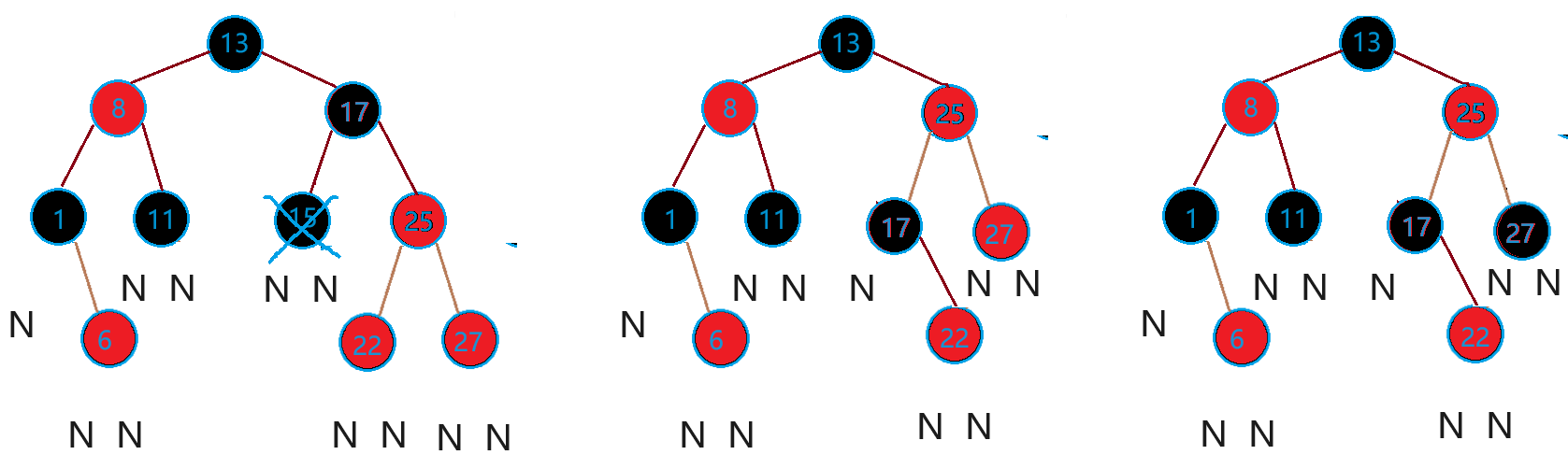
链地址法

在原始的哈希表中，每一个哈希值都对应数组中的一个索引，每一个索引对应的是数组中的一个位置。链地址法中每一个索引对应的是一条链表，具有相同哈希值的元素会被放入这一链表中。如下图。

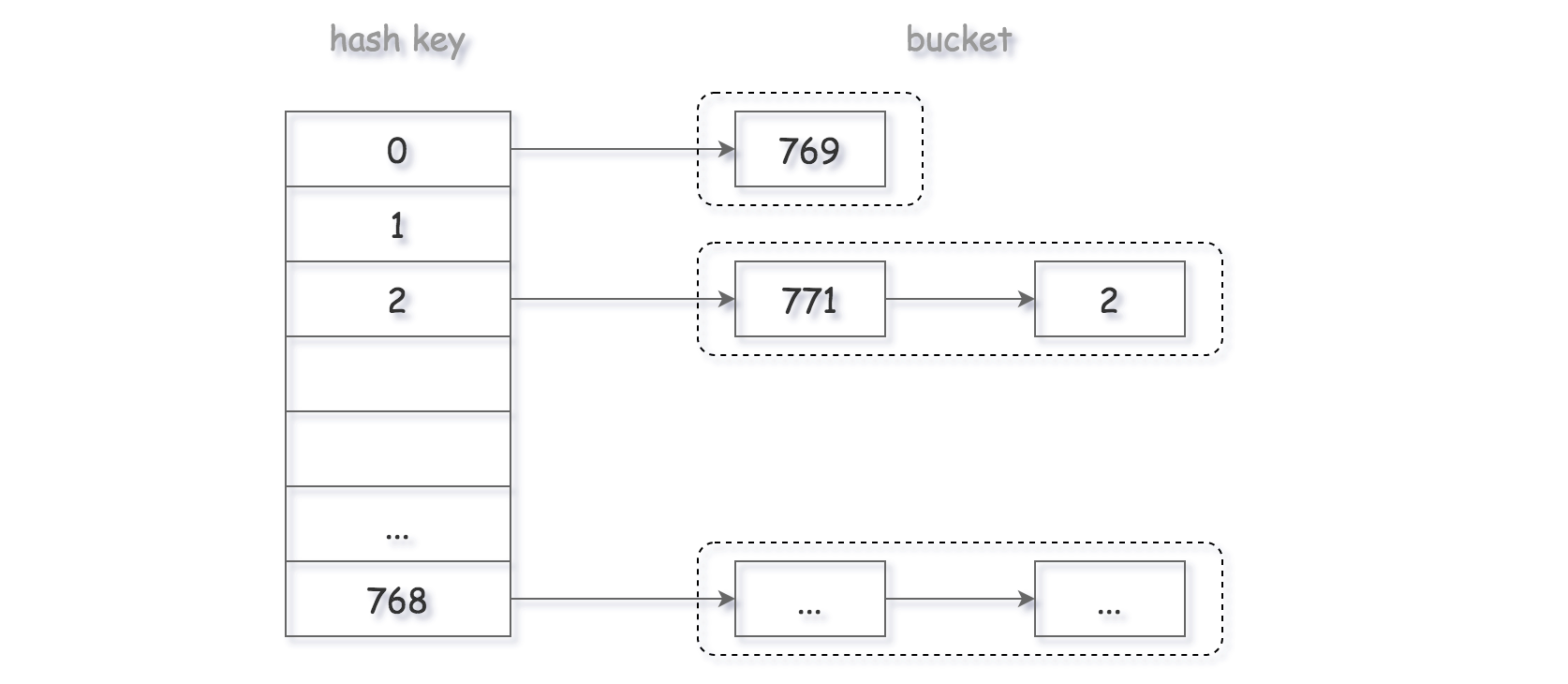
基于链式地址实现的哈希表的常用操作如下：

查找元素：输入 key 经过哈希函数得到索引，即可访问链表的头节点，然后遍历链表并对比 key 以查找目标键值对。
增加元素：通过哈希函数访问到对应的链表头节点，然后将节点添加到链表中。
删除元素：通过哈希函数访问到对应链表头部，遍历链表找到目标节点并删除该节点。

以下是一个链地址法的示例代码。已经在 706. 设计哈希映射中测试过。

class MyHashMap {
private:
    int size;           // 键值对数量
    int capacity;       // 哈希表容量
    double loadThres;   // 负载因子阈值
    int extendRatio;    // 扩容倍数
    vector<list<pair<int, int>>> data;

    // hash 函数
    int hash(int key) {
        return key % capacity;
    }

    // 计算负载因子
    double loadFactor() {
        return double(size) / double(capacity);
    }

public:
    // 构造函数
    MyHashMap(): size(0), capacity(8), loadThres(0.7), extendRatio(2), data(capacity) {}

    // 析构函数
    ~MyHashMap() {}

    // 添加键值对，若存在则更改键对应的值
    void put(int key, int val) {
        ++size;
        if (loadFactor() > loadThres) {
            extend();
        }
        int h = hash(key);
        for (auto it = data[h].begin(); it != data[h].end(); ++it) {
            if ((*it).first == key) {
                (*it).second = val;
                return;
            }
        }
        data[h].push_back(make_pair(key, val));
    }

    // 查找
    int get(int key) {
        int h = hash(key);
        for (auto it = data[h].begin(); it != data[h].end(); ++it) {
            if ((*it).first == key) {
                return (*it).second;
            }
        }
        return -1;
    }

    // 删除
    void remove(int key) {
        int h = hash(key);
        for (auto it = data[h].begin(); it != data[h].end(); ++it) {
            if ((*it).first == key) {
                data[h].erase(it);
                --size;
                return;
            }
        }
    }

    // 扩容
    void extend() {
        vector<list<pair<int, int>>> dataTmp = data;
        capacity *= extendRatio;
        data.clear();
        data.resize(capacity);
        size = 0;
        for (auto& ele : dataTmp) {
            for (auto it = ele.begin(); it != ele.end(); ++it) {
                put((*it).first, (*it).second);
            }
        }
    }
};