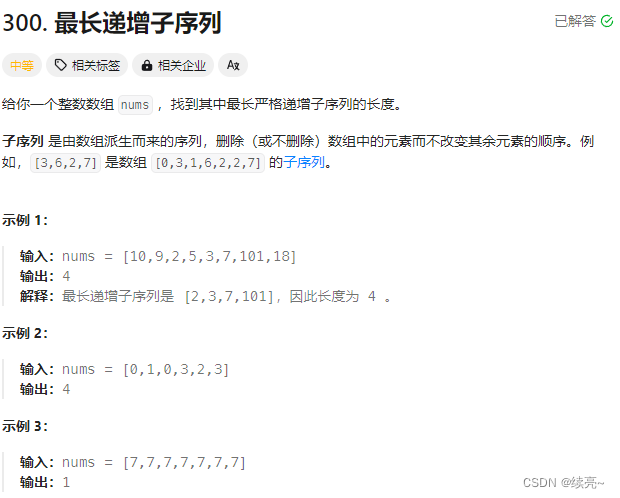
思路：

使用递归来理解题目，然后在看如何优化，假设我当前使用元素那么最长是多少，如果不使用当前元素最长是多少，然后取最大值。

代码如下：

//算出最长递增子序列的长度
    public static int lengthOfLIS02(int[] nums) {
        if (nums==null||nums.length==0){
            return 0;
        }
        if (nums.length==1){
            return 1;
        }
        return process(nums,0,-1,0,nums.length);
    }

    //从index...到N 最长的递增子序列是多长
    public static int process(int[] arr,int index,int preIndex,int curLen,int N){
      if (index==N){
          return curLen;
      }
      //当前index不要
      int p1=process(arr,index+1,preIndex,curLen,N);
      int p2=0;
      //当前index 要
      if (preIndex == -1 || arr[index] > arr[preIndex]){
          p2=process(arr,index+1,index,curLen+1,N);
      }
      return Math.max(p1,p2);
    }

改成动态规划：其中dp[i]表示以nums[i]结尾的最长子序列是多少

class Solution {
    /**
     * 计算数组 nums 的最长递增子序列的长度。
     * 使用动态规划，时间复杂度 O(n^2)。
     *
     * @param nums 输入的整数数组
     * @return 返回最长递增子序列的长度
     */
    public static int lengthOfLIS(int[] nums) {
        // 如果输入数组为空或长度为0，直接返回0
        if (nums == null || nums.length == 0) {
            return 0;
        }

        // 创建dp数组，dp[i]表示以nums[i]结尾的最长递增子序列的长度
        int[] dp = new int[nums.length];
        // maxLen用于记录并更新全局的最长递增子序列的长度
        int maxLen = 0;

        // 从后向前遍历数组，以保证每次计算dp[i]时，dp[j] (j > i)都已经被计算
        for (int i = nums.length - 1; i >= 0; i--) {
            dp[i] = 1;  // 初始化dp[i]为1，因为最短的子序列至少包含自身
            // 内层循环用于比较nums[i]和其后面的所有元素nums[j]
            for (int j = i + 1; j < nums.length; j++) {
                // 如果nums[j]大于nums[i]，则可以将nums[i]添加到以nums[j]结尾的递增子序列中
                if (nums[j] > nums[i]) {
                    dp[i] = Math.max(dp[i], dp[j] + 1); // 更新dp[i]为最大值
                }
            }
            // 更新全局最长递增子序列的长度
            maxLen = Math.max(maxLen, dp[i]);
        }

        // 返回最长递增子序列的长度
        return maxLen;
    }
}