20. TiNO-Edit: Timestep and Noise Optimization for Robust Diffusion-Based Image Editing
该文通过对扩散模型中添加噪声的时刻
t
k
t_k
tk和噪声
N
N
N进行优化,提升SD等文生图模型的图像编辑效果。作者指出现有的方法为了提升文生图模型的图像编辑质量,通常是引入更多的条件信息,如编辑指令(InstructPix2Pix)、边缘图、分割图(ControlNet)等。而较少有人关注扩散模型中的两个关键超参数,时刻
t
k
t_k
tk和噪声
N
N
N,对于编辑效果的影响。因此,作者专门探索了这两个参数对于编辑效果的影响,并且提出一种自动寻找最优参数的优化方法。

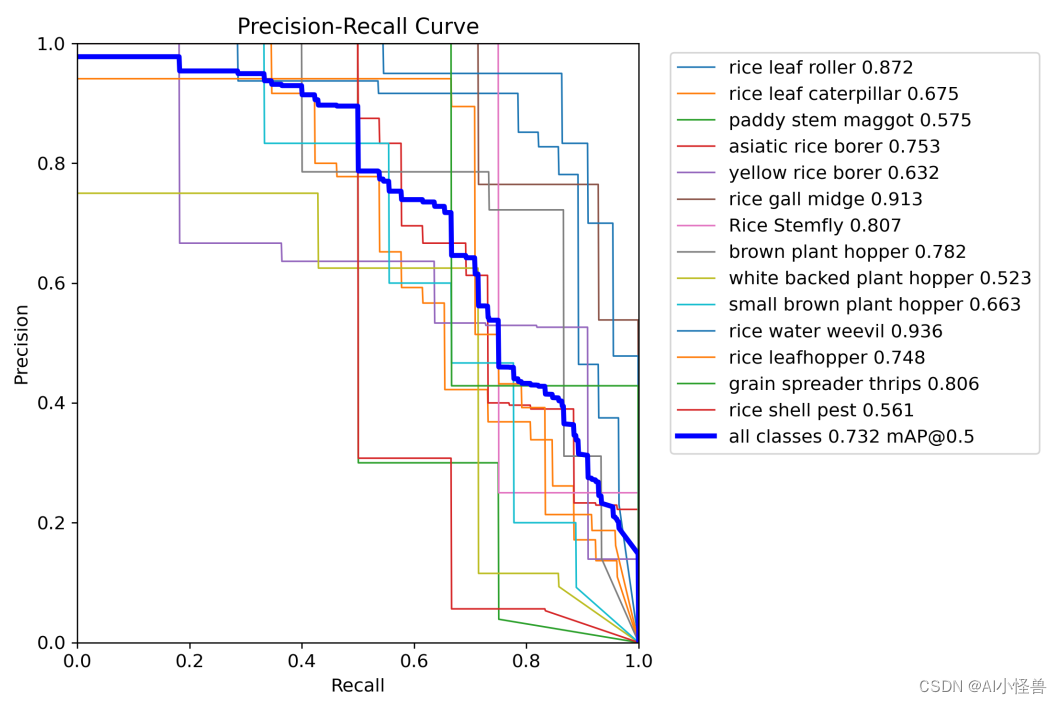
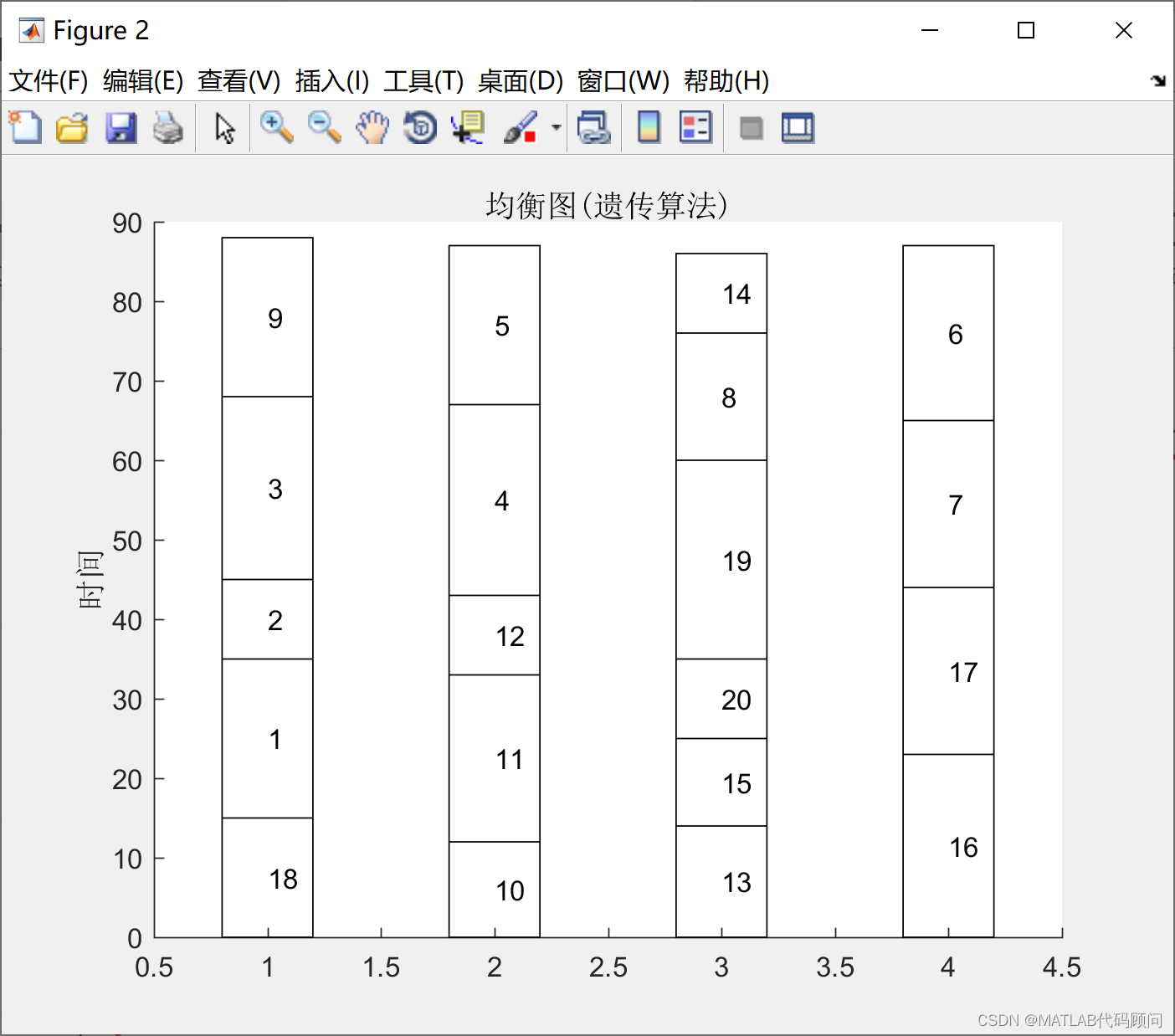
如上图所示,当把一个猫的图片和一个“a photo of dog”的文本描述输入到SD模型中进行Img2Img的转换时,扩散过程的最终时刻
T
T
T(每一列代表一个T)和随机噪声
N
N
N(每一行代表一种N)的选择都会对转换结果产生显著影响。具体而言,随着扩散过程不断的增长,最终生成的结果会越来越接近文本提示的目标结果,而与原本输入的图像越来越无关,这一洞见在SDEdit这篇论文中也有提及。而选择不同的随机噪声,则会生成完全不同的结果。
基于上述的观察结果,不同于直接找到一个适用于所有情况的最优的
T
T
T和
N
N
N,TiNO-Edit的目的是实现
T
T
T和
N
N
N相关参数优化过程的自动化。具体而言,就是现有方法都是预先给定相关的参数,然后对每个样本的扩散和生成过程都采用相同的参数。而TiNO-Edit是在每个样本的扩散和生成过程中都加入了一个优化过程,能够自动地寻找最优的时间和噪声参数,使输出的结果达到最佳,可以理解为一个参数自适应的操作。
在实现过程中,作者并不是直接对扩散过程的最终时刻
T
T
T进行优化,而是对每次加入噪声的时刻
t
k
=
k
T
K
,
k
∈
[
1
,
K
]
t_k=k\frac{T}{K},k\in[1,K]
tk=kKT,k∈[1,K]进行优化。其中
T
∈
[
0
,
1
]
T\in[0,1]
T∈[0,1]表示最终时刻,
K
K
K相当于把时刻
[
0
,
T
]
[0,T]
[0,T]离散为
K
K
K个时间点,从中随机选取第
k
k
k个时间点
t
k
t_k
tk作为添加噪声的时刻。此外还对初始化的随机噪声
N
∼
N
(
0
,
I
)
N\sim \mathcal{N}(0,I)
N∼N(0,I)进行优化。优化过程如下图所示

输入信息包括:原始输入图像
I
I
I, 原始输入图像的文字描述
p
p
p,目标提示
p
O
p_O
pO和其他输入
A
=
{
I
∗
M
a
,
∗
∈
{
r
,
s
,
c
}
}
\mathcal{A}=\{I_*M_a,*\in\{r,s,c\}\}
A={I∗Ma,∗∈{r,s,c}},
M
a
M_a
Ma表示添加物体的掩码,
I
r
I_r
Ir表示图像编辑的参考引导图像,
I
s
I_s
Is表示涂鸦引导图像,
I
c
I_c
Ic表示图像组成(Image Composition)。然后,对
K
K
K,
T
T
T,
t
k
t_k
tk和
N
N
N等参数进行初始化,由于TiNO-Edit是对SD这类潜在的扩散模型进行优化,因此需要将输入图像
I
I
I先经过一个变分自动编码器
V
A
E
e
n
c
{VAE}_{enc}
VAEenc映射到潜在空间中,得到潜在特征
L
L
L。
M
S
K
MSK
MSK表示一种掩码操作,是根据编辑任务只对图像中需要编辑的位置进行掩码,而保持其他位置不变。
W
W
W表示参数优化迭代的次数,
F
D
FD
FD表示前向扩散过程,
R
D
RD
RD表示反向采样过程。在每次迭代过程中,都要完成一次完整的扩散和采样过程,并根据目标函数
L
t
o
t
a
l
\mathcal{L}_{total}
Ltotal对
t
k
t_k
tk和
N
N
N进行优化,最终将最优的采样结果
L
~
0
\tilde{L}_0
L~0进行解码得到目标图像。
目标函数
L
t
o
t
a
l
\mathcal{L}_{total}
Ltotal计算方式如下
L
total
(
L
,
L
~
0
,
p
O
,
p
,
A
)
=
λ
sem
⋅
L
sem
(
L
,
L
~
0
,
p
O
,
p
)
+
λ
ref
⋅
L
ref
(
L
,
L
r
)
+
λ
perc
⋅
L
perc
(
L
,
L
~
0
)
,
\begin{array}{l} \mathcal{L}_{\text {total }}\left(L, \tilde{L}_{0}, p_{O}, p, \mathcal{A}\right) \\ =\lambda_{\text {sem }} \cdot \mathcal{L}_{\text {sem }}\left(L, \tilde{L}_{0}, p_{O}, p\right) \\ +\lambda_{\text {ref }} \cdot \mathcal{L}_{\text {ref }}\left(L, L_{r}\right) \\ +\lambda_{\text {perc }} \cdot \mathcal{L}_{\text {perc }}\left(L, \tilde{L}_{0}\right), \end{array}
Ltotal (L,L~0,pO,p,A)=λsem ⋅Lsem (L,L~0,pO,p)+λref ⋅Lref (L,Lr)+λperc ⋅Lperc (L,L~0),其中,
L
sem
\mathcal{L}_{\text {sem }}
Lsem 表示语义损失,计算方法为
L
sem
(
L
,
L
~
0
,
p
O
,
p
)
=
cos
(
LatentCLIP
vis
(
L
)
,
LatentCLIP
vis
(
L
~
0
)
)
−
cos
(
CLIP
text
(
p
O
)
,
CLIP
text
(
p
)
)
,
\begin{aligned} & \mathcal{L}_{\text {sem }}\left(L, \tilde{L}_{0}, p_{O}, p\right) \\ = & \cos \left(\operatorname{LatentCLIP}_{\text {vis }}(L), \operatorname{LatentCLIP}_{\text {vis }}\left(\tilde{L}_{0}\right)\right) \\ & -\cos \left(\operatorname{CLIP}_{\text {text }}\left(p_{O}\right), \operatorname{CLIP}_{\text {text }}(p)\right), \end{aligned}
=Lsem (L,L~0,pO,p)cos(LatentCLIPvis (L),LatentCLIPvis (L~0))−cos(CLIPtext (pO),CLIPtext (p)),
LatentCLIP
vis
\operatorname{LatentCLIP}_{\text {vis }}
LatentCLIPvis 是一种视觉编码器,根据输入的潜在特征
L
L
L,输出与原始图像
I
I
I的CLIP特征
CLIP
(
I
)
\text{CLIP}(I)
CLIP(I)相似的特征。说白了就是原本的CLIP模型是直接对图像
I
I
I进行编码的,而这里作者输入的是潜在特征
L
L
L,为了适应这一改变,作者专门训练了一个
LatentCLIP
\text{LatentCLIP}
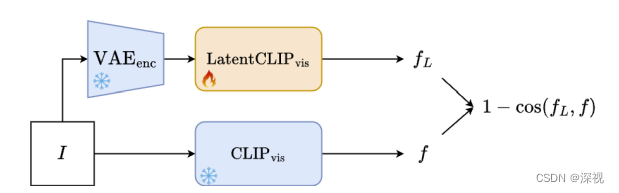
LatentCLIP模型,让其根据
L
L
L输出与
CLIP
(
I
)
\text{CLIP}(I)
CLIP(I)接近的特征图,其训练过程如下
CLIP
text
\operatorname{CLIP}_{\text {text }}
CLIPtext 就表示原始的CLIP文本编码器。
L
ref
\mathcal{L}_{\text {ref }}
Lref 表示参考图像特征
L
r
L_r
Lr与输入图像特征
L
L
L之间的余弦相似性,
L
ref
(
L
,
L
r
)
=
cos
(
LatentCLIP
vis
(
L
)
,
LatentCLIP
vis
(
L
r
)
)
\mathcal{L}_{\text {ref }}\left(L, L_{r}\right) =\cos \left(\operatorname{LatentCLIP}_{\text {vis }}(L), \operatorname{LatentCLIP}_{\text {vis }}\left({L}_{r}\right)\right)
Lref (L,Lr)=cos(LatentCLIPvis (L),LatentCLIPvis (Lr))
L
perc
\mathcal{L}_{\text {perc }}
Lperc 表示输入的特征
L
L
L和生成结果的特征
L
~
0
\tilde{L}_{0}
L~0之间的视觉相似性,
L
perc
(
L
,
L
~
0
)
=
∥
LatentVGG
(
L
)
,
LatentVGG
(
L
~
0
)
∥
1
\mathcal{L}_{\text {perc }}\left(L, \tilde{L}_{0}\right)=\|\operatorname{LatentVGG}(L), \operatorname{LatentVGG}\left(\tilde{L}_{0}\right)\|_1
Lperc (L,L~0)=∥LatentVGG(L),LatentVGG(L~0)∥1
LatentVGG
\operatorname{LatentVGG}
LatentVGG与
LatentCLIP
vis
\operatorname{LatentCLIP}_{\text {vis }}
LatentCLIPvis 的训练过程类似,只是把CLIP的图像编码器换成了VGG。
经过上述的优化训练过程,TiNO-Edit在多个图像编辑任务中的确取得了优于其他方法的效果,可视化结果对比如下
纯文本引导

参考图像引导

涂鸦引导