系列文章目录
前言
一、关键惯性约定
Simscape 多体软件在惯性定义中采用了一系列约定。请注意这些约定,因为如果手动进行惯性计算,这些约定可能会影响计算结果。如果您的惯性数据来自 CAD 应用程序或其他第三方软件,这些约定还可能影响到您需要对惯性数据进行哪些额外处理。特别是
- 惯性积的定义采用负数式,即在质量积分中明确插入减号。还有另一种方法,即在质量积分中不带减号。回想一下,惯性积是惯性矩阵的对角线外元素。
- 质量中心是相对于块的本地坐标系定义的。在导入 CAD 图形的实体中,该坐标系通常是 CAD 应用程序在惯性计算中假定的坐标系。但也可以修改实体几何文件,使两个坐标系不再匹配。
二、惯性矩阵定义
惯性矩阵捕捉了物质围绕局部坐标系的空间分布,在此称为惯性分辨率坐标系。该坐标系在图中标为 I。它的坐标轴与本地参照系的坐标轴平行,与 R 坐标系端口相关联,并相应地标注为 R。
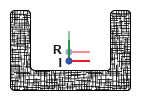
惯性矩阵由惯性矩和惯性积组成。惯性矩占据矩阵的对角线位置,用于测量质量分布在惯性坐标系各轴上的分散度或扩散度。对某一轴线的扩散越大,该轴线对应的惯性矩就越大。
惯性积占据对角线以外的位置,衡量质量分布相对于惯性坐标系平面的不对称程度。对某平面的不对称程度越大,与该平面内任何轴相关的惯性积就越大。下图说明了这些关系。
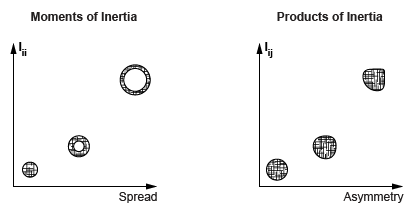
2.1 惯性方程
矩阵相对于主对角线是对称的:指数互为倒数的对角线外元素具有相同的值。这一约束条件将惯性的唯一积的数量从原来的六个(所有对角线外位置的惯性积)减少到您必须在一个块中指定的三个(具有唯一指数组合的惯性积):
惯性积 的定义采用了一些 CAD 应用程序所采用的流行的 "负数 "惯例:
其中,ρ 是质量密度,v 是体积,V 是积分的总体积。x 坐标、y 坐标和 z 坐标是从质量中心到质量 ρdv 的无穷小元素的距离矢量的笛卡尔分量。惯性矩 的定义与此类似:
当应用于简单形状(如圆柱形壳和矩形梁)时,这些定义会产生众所周知的代数方程,这些方程通常公布在标准工程表格中。在明确指定惯性参数时,可以参考这些表格。根据 Simscape 多体程序,完整的惯性矩阵为
2.2 惯性主轴
惯性矩的定义是正数。但是,惯性积可以是正、负或零。如果惯性坐标系的轴恰好与惯性主轴重合,则惯性积为零。惯性矩被称为主惯性矩,惯性矩阵被称为对角矩阵:
在这种情况下,必须指定的非三维惯性矩阵元素的数量减少到三个,即主惯性力矩。因此,惯性主轴可以作为指定惯性矩阵元素的方便坐标系。这就是实体块高度对称的预设形状中所假定的惯性分辨率坐标系。
但是,挤压实体或旋转实体的实体形状一般不采用这种方式,通过 STEP 或 STL 文件导入的实体形状也不采用这种方式。在 "挤压实体 "和 "旋转实体 "形状中,坐标系的位置与您如何定义几何截面密切相关。对于导入的形状,则取决于相对于本地零坐标,零件几何形状是如何建模的。
作为最佳实践,在明确指定惯性矩阵元素时,尤其是使用实体块时,应始终考虑分辨率惯性坐标系的位置。坐标系的位置始终是质量中心的位置,但在使用实体块时,其相对于实体几何体的方向不一定总是与惯性主轴重合。
试试看 指定自定义惯性
考虑图中所示的矩形梁。确定其质量、质心、惯性矩和惯性积。使用自定义惯性参数化,在砖实体块中明确指定计算参数。
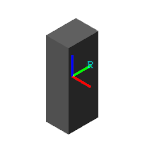
材料和尺寸。 假设结构为铝,相应的质量密度为 0.09754 磅/英寸^3。使用横梁尺寸:
- 宽度 x = 3 英寸
- 高度 y = 4 英寸
- 长度 z = 10 英寸
准备梁模型。 在 Simscape 多体模型中添加实体砖块。在 "Brick Solid 块 "对话框中指定梁的几何形状:将 "几何形状 > 尺寸 "参数设置为 [3 4 10] 英寸。该数组与梁的尺寸 [x y z] 相对应。
几何类型会影响局部参考系(R)的坐标,从而影响惯性计算本身。在可视化工具条中,单击 "坐标系可见性切换 "按钮。坐标系 R 位于质量中心,其轴线平行于梁尺寸(x、y 和 z)。
指定惯性参数。 根据梁的密度和尺寸计算惯性参数。然后在实体砖块参数的惯性部分指定计算值:
- Mass - 质量密度 (ρ) 与体积 (x - y - z) 的乘积:
- Center of Mass - 相对于本地坐标系 (R) 的中心点坐标:
- Moments of Inertia - 来自与分辨率惯性坐标系 (I) 有关的标准表达式:
- Products of Inertia - 由相对于分辨率(I)的惯性坐标系的对称性而来:
三、作为惯性数据源的 CAD
CAD 应用程序通常会为零件模型提供惯性数据。例如,SolidWorks 软件通过其 "质量属性 "工具提供惯性数据,Onshape 软件通过其相同工具的版本提供惯性数据。您可以在 Simscape 多体环境中引用这些数据并手动指定。
3.1 替代惯性约定
某些 CAD 应用程序(包括 SolidWorks)使用另一种惯性约定来定义惯性矩阵的元素。这种约定去掉了惯性积定义中的负号。例如,惯性积 Iyz 变为
如果您的惯性数据源采用此约定,则必须在 Simscape 多体环境中指定惯性积的值之前明确否定惯性积。例如,SolidWorks 的惯性矩阵为
要在 Simscape 多体环境中正确指定矩阵元素,必须按以下方式处理它们:
3.2 CAD 导入替代方案
您可以将 CAD 装配模型导入 Simscape 多体环境,而不是引用 CAD 装配模型中的惯性数据。CAD 导入基于 smimport 功能,该功能可解析 XML 格式的多体描述文件,并生成包含所有预设块参数(包括惯性参数)的等效框图。
在导入 CAD 模型之前,您必须以有效的 XML 格式导出模型,即符合 Simscape Multibody XML 模式的格式。只有当您拥有完整的 CAD 装配模型时,此选项才适合您。对于单个 CAD 零件,请使用实体块的 STEP 文件导入功能,并将 "惯性">"类型 "参数设置为 "从几何图形计算"。
更多信息,请参阅将 CAD 装配体转换为 Simscape 多体模型。
试试看: 参考 SolidWorks 模型
确定图中所示 L 形梁的惯性参数。然后,通过将惯性参数化设置为自定义,在实体块中明确指定这些参数。将本示例中提供的质量属性数据用于梁的 SolidWorks 模型。
打开实体模型。 在 MATLAB® 命令提示符下输入 openExample("sm/DocLBeamInertiaExample")。此时将打开一个简单模型,其中的文件实体块代表 L 形梁实体。打开文件实体块并查看其几何参数。梁的几何体是从之前从 SolidWorks 模型导出的 STEP 文件中导入的。该几何体为
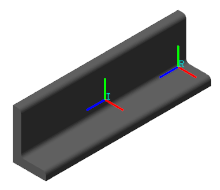
在可视化窗格中,单击 "切换坐标系可见性 "按钮。可视化窗格显示两个坐标系,一个标为 R,另一个标为 I。
坐标系 R 是实体的局部坐标系。它与 SolidWorks 用户所说的零件模型输出坐标系相吻合。该坐标系位于横梁两个纵向端点之一 L 形的下角。您必须指定相对于该坐标系的质心。
坐标系 I 是为方便您使用而定制的实体坐标系。该坐标系与分辨率惯性坐标系一致。其原点位于质量中心,轴线与本地坐标系的轴线平行。您必须指定相对于该坐标系的惯性矩和惯性积。
查看 SolidWorks 数据。 SolidWorks 模型为 L 型梁零件提供了以下质量属性数据:
Mass properties of l_beam_solid
Configuration: Default
Coordinate system: -- default --
Density = 0.10 pounds per cubic inch
Mass = 2.19 pounds
Volume = 22.41 cubic inches
Surface area = 101.91 square inches
Center of mass: ( inches )
X = 0.58
Y = 1.08
Z = 5.00
Principal axes of inertia and principal moments of inertia:
( pounds * square inches )
Taken at the center of mass.
Ix = ( 0.00, 0.00, 1.00) Px = 2.49
Iy = ( 0.38, -0.92, 0.00) Py = 18.65
Iz = ( 0.92, 0.38, 0.00) Pz = 20.35
Moments of inertia: ( pounds * square inches )
Taken at the center of mass and aligned with
the output coordinate system.
Lxx = 20.10 Lxy = -0.60 Lxz = 0.00
Lyx = -0.60 Lyy = 18.89 Lyz = 0.00
Lzx = 0.00 Lzy = 0.00 Lzz = 2.49
Moments of inertia: ( pounds * square inches )
Taken at the output coordinate system.
Ixx = 77.40 Ixy = 0.76 Ixz = 6.33
Iyx = 0.76 Iyy = 74.39 Iyz = 11.79
Izx = 6.33 Izy = 11.79 Izz = 5.76数据包括质心相对于 "输出坐标系 "的坐标。该坐标系与相应 Simscape 多体实体的局部坐标系 (R) 相吻合。
数据还包括 "取自质量中心并与输出坐标系对齐 "的惯性矩和惯性积矩阵。该坐标系与 Simscape 多体实体的惯性分辨率 (I) 坐标系一致。
指定惯性参数。 展开 "文件实体块 "对话框的 "惯性参数 "部分。然后将 "惯性 > 类型 "参数设置为 "自定义",更改惯性参数设置。此时将显示整套惯性参数供您指定。
- 将 "质量 "参数设置为 2.19 磅。
- 将质量中心参数设置为 [0.58 1.08 5.00] in. 这是 SolidWorks 报告中显示的质量中心的 [x y z] 坐标。
- 将惯性力矩参数设置为 [20.10 18.89 2.49] lbm*in^2。这些是 SolidWorks 报告中显示的 [Lxx Lyy Lzz] 惯性矩。
- 将惯性积参数设置为 [0 0 0.6] lbm*in^2。这些是 SolidWorks 报告中显示的惯性积的负 [Lyz Lzx Lxy ]。
四、自动惯性计算
实体块提供了一个选项,可根据实体几何图形自动计算大部分惯性参数。该选项可从 "惯性">"类型 "下拉列表中选择,默认为打开,您只需指定几何参数和质量或质量密度。
程序块使用几何参数和质量参数计算其余惯性参数--质心、惯性矩和惯性积--相对于相应的坐标系。计算基于质量密度恒定且均匀的假设。
您可以在实体块内名为 "显示惯性 "的可扩展部分查看计算结果。质心是相对于本地坐标系(R)给出的,惯性矩和惯性积是相对于惯性分辨率坐标系(I)给出的。这些都是您可以指定这些参数的坐标系。
试试看 显示惯性计算结果
配置 DocLBeamInertiaExample 模型的文件实体块,根据实体几何形状及其质量密度计算惯性参数。然后,查看计算参数。
- 在 "文件实体 "块的对话框中,将 "惯性">"类型 "参数切换为 "从几何体计算"。密度参数下方会出现一个显示惯性节点。
- 将密度参数设置为 0.09754 lbm/in^2。该值对应于铝结构实体,与 "查看 SolidWorks 数据 "中提供的 SolidWorks 数据中的假设相同。
- 展开 "显示惯性 "节点并单击 "更新 "按钮。显示惯性 "下的惯性参数将以计算值填充。将它们与 SolidWorks 质量属性数据中提供的值进行比较。

五、URDF 中的惯性矩阵
5.1 长方体的惯性矩阵
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
#
# SPDX-License-Identifier: Apache-2.0
# Copyright 2022 Stéphane Caron
"""
Compute the inertia matrix of a box and print it as URDF.
Source:
https://en.wikipedia.org/wiki/List_of_moments_of_inertia#List_of_3D_inertia_tensors
"""
import argparse
import sys
def parse_command_line_arguments():
parser = argparse.ArgumentParser(description=__doc__)
parser.add_argument("mass", type=float, help="total mass in [kg]")
parser.add_argument(
"l_x", type=float, help="box length in [m] along the x-axis"
)
parser.add_argument(
"l_y", type=float, help="box length in [m] along the y-axis"
)
parser.add_argument(
"l_z", type=float, help="box length in [m] along the z-axis"
)
return parser.parse_args()
if __name__ == "__main__":
args = parse_command_line_arguments()
mass, l_x, l_y, l_z = args.mass, args.l_x, args.l_y, args.l_z
ixx = mass / 12.0 * (l_y ** 2 + l_z ** 2)
iyy = mass / 12.0 * (l_x ** 2 + l_z ** 2)
izz = mass / 12.0 * (l_x ** 2 + l_y ** 2)
print(f'<box size="{l_x} {l_y} {l_z}" />')
print(f'<mass value="{mass}" />')
print(f"\n<!-- {' '.join(sys.argv)} -->")
print(
f'<inertia ixx="{ixx}" ixy="0" ixz="0" '
f'iyx="0" iyy="{iyy}" iyz="0" '
f'izx="0" izy="0" izz="{izz}" />'
)
5.2 圆柱体的惯性矩阵
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
#
# SPDX-License-Identifier: Apache-2.0
# Copyright 2022 Stéphane Caron
"""
Compute the inertia matrix of a cylinder and print it as URDF.
Source:
https://en.wikipedia.org/wiki/List_of_moments_of_inertia#List_of_3D_inertia_tensors
"""
import argparse
import sys
def parse_command_line_arguments():
parser = argparse.ArgumentParser(description=__doc__)
parser.add_argument("mass", type=float, help="total mass in [kg]")
parser.add_argument(
"radius", type=float, help="radius in [m] in the xy-plane"
)
parser.add_argument(
"length", type=float, help="length in [m] along the z-axis"
)
return parser.parse_args()
if __name__ == "__main__":
args = parse_command_line_arguments()
mass, radius, length = args.mass, args.radius, args.length
ixx = mass / 12.0 * (3 * radius ** 2 + length ** 2)
iyy = mass / 12.0 * (3 * radius ** 2 + length ** 2)
izz = mass / 2.0 * radius ** 2
print(f'<cylinder radius="{radius}" length="{length}" />')
print(f'<mass value="{mass}" />')
print(f"\n<!-- {' '.join(sys.argv)} -->")
print(
f'<inertia ixx="{ixx}" ixy="0" ixz="0" '
f'iyx="0" iyy="{iyy}" iyz="0" '
f'izx="0" izy="0" izz="{izz}" />'
)