前言

        又碰到了约瑟夫问题，这样的题目本来用环形链表模拟的话就能做出来。然而，最近新学习了一种做法，实在是有点震惊到我了。无论是思路上，还是代码量上，都是那么的精彩。就想也震惊一下其他人。谁能想到原来模拟出来四五十行代码，如今只需要三行就搞定了呢？

一. 题目

        题目和约瑟夫问题的意思相同，读者可酌情跳过。

描述

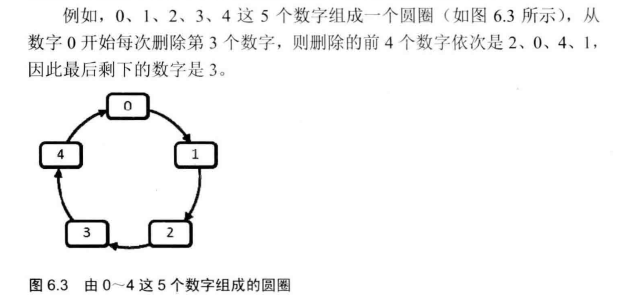
    每年六一儿童节，牛客都会准备一些小礼物和小游戏去看望孤儿院的孩子们。其中，有个游戏是这样的：首先，让 n 个小朋友们围成一个大圈，小朋友们的编号是0~n-1。然后，随机指定一个数 m ，让编号为0的小朋友开始报数。每次喊到 m-1 的那个小朋友要出列唱首歌，然后可以在礼品箱中任意的挑选礼物，并且不再回到圈中，从他的下一个小朋友开始，继续0... m-1报数....这样下去....直到剩下最后一个小朋友，可以不用表演，并且拿到牛客礼品，请你试着想下，哪个小朋友会得到这份礼品呢？

数据范围：1≤𝑛≤50001≤n≤5000，1≤𝑚≤100001≤m≤10000

要求：空间复杂度 𝑂(1)O(1)，时间复杂度 𝑂(𝑛)O(n)

二. 解题思路

1. 传统解法

        传统接法就是环形链表模拟，先将链表链接好，然后再遍历链表到了 m 次就删除数据。循环直到剩下一个节点。

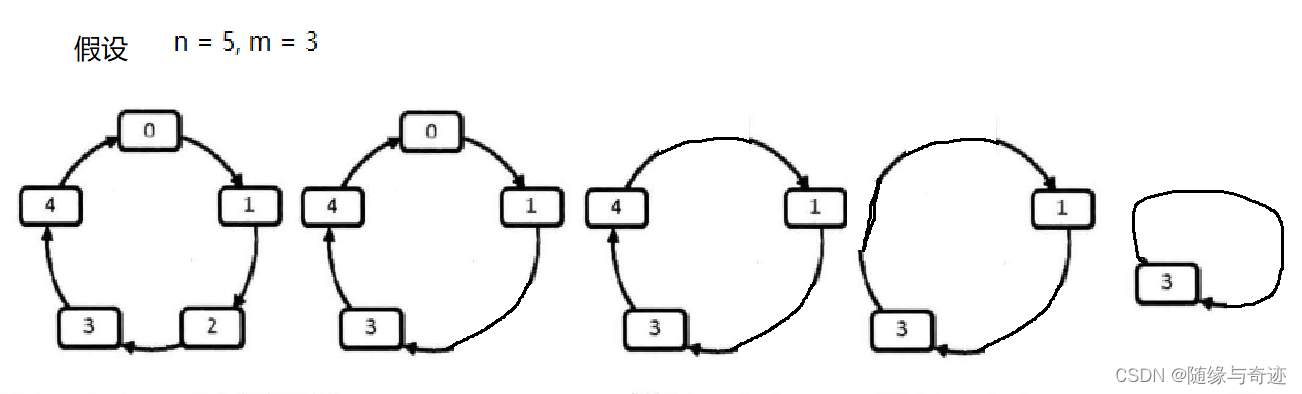
图1-1

        如此得到最后剩下的人是3号。

2. 递推解法

        这个解法就比较有意思了，重点讲讲。

       首先我们从最开始 n 个人的时候开始模拟，n 个人里面第 （m - 1）% n 号会出局，剩下的人从原来第 m 个开始从 0 编号。

图2-1

        假设在 n 个人，报数为 m 的时候，最后留下的人用 dp[n] 表示。n - 1 个人的时候， 最后留下的人用 dp[n - 1] 表示。

        那么，dp[n] 与 dp[n - 1] 的关系是什么呢？

        dp[n] = dp[n - 1] + m

        实际上由于 dp[n] 的大小不能超过 n - 1。如图2-1左侧，所以最后结果需要取模。

        dp[n] = （dp[n - 1] + m）% n 

图2-2

        依次类推从只有一个人的时候开始向人多了推算，只有一个人的时候恒成立 dp[1] = 0 .

        根据公式 dp[2] = （dp[1] + m）% 2 ，依次向下计算即可。

        然后回到传统解法的例子，验证：

图1-1

        dp[1] = 0 ，

        dp[2] = （dp[1] + 3）% 2 = 1 ，

        dp[3] = （dp[2] + 3）% 3 = 1，

        dp[4] = （dp[3] + 3）% 4 = 0，

        dp[5] = （dp[4] + 3）% 5 = 3，

        结果竟然和传统的模拟解法结果一样，太神奇了。

三. 解题代码

int LastRemaining_Solution(int n, int m ) {
    int f = 0;
    for(int i = 2; i <= n; ++i)
    {
        f = (f + m) % i;
    }
    return f;
}

        就这么多，核心代码就三行，不要太爽。

作者结语

        无敌的算法是真的能出奇迹，数学无敌。