具体代码实现在gitee：登录 - Gitee.com

目录

具体代码实现在gitee：登录 - Gitee.com

1.非递归实现的快速排序算法。

第一步 首先要创建一个栈

第二步紧接着进行入栈，出栈，弹出栈顶元素，获取栈顶元素，判空，销栈等操作；

第三步快速排序算法的分区

最后实现

运行结果

2.非递归实现的归并排序算法

 代码解析

代码实现 

运行结果

---

1.非递归实现的快速排序算法。

第一步 首先要创建一个栈

typedef struct Stack//创建一个栈
{
    int* data;//存储栈中的元素的数组指针
    int top;//栈顶元素在数组中的索引位置
    int capacity;//栈的容量，即数组的大小
} ST;

第二步紧接着进行入栈，出栈，弹出栈顶元素，获取栈顶元素，判空，销栈等操作；

void STInit(ST* s)//入栈
{
	s->data = NULL;
	s->top = -1;
	s->capacity = 0;
}

void STPush(ST* s, int val)//出栈
{
	if (s->top == s->capacity - 1)
	{
		int newCapacity = s->capacity == 0 ? 4 : s->capacity * 2;
		int* newData = (int*)realloc(s->data, newCapacity * sizeof(int));
		if (newData == NULL)
		{
			// 内存分配失败处理
			return;
		}
		s->data = newData;
		s->capacity = newCapacity;
	}
	s->data[++s->top] = val;
}

void STPop(ST* s)//用于弹出栈顶元素，即将top的值减1，表示栈顶位置往下移动一位。
{
	if (s->top >= 0)
		--s->top;
}

int STTop(ST* s)//于取栈顶元素的值
{
	if (s->top >= 0)
		return s->data[s->top];
	return -1; // 栈为空时的处理，这里返回-1表示栈为空
}

int STEmpty(ST* s)//判断栈是否为空
{
	return s->top == -1;
}

void STDestroy(ST* s)//销毁栈
{
	free(s->data);
	s->data = NULL;
	s->top = -1;
	s->capacity = 0;
}

第三步快速排序算法的分区

具体过程可见快排：http://t.csdnimg.cn/yZnPT

它的作用是将数组a的一部分元素进行分区，使得分区后的左边元素都小于或等于key，右边元素都大于或等于key。

int PartSort3(int* a, int left, int right)
{
	int key = a[left];
	while (left < right)
	{
		while (left < right && a[right] >= key)
			--right;
		a[left] = a[right];
		while (left < right && a[left] <= key)
			++left;
		a[right] = a[left];
	}
	a[left] = key;
	return left;
}

最后实现

下是该代码的具体实现步骤：

1. 创建一个栈ST，并初始化为空。
2. 将结束索引end和开始索引开始依次入栈ST。
3. 进入循环，直到栈ST为空： a. 从栈ST中弹出两个索引，分别赋值给left和right。 b. 调用PartSort3函数，将数组a在[left， right]范围内进行三路划分，返回划分后的基准元素的索引keyi。 c. 如果left < keyi - 1，则将keyi - 1和left依次入栈ST，用于后续处理[left， keyi-1]范围内的子数组。 d. 如果keyi + 1 < right，则将right和keyi + 1依次入栈ST，用于后续处理[keyi+1， right]范围内的子数组。
4. 循环结束后，销毁栈ST。

void QuickSortNonR(int* a, int begin, int end)
{
	ST s;
	STInit(&s);
	STPush(&s, end);
	STPush(&s, begin);

	while (!STEmpty(&s))
	{
		int left = STTop(&s);
		STPop(&s);
		int right = STTop(&s);
		STPop(&s);

		int keyi = PartSort3(a, left, right);
		// [left, keyi-1] keyi [keyi+1, right]
		if (left < keyi - 1)
		{
			STPush(&s, keyi - 1);
			STPush(&s, left);
		}

		if (keyi + 1 < right)
		{
			STPush(&s, right);
			STPush(&s, keyi + 1);
		}
	}

	STDestroy(&s);
}

运行结果

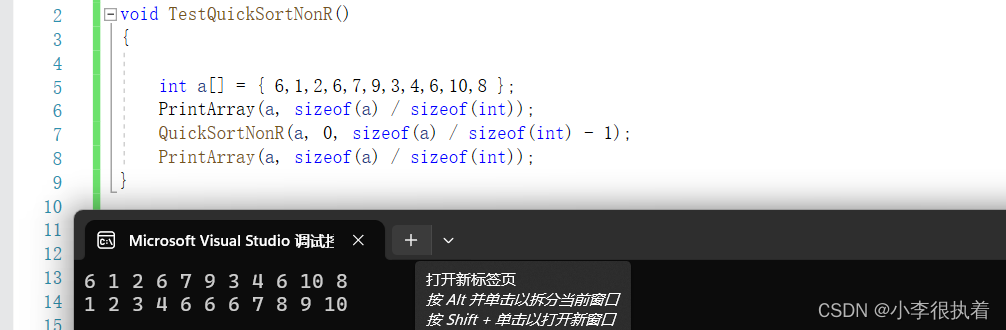
2.非递归实现的归并排序算法

 代码解析

1. 首先使用malloc函数申请了一个临时数组tmp，用于存储排序过程中的中间结果。

2. 定义了变量gap，初始值为1，代表待合并的两个子数组的长度。

3. 使用while循环，当gap小于数组长度n时，进行合并操作。

4. 在每次循环中，通过for循环将数组分成若干个长度为gap的子数组，每次有两个子数组进行合并。

5. 定义四个变量begin1, end1, begin2, end2，分别表示第一个子数组的起始位置、结束位置，以及第二个子数组的起始位置、结束位置。

6. 如果end1大于等于数组长度n，或者begin2大于等于数组长度n，说明已经没有需要合并的子数组了，跳出for循环。

7. 如果end2大于等于数组长度n，将end2的值设置为n-1，保证不会数组越界。

8. 使用while循环，将begin1和begin2所指向的元素进行比较，并将较小的元素赋值给tmp数组，然后移动指针。

9. 如果begin1仍然小于等于end1，说明第一个子数组还有剩余元素，将剩余元素复制到tmp数组中。

10. 如果begin2仍然小于等于end2，说明第二个子数组还有剩余元素，将剩余元素复制到tmp数组中。

11. 使用memcpy函数将tmp数组中的数据复制回原数组a中。

12. 每次合并完成后，将gap乘以2，继续下一轮合并。

13. 最后使用free函数释放临时数组tmp的内存空间。

代码实现 

void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail");
		return;
	}

	int gap = 1;
	while (gap < n)
	{
		for (size_t i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;
			
			if (end1 >= n || begin2 >= n)
			{
				break;
			}

			if (end2 >= n)
			{
				end2 = n - 1;
			}

			int j = begin1;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}

			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}

			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}

			memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
		}

		gap *= 2;
	}


	free(tmp);
}

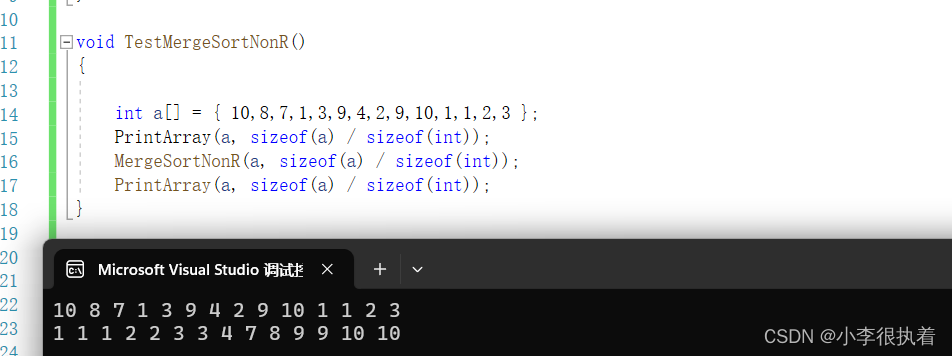
运行结果