前言

在做加、减、乘、除等运算时，经常会发生 溢出 的情况。比如1个4bits的计数器（每个时钟累加1），在4’b1111 + 1 后，原本其期望值应该是 15+1 即16，但是4bits的寄存器能表示的最大值只是4‘b1111即15，所以它的值 溢出 了。 防止产生错误溢出的机制，就是所谓的 溢出保护。

为了使运算结果不错误溢出从而导致功能错误，我们应该对运算结果的位宽进行合理的扩展，使其在不浪费资源的情况下保证运算结果的正确性。位宽选择的少了，那么就容易溢出；位宽选择的多了，又容易浪费电路面积。位宽的扩展比较复杂，不同的情况应具体判断，不能一概而论。

---

是不是所有溢出都需要保护？

先说结论，不是所有的溢出都需要保护的。举两个典型例子：1、计数器；2、补码加法。

计数器中的溢出

假设要设计的是这样一个计数器：

每个时钟周期累加1，从0~15循环计数。

为此可以写如下伪代码：

//代码1：带清零操作
always@(posedge clk）
begin
	if(cnt == 4'd15 )
		cnt <= 4'd0;
	else 
		cnt <= cnt + 4'd1;
end

我相信大多人都不会写这个代码，因为它对cnt的清零操作完全是多余的。实际上，这样写就完全足够：

//代码2：不带清零操作
always@(posedge clk）
	cnt <= cnt + 4'd1;
end

代码2的潜在逻辑是：利用 溢出 完成了原本的清零操作。当cnt为4’d15时，它的加1操作的结果是16即1_0000。因为16的表示需要5bits的位宽，所以它的最高位被截掉了，只剩下了低位的0000，即4’d0。利用了溢出机制的代码2生成的电路是要比代码1生成的电路要小的，因为代码1电路会多一个比较逻辑电路和选择逻辑电路。

可以看到，这样的溢出不光不需要采取保护措施，反而还能减小设计电路的面积。当然，只能是从最小值计数到最大值的计数器（反着来的也可以）才能合理利用溢出机制，只计数到中间值的计数器显然不行。比如，从0计数到10，就无法利用溢出，只能老老实实用比较器来判断。

补码加法中的溢出

补码本身就是一种利用 溢出 的编码机制，它可以使得减法转化成加法：即减去一个数等价于加上一个数。例如：

将算式 7 - 3 =4 转换成补码加法，等价于：7 + (-3) = 4。

保留溢出的情况下，结果是1_0100，解释成有符号数就是 -12，这显然是错的。但如果舍去溢出位，那么结果是0100，即解释成有符号数的结果是 4，结果正确。为什么呢？

舍去溢出位的操作是不是可以看做是一个减法？对于这个例子来说，就是减5‘b1_0000即16。然后 -3 的补码如果将其看做是一个无符号数是不是就是4’b1101，即13。那么整个算式实际上就转化成了：

7 - 3 = = 7 + (-3) = 7 + 13 - 16 = 7 - （16 - 13）

利用溢出机制和补码机制，就把减法操作给转换成了加法操作。

---

需要做溢出保护的情况

上面的例子讨论的是不需要做溢出保护的情况，下面则例举一些常见的需要做溢出保护的例子。

两个无符号数的加法

这种情况最常见，也最简单。两个无符号数的加法就是两个正数相加，这种情况只要考虑最极端的情况就行了。比如两个4bits的数相加，最极端的情况就是：

4‘b1111 + 4’b1111 = 15 + 15 = 30

30如果还用4bits表示，那么就溢出了，所以需要扩大结果的位宽。能表示30这个数的寄存器的最小位宽是6（2^6 = 32），位宽大于6也能表示30，但就没必要浪费电路面积了。

多个无符号数的加法

这种情况和两个无符号数的加法类似，都是利用极端情况来推断就行了，例如4个4bits的无符号数相加，最极端的情况是：

4‘b1111 + 4’b1111 + 4‘b1111 + 4’b1111 = 15 + 15 + 15 +15 = 60

因为log2（60）≈ 5.9，对结果向上取整，所以需要的最小位宽是6bits。

两个无符号数的减法

两个无符号数的加法可以分成两种情况：

• 减法结果是正数或零
• 减法结果是负数

对于结果是正数或零的情况是不会存在溢出的情况的，因为它的值必然小于被减数，位宽不可能会溢出，所以不需要做什么特殊的处理。

减法结果是负数的情况则麻烦一些，因为负数必然是有符号数，那就意味着最高位只能表示符号而不能再表示数值了。比如：

两个4bits数的减法0 - 1 = -1， 等价于 4’b0000 - 4’b0001 = 4’b0000 + 4’b1111 = 4’b1111，这个值如果看成是有符号数那是-1，结果是正确的，如果看成是无符号是那么是15，结果就是错误的。这样看，似乎只要将减法的结果定义为有符号数即可解决问题，但如此新的问题也会随之而来。

4bits的有符号数和4bits的无符号数的表示范围是不一致的，前者是-8_{7，后者则是0}15。两个4bits的无符号数的减法的取值范围则是：

max（最大 - 最小）： 15 - 0 =15

min（最小 - 最大）: 0-15 = -15

可以看到，仅仅将减法结果改成有符号数仍是无法表示这段范围的，需要将减法结果从4bits扩展到5bits，就可以表示该范围了，5bits有符号数的表示范围是 -16~15。

此类情况的处理办法是将减法结果扩展1bits，防止因为负数结果的产生而导致的错误溢出。如果两个数的位宽一样，那减法结果的位宽应该+1；如果两个数的位宽不一样，那就在位宽大的那个的数的位宽基础上+1。

无符号数的加减混合运算

依然用极限情况来推断运算结果的范围，然后再设计相应的溢出保护即可，例如：

wire [3:0] a;	//0~15
wire [4:0] b;	//0~31
wire [5:0] c;	//0~63
wire [2:0] d;	//0~7
wire [6:0] e;	//0~127

assign sum = a + b + c - d - e;

(a + b + c) 的取值范围是 0 ~109，（d + e）的取值范围是 0 ~134，而sum的取值则范围是 -134 ~ 109，所以其位宽应是9位（-256~255）。当然，这样做的前提条件是所有的运算都在一个式子里完成，所以只需要考虑最后结果的位宽。如果运算是分步完成的，那么就要对每一个中间结果的位宽分别讨论。

两个有符号数的加减法

首先，对于有符号数来说，减法和加法是没有区别的（都可以看做是加法），所以只需要讨论加法的情况即可。

两个有符号数的加法一共有3种情况：

• 正数 + 正数
• 负数 + 负数
• 正数 + 负数

接下来分别讨论：

（1）正数 + 正数

这种情况可能发生溢出，且需要对运算结果进行溢出保护，例如极端情况：

4’d7 + 4’d7 = 4’b0111 + 4’b0111 = 4’b1110

因为最高位的符号位变成了1，导致结果从一个正数(+14)变成了负数(-2)，显然是不对的。如果把结果的位宽扩展1位到5位，那么结果5’b01110就是正确的结果即+14了。

（2）负数 + 负数

这种情况和上一种情况类似，考虑极端情况：

-4’d8 + （- 4’d8） = 4’b1000 + 4’b1000 = 5’b1_0000

如果舍去最高的溢出位，那么结果4‘b0000（0）就是错误的；如果不舍去溢出位，那么结果5’b1_0000(-16)就是正确的，所以这种情况也需要对运算结果进行位扩展以实现溢出保护。

（3）正数 + 负数

一方面，在上一章我们已经讨论过了，正数 + 负数 是要依靠溢出才能正确地实现运算；另一方面，从（正数 + 正数）和（负数 + 负数）的讨论，我们又得出结论：需要扩展位宽以实现对结果的溢出保护。这么看，似乎陷入了死局，何解？

常见的做法是：

对两个加数进行符号位扩展，同时把结果的位宽也扩展一位。

还是上面例子，两个4bits有符号数的加法，应该用Verilog这么写：

wire 	[3:0]	add1,add2;	//有符号数
wire	[4:0]	sum;		//有符号数

assign sum = {add1[3],add1} + {add2[3],add2};	//两个加数都补上最高位的符号位

仍然用上面的例子：

将算式 7 - 3 =4 转换成补码加法，等价与：7 + (-3) = 4。

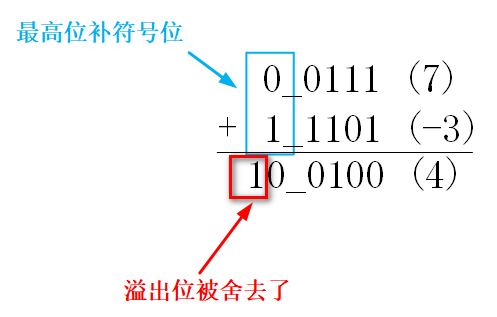
因为结果是5bits，所以最高位（第6位）会被舍去，只留下了5bits的结果5’b00100（4），结果正确。

综合这3种情况，可以得出结论：

对于2个有符号数的加减法，结果的位宽为其中位宽较大者的位宽+1，同时运算时，需要将两个加数的最高位补符号位到与结果位宽相同。

两个无符号数的乘法

假设其中一个数的位宽是a，另一个数的位宽是b，那么积的位宽就是（a + b）。也可以用极限情况来分析，比如两个4bits的无符号数乘法，最大的值是1111 × 1111 = 15 × 15 = 225，那么就是需要8位来表示（2^8 = 256）。其实也可以将乘法看成是移位，15 × 15 ≈ 15 × 16，而乘16相当于作为4bits，所以积的位宽应该是在前者的位宽基础上加上4，即二者的位宽相加。

两个有符号数的乘法

这种情况，积的位宽也是两个乘数的位宽之和。

这样的结果是有点反直觉的，因为两个乘数都有一个符号位，相乘之后这个符号位显然又不需要2bits来表示，那么位宽应该是二者的位宽之和减1才对。造成这一结果的原因是因为有符号数对负数的表示和正数的表示是不对称的，比如4bits的有符号数的表示范围是 -8~7，负数的范围比正数的表示要多一个数（-8），-8的补码是 1000。假设1000不表示 -8，而和0000同样表示0，那么它的范围就变成了 -7~7，此时二者的乘法就是乘数相加，再加一个符号位，即3+3+1 = 7位。

但是很遗憾，1000就是 -8 而不是 - 0 ，所以当两个 -8 相乘的时候，结果就会在6bits的基础上溢出了（-8 × -8 = 64， 即100_0000），再加上符号位，此时积的位宽就需要 6+1+1 = 8位了。

除法

除法的实现是四则基础运算中最麻烦。因为两个整数的除法，其结果可能是小数，比如11/10=1.1，而1.1又是个无法用有限位数就能表示的小数，它涉及到浮点数的定点化问题，不同的方案对定点化的定标要求可能也不一致，所以除法的结果位宽不能用一个统一的标准来判断。

---

限制运算结果位宽的情况

严格来说，这类情况实际上是要解决如何处理数据的溢出，而不仅仅是对结果扩展位宽以防止溢出产生错误。比如2个3bits的无符号数相加，同时限制和的位宽也是3bits，常见的做法有两种：

• 如果有溢出则将和的结果锁定在最大值，比如 3+6 = 9，但是3bits能表示的最大结果是7，所以输出的和就是7。
• 如果有溢出则将溢出舍去，而将低位保留。比如 9 = 3 + 6 = 011 + 110 = 1_001，将溢出的最高位舍去，而将最低位保留，那么和的结果就是001即1。

关于这两种溢出模式的处理，我们在下一篇文章再细说。