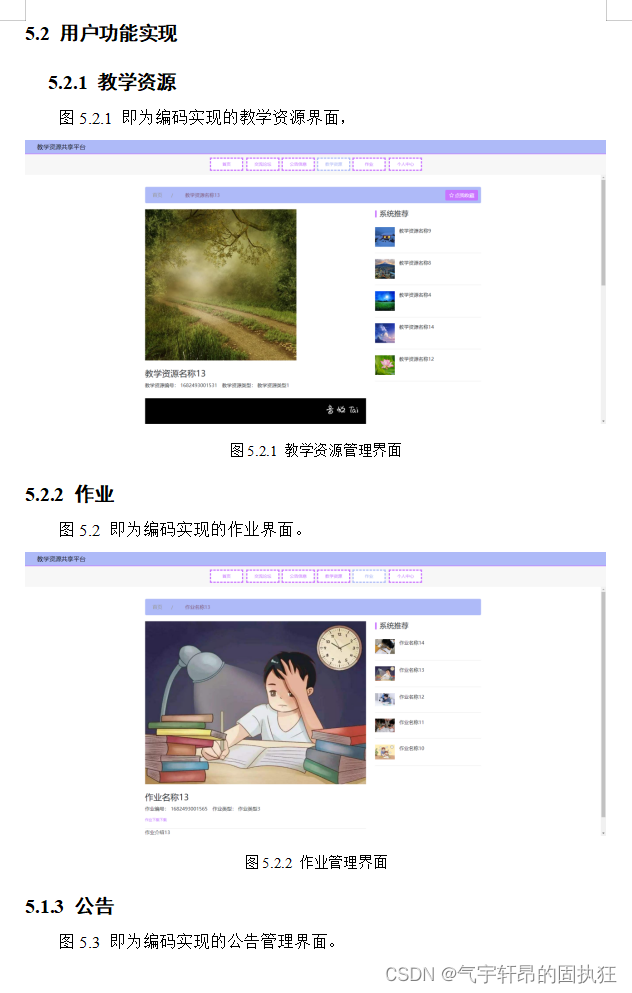
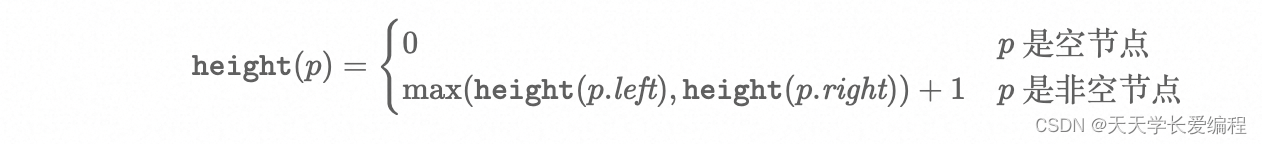思路：

首先使用递归方式求出最优解。从每个房屋开始，分别考虑偷与不偷两种情况，然后递归地对后续的房屋做同样的决策。这种方法确保了可以找到在不触发警报的情况下可能的最高金额。

代码如下：

public static int rob(int[] nums) {
    if (nums == null || nums.length == 0) {
        return 0;  // 如果没有房屋可偷，则返回0
    }
    // 递归求解最大金额
    return process(nums, 0, nums.length);
}

private static int process(int[] nums, int index, int N) {
    if (index >= N) {
        return 0;  // 超出数组范围，返回0
    }
    // 偷当前房屋并跳过下一个房屋
    int p1 = nums[index] + process(nums, index + 2, N);
    // 不偷当前房屋，考虑下一个房屋
    int p2 = process(nums, index + 1, N);
    // 返回两种方案中的最大值
    return Math.max(p1, p2);
}

但是递归方式会有重复计算，知道了思路来改成动态规划就很容易。dp[N]=0,超出长度，dp[n-1]=nums[n-1]表示从n-1开始最优抢多少金额，那只能抢一家。然后开始递归。dp状态转移方程就是Math.max(nums[i] + dp[i + 2], dp[i + 1]);代码如下：

class Solution {
    public static int rob(int[] nums) {
    // 检查输入数组是否为空，如果为空或长度为0，则直接返回0，因为没有什么可以偷的
    if (nums == null || nums.length == 0) {
        return 0;
    }
   // 获取数组的长度，即房屋的数量
    int N = nums.length; 
     // 创建一个动态规划数组，长度为N+1，用来存储到每个房屋为止的最大偷窃金额
    int[] dp = new int[N + 1]; 
    // 数组最后一个元素设为0，表示超过最后一个房屋后没有可偷的金额
    dp[N] = 0;  

    // 初始化最后一间房屋的情况，只有一个选择，就是偷这间房屋
    dp[N - 1] = nums[N - 1];  

    // 从倒数第二个房间开始向前计算每个房间的最大偷窃金额
    for (int i = N - 2; i >= 0; i--) {
         // 如果偷当前房屋i，那么下一个可偷的房屋是i+2，总金额是当前房屋的金额加上dp[i+2]
        int p1 = nums[i] + dp[i + 2]; 
        // 如果不偷当前房屋i，那么考虑从下一个房屋i+1开始的最大金额
        int p2 = dp[i + 1];  

        // 对于当前房屋i，选择偷与不偷的最大值作为dp[i]的值
        dp[i] = Math.max(p1, p2);
    }

    // 返回从第一间房屋开始偷窃的最大金额，即dp数组的第一个元素
    return dp[0];
}

}