🚀Write In Front🚀
📝个人主页:令夏二十三
🎁欢迎各位→点赞👍 + 收藏⭐️ + 留言📝
📣系列专栏:深度学习
💬总结:希望你看完之后,能对你有所帮助,不足请指正!共同学习交流 🖊
文章目录
3.1 神经网络概述
3.2 神经网络的表示
3.3 计算一个神经网络的输出
3.3.1 神经网络的符号惯例
3.3.2 神经网络的计算
3.4 多样本向量化
3.5 向量化实现的解释
3.6 激活函数
3.11 随机初始化
3.1 神经网络概述
本周的学习目标是实现一个神经网络,现在我们预览一下这周将要学习的内容。
上面讲了逻辑回归模型,也就是多个输入进入一个模型中,得到一个输出,由于模型中包含Sigmoid函数,因此输出为 0 或 1 。
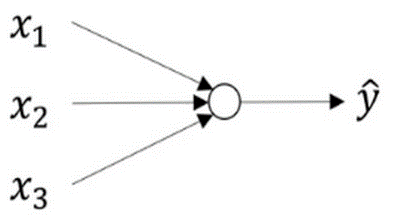
这样的一个模型在神经网络中只是一个节点:

注意, [ i ] 表示第 i 层,( i ) 表示第 i 个训练样本,不能搞混了。
一个神经网络会包含很多层,其实道理跟最简单的逻辑回归模型是一样的,都是从左到右做前向传播,由特征值得到最终结果预测值,训练的话,从右往左依次求导,就可以对参数进行更新。
3.2 神经网络的表示

- 输入层:图中最左侧的输入特征 x1、x2、x3 组成的一层称为输入层,也就是这个神经网络的输入。
- 隐藏层:在神经网络的训练中,我们用到的训练集只包含输入层和输出层的数据,而神经网络中的的数据是看不到的,但是它们又确实存在,于是称之为隐藏层。
- 输出层:在图中,这个神经网络只有一个 y^ 作为输出,它是由一个节点输出的,这个节点就是这个神经网络的输出层。
神经网络中,每一个输入都可以使用带上角标 [ i ] 的 a 来表示,由于上一层的节点被激活后才会有输出,于是这里的 a 表示下一层节点输入的激活值(Active Value)。
在这个示例里,输出层的每个输入特征都可以写成 a ,表示输入层的激活值,其上角标都为 [ 0 ];
在隐藏层,我们可以看到有四个节点,于是就会有四个激活值从节点输出,并输入到下一层,这里的激活值 a 的上角标都为 [ 1 ] ,在代码中,我们把这一层的激活值集合到一个列向量里,如图所示:

最后的输出层产生的数值,也就是 y^,我们将其取值为 上角标为 [ 2 ] 的激活值 a。
在深度学习领域,神经网络的层数是不包含输入层的,于是我们把这个示例称为一个两层的神经网络。
3.3 计算一个神经网络的输出
3.3.1 神经网络的符号惯例
- x :输入特征
- a :每个神经元的输出
- W :特征的权重
- 上标 [ i ] :神经网络的第 i 层
- 下标 i :该层神经网络的第 i 个神经元
3.3.2 神经网络的计算
其实就跟之前提到的逻辑回归是一样的,首先计算 z,再套用 Sigmoid 函数计算出 a,一个神经网络只是这样做了好多次重复计算。

回到前面的示例,我们有了输入后,就可以计算隐藏层的激活值:

在代码中,我们可以利用矩阵运算(向量化)来缩短计算时间:
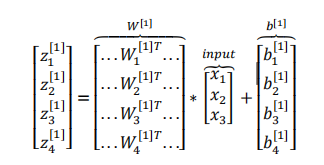
总而言之,在这里我们只要做下面这四个计算:

通过这些公式,我们可以根据给出的一个单独的输入特征向量计算出一个简单神经网络的输出。
3.4 多样本向量化
神经网络训练中涉及到很多输入样本,我们需要把这些输入样本集成到一个矩阵中,这样就可以实现更加方便的计算,通过矩阵运算可以同时对所有样本进行预测值的求解,矩阵如下:

从水平上看,矩阵代表了 m 个训练样本,从竖直上看,矩阵的不同 [ i ] 索引对应了不同的隐藏单元。
3.5 向量化实现的解释
使用上面的方法得到矩阵和向量后就可以使用先前的公式进行 z 的计算了:
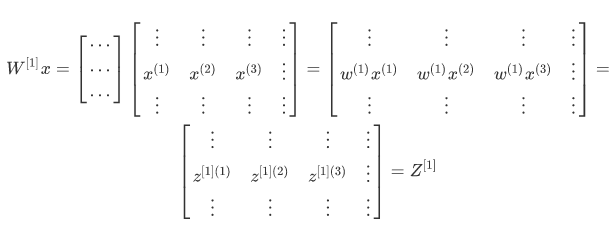
矩阵乘以列向量,最终得到的是列向量,再通过向量和常数的加法,加上 b,也就得到了最终的 z。
3.6 激活函数
训练一个神经网络时,需要决定使用哪种激活函数用在隐藏层上,哪种用在输出层上。激活函数有很多,上面只提到了 Sigmoid 函数,但其实还有其他的,有时候用起来更好。

选择激活函数的经验:
- 对于二分类问题,输出层选择 Sigmoid 函数,然后其他的所有单元都选择 Relu 函数;
- 如果在隐藏层上不确定使用哪个激活函数,那就用 Relu 函数。
要注意的区别:
- 在实践中,使用 Relu 函数激活的神经网络通常比用 sigmoid 或 tanh 函数激活的学习地更快;
- sigmoid 函数和 tanh 函数在正负饱和区的梯度都接近于0,这会造成梯度弥散,而 Relu 函数和 Leaky Relu 函数大于0部分都为常数,不会产生梯度弥散现象。
3.11 随机初始化
我们在训练神经网络的时候,权重随机初始化是很重要的,因为如果所有节点输出的权重值一样的话,同一层下的所有节点将会是一模一样的,那样设置这些节点就没有意义。