深度学习Day-15：LSTM实现火灾预测

news2024/10/6 6:30:23

 🍨 本文为：[🔗365天深度学习训练营] 中的学习记录博客
 🍖 原作者：[K同学啊 | 接辅导、项目定制]

要求：

  1. 了解LSTM是什么，并使用其构建一个完整的程序；
  2. R2达到0.83；

一、 基础配置

  • 语言环境：Python3.7
  • 编译器选择：Pycharm
  • 深度学习环境：TensorFlow2.4.1
  • 数据集：私有数据集

二、 前期准备 

1.设置GPU

import tensorflow as tf

gpus = tf.config.list_physical_devices("GPU")

if gpus:
    tf.config.experimental.set_memory_growth(gpus[0], True)  #设置GPU显存用量按需使用
    tf.config.set_visible_devices([gpus[0]],"GPU")

# 打印显卡信息，确认GPU可用
print(gpus)

根据个人设备情况，选择使用GPU/CPU进行训练，若GPU可用则输出：

[PhysicalDevice(name='/physical_device:GPU:0', device_type='GPU')]

由于在设备上安装的CUDA版本与TensorFlow版本不一致，故这里直接安装了CPU版的TensorFlow，无上述输出。

2. 导入数据

本项目所采用的数据集未收录于公开数据中，故需要自己在文件目录中导入相应数据集合，并设置对应文件目录，以供后续学习过程中使用。

运行下述代码，实现文件写入：

import  pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

df_1 = pd.read_csv("./data/woodpine2.csv")

3.数据可视化 

通过运行下述代码

plt.rcParams['savefig.dpi'] = 500
plt.rcParams['figure.dpi'] = 500

fig,ax = plt.subplots(1,3,constrained_layout = True , figsize = (14,3))

sns.lineplot(data=df_1["Tem1"],ax=ax[0])
sns.lineplot(data=df_1["CO 1"],ax=ax[1])
sns.lineplot(data=df_1["Soot 1"],ax=ax[2])

plt.show()

可以得到如下输出：

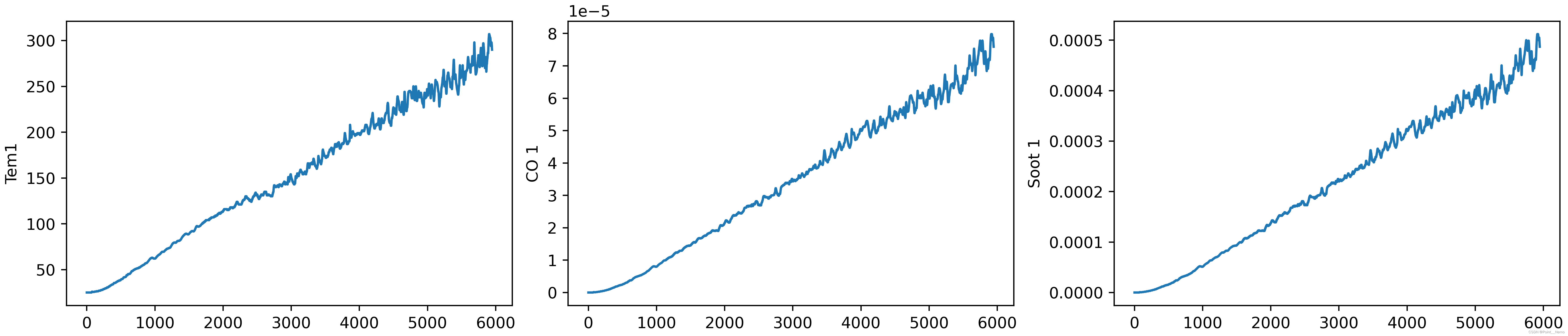
三、数据预处理

1.设置X,y

首先通过下面代码，将数据集一列的时间行去除（即保留第二列值最后一列的所有列），并按照序号的形式排列：

dataFrame = df_1.iloc[:,1:]
print(dataFrame)

得到如下输出：

       Tem1      CO 1    Soot 1
0      25.0  0.000000  0.000000
1      25.0  0.000000  0.000000
2      25.0  0.000000  0.000000
3      25.0  0.000000  0.000000
4      25.0  0.000000  0.000000
...     ...       ...       ...
5943  295.0  0.000077  0.000496
5944  294.0  0.000077  0.000494
5945  292.0  0.000077  0.000491
5946  291.0  0.000076  0.000489
5947  290.0  0.000076  0.000487

[5948 rows x 3 columns]

因为需要实现：使用1-8时刻段预测9时刻段，则通过下述代码做好长度的确定：

width_X = 8
width_y = 1

接着，我们根据刚刚确定的长度，对数据进行划分：

X = []
y = []

in_start = 0

for _,_ in df_1.iterrows():
    in_end = in_start + width_X
    out_end = in_end + width_y

    if out_end < len(dataFrame):
        X_ = np.array(dataFrame.iloc[in_start:in_end,])
        X_ = X_.reshape((len(X_)*3))
        y_ = np.array(dataFrame.iloc[in_end:out_end,0])

        X.append(X_)
        y.append(y_)

    in_start += 1

X = np.array(X)
y = np.array(y)

print(X.shape,y.shape)

得到如下输出： 

(5939, 24) (5939, 1)

2.归一化

from sklearn.preprocessing import MinMaxScaler

sc = MinMaxScaler(feature_range=(0,1))
X_scaled = sc.fit_transform(X)
print(X_scaled.shape)

得到如下输出：

(5939, 24)

通过运行下述代码：

X_scaled = X_scaled.reshape(len(X_scaled),width_X,3)
print(X_scaled.shape)

 得到如下输出：

(5939, 8, 3)

 3.划分数据集

取5000之前的数据作为训练集，5000之后的数据作为验证集：

X_train = np.array(X_scaled[:5000]).astype('float64')
y_train = np.array(y[:5000]).astype('float64')

X_test = np.array(X_scaled[5000:]).astype('float64')
y_test = np.array(y[5000:]).astype('float64')

print(X_train.shape)

得到如下输出：

(5000, 8, 3)

四、构建模型

from tensorflow.keras.models import Sequential
from  tensorflow.keras.layers import Dense,LSTM

model_lstm = Sequential()
model_lstm.add(LSTM(units=64,activation='relu',return_sequences=True,input_shape=(X_train.shape[1],3)))
model_lstm.add(LSTM(units=64,activation='relu'))
model_lstm.add(Dense(width_y))

通过上述代码，构建了一个包含两个LSTM层和一个全连接层的LSTM模型。这个模型将接受形状为 (X_train.shape[1], 3) 的输入，其中 X_train.shape[1] 是时间步数，3 是每个时间步的特征数。

五、 编译模型 

通过下列示例代码：

model_lstm.compile(loss='mean_squared_error',
              optimizer=tf.keras.optimizers.Adam(1e-3))

六、训练模型 

通过下列示例代码：

history = model_lstm.fit(X_train,y_train,
                    epochs = 40,
                    batch_size = 64,
                    validation_data=(X_test,y_test),
                    validation_freq= 1)

运行得到如下输出： 

Epoch 1/40
79/79 [==============================] - 2s 8ms/step - loss: 17138.3194 - val_loss: 387.7700
Epoch 2/40
79/79 [==============================] - 0s 5ms/step - loss: 156.8192 - val_loss: 84.9699
Epoch 3/40
79/79 [==============================] - 0s 5ms/step - loss: 81.8648 - val_loss: 68.5054
Epoch 4/40
79/79 [==============================] - 0s 5ms/step - loss: 68.0213 - val_loss: 59.3978
Epoch 5/40
79/79 [==============================] - 0s 5ms/step - loss: 55.6423 - val_loss: 47.6963
Epoch 6/40
79/79 [==============================] - 0s 5ms/step - loss: 38.9104 - val_loss: 22.8840
Epoch 7/40
79/79 [==============================] - 0s 5ms/step - loss: 20.2978 - val_loss: 17.1035
Epoch 8/40
79/79 [==============================] - 0s 5ms/step - loss: 13.7244 - val_loss: 12.1882
Epoch 9/40
79/79 [==============================] - 0s 5ms/step - loss: 10.3110 - val_loss: 8.4652
Epoch 10/40
79/79 [==============================] - 0s 5ms/step - loss: 7.0844 - val_loss: 7.8640
Epoch 11/40
79/79 [==============================] - 0s 5ms/step - loss: 7.1910 - val_loss: 5.8354
Epoch 12/40
79/79 [==============================] - 0s 5ms/step - loss: 6.7678 - val_loss: 7.7343
Epoch 13/40
79/79 [==============================] - 0s 5ms/step - loss: 6.6999 - val_loss: 5.7382
Epoch 14/40
79/79 [==============================] - 0s 5ms/step - loss: 7.1541 - val_loss: 5.1997
Epoch 15/40
79/79 [==============================] - 0s 5ms/step - loss: 6.5144 - val_loss: 6.5061
Epoch 16/40
79/79 [==============================] - 0s 5ms/step - loss: 7.3389 - val_loss: 5.5619
Epoch 17/40
79/79 [==============================] - 0s 5ms/step - loss: 5.2598 - val_loss: 6.1282
Epoch 18/40
79/79 [==============================] - 0s 5ms/step - loss: 5.5437 - val_loss: 5.1723
Epoch 19/40
79/79 [==============================] - 0s 5ms/step - loss: 5.5292 - val_loss: 5.1508
Epoch 20/40
79/79 [==============================] - 0s 5ms/step - loss: 6.0629 - val_loss: 6.0754
Epoch 21/40
79/79 [==============================] - 0s 5ms/step - loss: 6.0709 - val_loss: 6.4894
Epoch 22/40
79/79 [==============================] - 0s 5ms/step - loss: 6.0648 - val_loss: 21.8828
Epoch 23/40
79/79 [==============================] - 0s 5ms/step - loss: 8.5592 - val_loss: 5.8904
Epoch 24/40
79/79 [==============================] - 0s 5ms/step - loss: 6.3601 - val_loss: 5.2167
Epoch 25/40
79/79 [==============================] - 0s 5ms/step - loss: 5.5161 - val_loss: 9.1012
Epoch 26/40
79/79 [==============================] - 0s 5ms/step - loss: 7.0404 - val_loss: 5.1254
Epoch 27/40
79/79 [==============================] - 0s 5ms/step - loss: 5.1161 - val_loss: 5.8873
Epoch 28/40
79/79 [==============================] - 0s 5ms/step - loss: 5.6961 - val_loss: 5.6163
Epoch 29/40
79/79 [==============================] - 0s 5ms/step - loss: 5.9653 - val_loss: 4.9996
Epoch 30/40
79/79 [==============================] - 0s 5ms/step - loss: 7.2178 - val_loss: 6.9434
Epoch 31/40
79/79 [==============================] - 0s 5ms/step - loss: 6.4113 - val_loss: 24.5538
Epoch 32/40
79/79 [==============================] - 0s 5ms/step - loss: 12.1477 - val_loss: 5.6929
Epoch 33/40
79/79 [==============================] - 0s 5ms/step - loss: 6.0340 - val_loss: 8.0783
Epoch 34/40
79/79 [==============================] - 0s 5ms/step - loss: 8.2311 - val_loss: 6.0748
Epoch 35/40
79/79 [==============================] - 0s 5ms/step - loss: 6.2481 - val_loss: 14.7295
Epoch 36/40
79/79 [==============================] - 0s 5ms/step - loss: 11.7388 - val_loss: 5.4054
Epoch 37/40
79/79 [==============================] - 0s 5ms/step - loss: 5.7323 - val_loss: 6.3847
Epoch 38/40
79/79 [==============================] - 0s 5ms/step - loss: 7.3201 - val_loss: 5.1389
Epoch 39/40
79/79 [==============================] - 0s 5ms/step - loss: 5.7554 - val_loss: 5.1562
Epoch 40/40
79/79 [==============================] - 0s 5ms/step - loss: 5.4301 - val_loss: 5.4044

模型训练结果为：loss大致回归

六、 模型评估

1.Loss与Accuracy图

import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

plt.figure(figsize=(5, 3),dpi=120)

plt.plot(history.history['loss'],label = 'LSTM Training Loss')
plt.plot(history.history['val_loss'],label = 'LSTM Validation Loss')

plt.title('Training and Validation Accuracy')
plt.legend()
plt.show()

得到的可视化结果：

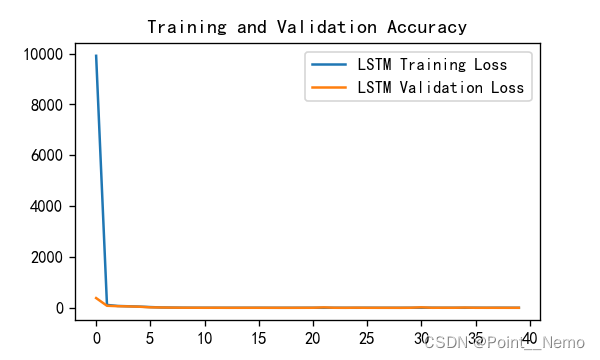
2.调用模型进行预测

通过：

predicted_y_lstm = model_lstm.predict(X_test)

y_tset_one = [i[0] for i in y_test]
predicted_y_lstm_one = [i[0] for i in predicted_y_lstm]

plt.figure(figsize=(5,3),dpi=120)
plt.plot(y_tset_one[:1000],color = 'red', label = '真实值')
plt.plot(predicted_y_lstm_one[:1000],color = 'blue', label = '预测值')

plt.title('Title')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.show()

得到：

3. 查看误差

通过：

from  sklearn import metrics

RMSE_lstm = metrics.mean_squared_error(predicted_y_lstm,y_test)**0.5
R2_lstm = metrics.r2_score(predicted_y_lstm,y_test)

print('均方根误差：%.5f' % RMSE_lstm)
print('R2:%.5f' % R2_lstm)

得到：

均方根误差：2.32473
R2:0.99873

 可见，R2 = 0.99873，优于要求中的 0.83。

七、个人理解

本项目为通过LSTM来实现火灾的预测，需要根据给定的CSV文件来实现该目标。

  1. 本项目中，实现了对表格数据的可视化及异步预测，即通过前一段时刻得到的数据预测后续某一特定时刻的数据情况；
  2. LSTM可以理解为升级版的RNN，传统的RNN中存在着“梯度爆炸”和“短时记忆”的问题，向RNN中加入了遗忘门、输入门及输出门使得困扰RNN的问题得到了一定的解决；
  3. 关于LSTM的实现流程：（1、单输出时间步）单输入单输出、多输入单输出、多输入多输出（2、多输出时间步）单输入单输出、多输入单输出、多输入多输出；
  4. 针对本项目中的拔高要求，目前未能实现；

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1640803.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

小米电脑回收站已清空？别急，恢复数据有妙招

小米电脑回收站已清空？别急，恢复数据有妙招

在数字时代&#xff0c;电脑已经成为我们日常生活和工作中不可或缺的工具。对于小米电脑用户而言&#xff0c;回收站是一个方便我们管理文件的工具&#xff0c;但有时候&#xff0c;误操作或不小心清空回收站可能会让我们面临数据丢失的风险。那么&#xff0c;当小米电脑的回收…
阅读更多...
Linux学习之路 -- 文件 -- 文件操作

Linux学习之路 -- 文件 -- 文件操作

在学习C语言时&#xff0c;我们就学习过文件相关的内容&#xff0c;但是由于知识储备尚且不足&#xff0c;无法深入的了解文件&#xff0c;下面我们就要重新认识一下文件。 <1> 简单介绍(铺垫) 1.前面我们说过&#xff0c;文件 内容 属性&#xff0c;所以我们对文件的…
阅读更多...
ThreeJS:坐标辅助器与轨道控制器

ThreeJS:坐标辅助器与轨道控制器

ThreeJS与右手坐标系 使用ThreeJS创建3D场景时&#xff0c;需要使用一个坐标系来定位和控制对象的位置和方向。 ThreeJS使用的坐标系是右手坐标系&#xff0c;即&#xff1a;X轴向右、Y轴向上、Z轴向前&#xff0c;如下图所示&#xff0c; ThreeJS-右手坐标系 Tips&#xff1a;…
阅读更多...
java技术栈快速复习05_基础运维（linux，git）

java技术栈快速复习05_基础运维（linux，git）

Linux知识总览 linux可以简单的理解成和window一样的操作系统。 Linux和Windows区别 Linux是严格区分大小写的&#xff1b;Linux中一切皆是文件&#xff1b;Linux中文件是没有后缀的&#xff0c;但是他有一些约定俗成的后缀&#xff1b;Windows下的软件一般是无法直接运行的Li…
阅读更多...
JDK14特性

JDK14特性

JDK14 1 概述2 语法层面的变化1_instanceof的模式匹配(预览)2_switch表达式(标准)3_文本块改进(第二次预览)4_Records 记录类型(预览 JEP359) 3 API层面的变化4 关于GC1_G1的NUMA内存分配优化2_弃用SerialCMS,ParNewSerial Old3_删除CMS4_ZGC on macOS and Windows 4 其他变化1…
阅读更多...
《Git---Windows Powershell提交信息中文乱码解决方案》

《Git---Windows Powershell提交信息中文乱码解决方案》

解释&#xff1a; Windows PowerShell中的Git乱码通常是因为字符编码不正确或Git配置不支持Windows系统的默认编码导致的。Git在处理文件时可能使用UTF-8编码&#xff0c;而Windows系统的命令行工具&#xff08;如PowerShell&#xff09;默认使用的是Windows-1252或GBK编码。 …
阅读更多...
Unity Animation--动画剪辑

Unity Animation--动画剪辑

Unity Animation--动画剪辑 动画剪辑 动画剪辑是Unity动画系统的核心元素之一。Unity支持从外部来源导入动画&#xff0c;并提供创建动画剪辑的能力使用“动画”窗口在编辑器中从头开始。 外部来源的动画 从外部来源导入的动画剪辑可能包括&#xff1a; 人形动画 运动捕捉…
阅读更多...
3.4 无关、基和维度

3.4 无关、基和维度

这一节是关于子空间的真实大小。对于 m n m\times n mn 的矩阵&#xff0c;它有 n n n 个列&#xff0c;但是它真正的维数不一定为 n n n&#xff0c;维数可以由无关列的个数来得到。列空间的实际维度就是秩 r r r。 无关的概念是用于向量空间中的任意向量 v 1 , . . . ,…
阅读更多...
C++入门第二节--关键字、命名空间、输入输出

C++入门第二节--关键字、命名空间、输入输出

点赞关注不迷路&#xff01;本节涉及c入门关键字、命名空间、输入输出... 1. C关键字 C总计63个关键字&#xff0c;C语言32个关键字 asmdoifreturntrycontinueautodoubleinlineshorttypedefforbooldynamic_castintsignedtypeidpublicbreakelselongsizeoftypenamethrowcaseen…
阅读更多...
【Java EE】CAS原理和实现以及JUC中常见的类的使用

【Java EE】CAS原理和实现以及JUC中常见的类的使用

˃͈꒵˂͈꒱ write in front ꒰˃͈꒵˂͈꒱ ʕ̯•͡˔•̯᷅ʔ大家好&#xff0c;我是xiaoxie.希望你看完之后,有不足之处请多多谅解&#xff0c;让我们一起共同进步૮₍❀ᴗ͈ . ᴗ͈ აxiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客 本文由xiaoxieʕ̯•͡˔•̯᷅ʔ 原创 CSDN 如…
阅读更多...
OpenCV如何在图像中寻找轮廓(60)

OpenCV如何在图像中寻找轮廓(60)

返回:OpenCV系列文章目录&#xff08;持续更新中......&#xff09; 上一篇&#xff1a;OpenCV如何模板匹配(59) 下一篇 :OpenCV检测凸包(61) 目标 在本教程中&#xff0c;您将学习如何&#xff1a; 使用 OpenCV 函数 cv::findContours使用 OpenCV 函数 cv::d rawContours …
阅读更多...
ROS机器人入门：机器人系统仿真【学习记录】——1

ROS机器人入门：机器人系统仿真【学习记录】——1

最近闲来无事&#xff0c;重温了一下ROS方面的相关知识。先前的学习都是一带而过&#xff0c;发现差不多都忘了&#xff0c;学习的不够深入。因此&#xff0c;在重温的同时&#xff0c;于先前写下了2篇ROS架构与通信机制的博客&#xff1a; 对应的博客的链接为&#xff1a; R…
阅读更多...
【副本向】高等级副本全流程开发

【副本向】高等级副本全流程开发

副本的创建 1.从配置表通过副本ID获取此副本参数 Tab_CopyScene rCopyScene TableManager.GetCopySceneByID(m_CopySceneID);if (rCopyScene ! null){//只要配置了组队的Rule&#xff0c;就是组队模式&#xff0c;否则就是单人模式bool bSolo true;for (int n 0; n < rCo…
阅读更多...
菜鸡学习netty源码（三）—— Reactor 模型

菜鸡学习netty源码（三）—— Reactor 模型

1.概述 我们先进行理解一下Reactor模型&#xff0c;知道什么是Reactor模型&#xff0c;它有什么特别之处。我们先来简单介绍一下这个Reactor模型。 Reactor模型的核心思想&#xff1a; 就是将所关注的I/O事件进行注册到一个多路复用器上&#xff0c;一旦有I/O事件的发生&#…
阅读更多...
Debian 12 -bash: netstat: command not found 解决办法

Debian 12 -bash: netstat: command not found 解决办法

问题表现&#xff1a; debian 12系统中&#xff0c;不能使用 netstat命令 处理办法&#xff1a; netstat 命令就的net-tools中&#xff0c;把net-tools工具安装上就好了。 apt-get install netstat 安装之后就可以使用netstat 命令了&#xff0c;如查询端口情况&#xff1a; …
阅读更多...
快速排序的单趟排序方法对比

快速排序的单趟排序方法对比

这里的霍尔法内容来自文章&#xff1a;【排序算法】快速排序&#xff08;C语言&#xff09;_c语言快速排序-CSDN博客 霍尔法 单趟排序使用霍尔法&#xff0c;这样的话我们必须保证除了指针停留的位置到头之外&#xff0c;最后首尾指针共同指向的是一个比key小的值&#xff0c…
阅读更多...
启动盘制作

启动盘制作

魔术师pe安装教程 我一般使用魔术师来安装windows系统 魔术师pe地址下载 解压后使用 把ios映像文件放入pe系统u盘下 开机按f1,进入bios,将usb接口拉到本电脑&#xff0c;在按f10保存&#xff0c;在按f12即可找到pe的u盘 ventoy安装教程 其他系统安装我使用ventoy ventoy地…
阅读更多...
一个5000刀的XSS

一个5000刀的XSS

背景介绍 今天分享国外一个白帽小哥Crypto通过发现Apple某网站XSS而获得5000美元赏金的故事。废话不多说&#xff0c;让我们开始吧&#xff5e; 狩猎过程 易受攻击的 Apple 服务网站是&#xff1a;https://discussions.apple.com&#xff0c;该服务是苹果用户和开发者讨论问题…
阅读更多...
【笔记】Simulink与Workbench交互+自定义m函数封装为Simulink模块

【笔记】Simulink与Workbench交互+自定义m函数封装为Simulink模块

以如下三角函数为例&#xff0c;说明建模方法 ya*sin(b*2*pi*uc);0.总模型总代码 总模型 总代码&#xff1a; clc clear close allt_all10; a10; b1; c0;%pi/2; delta_t0.01; simOutsim(test240430); out_tsimOut.tout; out_y1simOut.yout{1}.Values; out_y2simOut.yout{2}.…
阅读更多...
栈的磁盘优化：降低存取成本的算法与实现

栈的磁盘优化：降低存取成本的算法与实现

栈的磁盘优化&#xff1a;降低存取成本的算法与实现 问题背景简单实现方法的分析实现方法PUSH操作POP操作成本分析渐近分析 优化实现方法实现方法成本分析渐近分析 进一步优化&#xff1a;双页管理策略实现方法管理策略成本分析 伪代码示例C代码示例结论 问题背景 在具有有限快…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023