一、引入

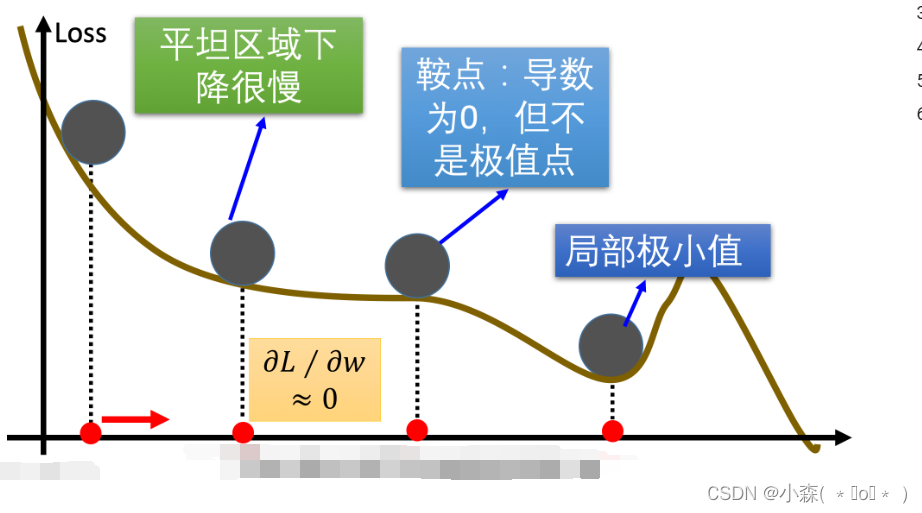
在传统的梯度下降优化算法中，如果碰到平缓区域，梯度值较小，参数优化变慢 ，遇到鞍点（是指在某些方向上梯度为零而在其他方向上梯度非零的点。），梯度为 0，参数无法优化，碰到局部最小值。实践中使用的小批量梯度下降法（mini-batch SGD）因其梯度估计的噪声性质，有时能够使模型脱离这些点。

💥为了克服这些困难，研究者们提出了多种改进策略，出现了一些对梯度下降算法的优化方法：Momentum、AdaGrad、RMSprop、Adam 等。

二、指数加权平均

我们最常见的算数平均指的是将所有数加起来除以数的个数，每个数的权重是相同的。加权平均指的是给每个数赋予不同的权重求得平均数。指数加权平均是一种数据处理方式，它通过对历史数据应用不同的权重来减少过去数据的影响，并强调近期数据的重要性。

[ vt = beta * v{t-1} + (1 - beta) * theta_t] 

比如：明天气温怎么样，和昨天气温有很大关系，而和一周前的气温关系就小一些。 

vt​ 是第 𝑡 天的平均温度值，𝜃𝑡​ 是第 𝑡t 天的实际观察值，而 𝛽 是一个可调节的超参数（通常 0<𝛽<1）。这个公式表明，当前的平均值是前一天平均值与当天实际值的加权平均。

• β 调节权重系数，该值越大平均数越平缓。

 我们接下来通过一段代码来看下结果，随机产生进 30 天的气温数据：

import torch
import matplotlib.pyplot as plt
import os
os.environ['KMP_DUPLICATE_LIB_OK']='TRUE'


# 实际平均温度
def test01():

    # 固定随机数种子
    torch.manual_seed(0)

    # 产生30天的随机温度
    temperature = torch.randn(size=[30]) * 10
    print(temperature)

    # 绘制平均温度
    days = torch.arange(1, 31, 1)
    plt.plot(days, temperature, color='r')
    plt.scatter(days, temperature)
    plt.show()

# 指数加权平均温度
def test02(beta=0.8):

    # 固定随机数种子
    torch.manual_seed(0)
    # torch.initial_seed()
    # 产生30天的随机温度
    temperature = torch.randn(size=[30,]) * 10
    print(temperature)

    exp_weight_avg = []
    for idx, temp in enumerate(temperature, 1):

        # 第一个元素的的 EWA 值等于自身
        if idx == 1:
            exp_weight_avg.append(temp)
            continue

        # 第二个元素的 EWA 值等于上一个 EWA 乘以 β + 当前气氛乘以 (1-β)
        new_temp = exp_weight_avg[idx - 2] * beta + (1 - beta) * temp
        exp_weight_avg.append(new_temp)


    days = torch.arange(1, 31, 1)
    plt.plot(days, exp_weight_avg, color='r')
    plt.scatter(days, temperature)
    plt.show()


if __name__ == '__main__':

    test01()
    test02()

这是test01执行后产生的实际值： 

 我们再看一下指数平均后的值：

🔎指数加权平均绘制出的气氛变化曲线更加平缓; β 的值越大，则绘制出的折线越加平缓； 

三、Momentum

我们通过对指数加权平均的知识来研究Momentum优化方法💢

• 鞍点：梯度为零的点，损失函数的梯度在所有方向上都接近或等于零。由于梯度为零，标准梯度下降法在此将无法继续优化参数。
• 平缓区域：这些区域的梯度值较小，导致参数更新缓慢。虽然这意味着算法接近极小值点，但收敛速度会变得非常慢。

当梯度下降碰到 “峡谷” 、”平缓”、”鞍点” 区域时，参数更新速度变慢，Momentum 通过指数加权平均法，累计历史梯度值，进行参数更新，越近的梯度值对当前参数更新的重要性越大。

Momentum优化方法是对传统梯度下降法的一种改进：

Momentum优化算法的核心思想是在一定程度上积累之前的梯度信息，以此来调整当前的梯度更新方向。这种方法可以在一定程度上减少训练过程中的摆动现象，使得学习过程更加平滑，从而可能使用较大的学习率而不必担心偏离最小值太远。 

梯度计算公式：Dt = β * St-1 + (1- β) * Dt

在面对梯度消失、鞍点等问题时，Momentum能够改善SGD的表现，帮助模型跳出局部最小值或平坦区域；如果当处于鞍点位置时，由于当前的梯度为 0，参数无法更新。但是 Momentum梯度下降算法已经在先前积累了一些梯度值，很有可能使得跨过鞍点。

由于 mini-batch 普通的梯度下降算法，每次选取少数的样本梯度确定前进方向，可能会出现震荡，使得训练时间变长。Momentum 使用移动加权平均，平滑了梯度的变化，使得前进方向更加平缓，有利于加快训练过程。一定程度上有利于降低 “峡谷” 问题的影响。

Momentum方法的实现案例： 

import torch
import torch.nn as nn
import torch.optim as optim

# 定义模型
model = nn.Linear(10, 1)

# 定义损失函数
criterion = nn.MSELoss()

# 定义优化器，并设置momentum参数为0.9
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)

# 模拟数据
inputs = torch.randn(100, 10)
targets = torch.randn(100, 1)

# 训练模型
for epoch in range(10):
    # 前向传播
    outputs = model(inputs)
    loss = criterion(outputs, targets)

    # 反向传播和优化
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    print('Epoch [{}/{}], Loss: {:.4f}'.format(epoch+1, 10, loss.item()))

Momentum 算法可以理解为是对梯度值的一种调整，我们知道梯度下降算法中还有一个很重要的学习率，Momentum 并没有学习率进行优化。 

四、AdaGrad

💥Momentum 算法是对梯度值调整，使得模型可以更好的进行参数更新，AdaGrad算法则是对学习率，即每次更新走的步长，进行调整更新~

AdaGrad 通过对不同的参数分量使用不同的学习率，AdaGrad 的学习率总体会逐渐减小，这是因为 AdaGrad算法认为：在起初时，我们距离最优目标仍较远，可以使用较大的学习率，加快训练速度，随着迭代次数的增加，学习率逐渐下降。

🗨️计算步骤如下：

1. 初始化学习率 α、初始化参数 θ、小常数 σ = 1e-6
2. 初始化梯度累积变量 s = 0
3. 从训练集中采样 m 个样本的小批量，计算梯度 g
4. 累积平方梯度 s = s + g ⊙ g，⊙ 表示各个分量相乘

 

AdaGrad通过这种方式实现了对每个参数的个性化学习率调整，使得在参数空间较平缓的方向上可以取得更大的进步，而在陡峭的方向上则能够变得更加平缓，从而加快了训练速度( 如果累计梯度值s大的话，学习率就会小一点)        

使用Python实现AdaGrad算法的API代码：

import torch

class AdaGrad:
    def __init__(self, params, lr=0.01, epsilon=1e-8):
        self.params = list(params)
        self.lr = lr
        self.epsilon = epsilon
        self.cache = [torch.zeros_like(param) for param in self.params]

    def step(self):
        for i, param in enumerate(self.params):
            self.cache[i] += param.grad.data ** 2
            param.data -= self.lr * param.grad.data / (torch.sqrt(self.cache[i]) + self.epsilon)

💥AdaGrad 缺点是可能会使得学习率过早、过量的降低，导致模型训练后期学习率太小，较难找到最优解。

五、RMSProp

RMSProp（Root Mean Square Prop）是一种常用的自适应学习率优化算法，是对 AdaGrad 的优化，最主要的不同是，RMSProp使用指数移动加权平均梯度替换历史梯度的平方和。

1. 初始化学习率 α、初始化参数 θ、小常数 σ = 1e-6
2. 初始化参数 θ
3. 初始化梯度累计变量 s
4. 从训练集中采样 m 个样本的小批量，计算梯度 g
5. 使用指数移动平均累积历史梯度

 

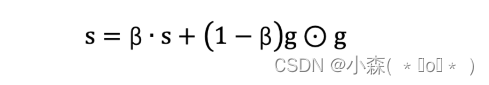
RMSProp 与 AdaGrad 最大的区别是对梯度的累积方式不同，对于每个梯度分量仍然使用不同的学习率。RMSProp 通过引入衰减系数 β，控制历史梯度对历史梯度信息获取的多少，使得学习率衰减更加合理一些。 

import numpy as np

def rmsprop(params, grads, learning_rate=0.01, decay_rate=0.9, epsilon=1e-8):
    cache = {}
    for key in params.keys():
        cache[key] = np.zeros_like(params[key])

    for key in params.keys():
        cache[key] = decay_rate * cache[key] + (1 - decay_rate) * grads[key] ** 2
        params[key] -= learning_rate * grads[key] / (np.sqrt(cache[key]) + epsilon)

    return params

params是一个字典，包含了模型的参数；grads是一个字典，包含了参数对应的梯度；learning_rate是学习率；decay_rate是衰减系数；epsilon是一个很小的正数，用于防止除以零。

六、Adam 

💯Adam 结合了两种优化算法的优点：RMSProp（Root Mean Square Prop）和Momentum。Adam在深度学习中被广泛使用，因为它能够自动调整学习率，特别适合处理大规模数据集和复杂模型。

Adam的关键特点：

1. 一阶矩估计（First Moment）：梯度的均值，类似于Momentum中的velocity term，用于指示梯度在何时变得非常剧烈。

2. 二阶矩估计（Second Moment）：梯度的未中心化方差，类似于RMSProp中的平方梯度的指数移动平均值，用于指示梯度变化的范围。

我们在平时使用中会经常用到次方法，在PyTorch中就是optim.Adam方法，不再是optim.SGD方法：

import torch
import torch.nn as nn
import torch.optim as optim

# 定义一个简单的线性模型
class SimpleModel(nn.Module):
    def __init__(self):
        super(SimpleModel, self).__init__()
        self.linear = nn.Linear(10, 1)  # 假设输入维度是10，输出维度是1

    def forward(self, x):
        return self.linear(x)

# 创建模型实例
model = SimpleModel()

# 定义损失函数
criterion = nn.MSELoss()  # 均方误差损失函数

# 创建优化器，设定学习率为0.001，参数beta1默认为0.9，beta2默认为0.999
optimizer = optim.Adam(model.parameters(), lr=0.001)

# 假设有一个输入数据x和对应的目标y
x = torch.randn(32, 10)  # 批量大小为32，每个样本的输入维度是10
y = torch.randn(32, 1)   # 批量大小为32，每个样本的输出维度是1

# 前向传播
outputs = model(x)

# 计算损失
loss = criterion(outputs, y)

# 清空之前所有的梯度
optimizer.zero_grad()

# 反向传播
loss.backward()

# 更新模型参数
optimizer.step()

# 打印损失值
print("Loss: ", loss.item())