文章目录
- Co-assistant Networks for Label Correction
- 摘要
- 方法
- Noise Detector
- Noise Cleaner
- 损失函数
- 实验结果
Co-assistant Networks for Label Correction
摘要
-
问题描述:
- 描述医学图像数据集中存在损坏标签的问题。
- 强调损坏标签对深度神经网络性能的影响。
-
提出方法:
- 引入Co-assistant Networks for Label Correction (CNLC)框架。
- 描述框架的两个模块:噪声检测器和噪声清洗器。
- 解释噪声检测器和噪声清洗器的功能。
-
优化算法设计:
- 描述新的双层优化算法,用于优化提出的目标函数。
-
实验设计:
- 描述实验中使用的三个流行医学图像数据集。
- 说明实验的设置和评估标准。
-
实验结果:
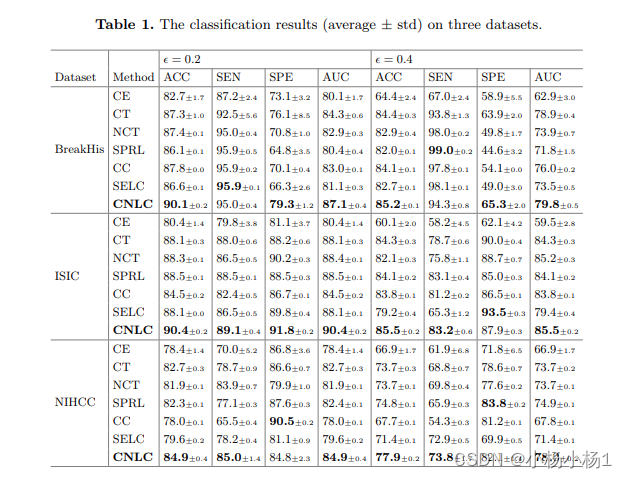
- 展示对比实验结果,证明CNLC框架相对于最先进方法的优越性能。
代码地址
方法
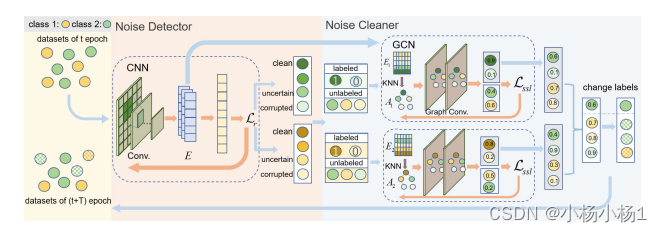
Fig. 1: 所提出的CNLC框架的架构包括两个模块,即噪声检测器和噪声清洗器。噪声检测器输出所有训练样本的嵌入,并将每个类别的训练样本分为三个子组,包括干净样本、不确定样本和损坏样本。噪声清洗器为每个类别构建一个GCN,用于纠正所有类别的损坏样本和一部分不确定样本的标签。
Noise Detector
目前的检测方法设计损失较小的样本被视为干净样本,而损失较大的样本被视为损坏样本。
本文噪声检测器包括两个步骤,即CNN和标签划分,将每个类别的所有训练样本划分为三个子组,即干净样本、不确定样本和损坏样本
首先采用带有交叉熵损失的CNN作为骨干网络来获得所有训练样本的损失。由于交叉熵损失在没有额外抗噪声项的情况下很容易对损坏标签进行过度拟合,将其改为以下抗噪声损失:
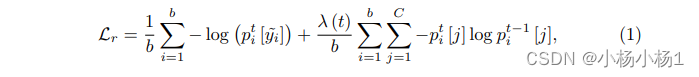
b
b
b 是每个批次中的样本数量,
p
i
t
[
j
]
p^t_{i}[j]
pit[j] 表示第
t
t
t个时期中第
i
i
i 个样本的第
j
j
j 类预测,
y
~
i
∈
{
0
,
1
,
.
.
.
,
C
−
1
}
\tilde{y}_i \in \{0, 1, ..., C - 1\}
y~i∈{0,1,...,C−1} 表示第
i
i
i 个样本
x
i
x_i
xi 的损坏标签,
C
C
C 表示类别数,
λ
(
t
)
\lambda(t)
λ(t) 是与时间相关的超参数。在公式(1)中,第一项是交叉熵损失。第二项是抗噪声损失,旨在平滑模型参数的更新,从而在一定程度上防止模型对损坏标签过度拟合。
Noise Cleaner

噪声清洗器旨在纠正具有损坏标签的样本的标签。目前的方法通常使用深度神经网络(如CNN和MLP)来进行标签纠正,但存在两个问题:一是忽略了样本之间的关系,二是样本数量有限。为了解决这些问题,该研究采用了半监督学习方法,为每个类别使用一个GCN来保持样本的局部拓扑结构,并包括三个组件:噪声率估计、基于类别的GCNs和损坏标签修正。
每个基于类别的GCN的输入包括标记样本和未标记样本。标记样本包括正样本(即该类别的干净样本,标签为新标签
z
i
c
=
1
z_{ic} = 1
zic=1和负样本(即该类别的损坏样本,标签为新标签
z
i
c
=
0
z_{ic} = 0
zic=0)。
未标记样本包括来自所有类别的不确定样本子集和其他类别的损坏样本。我们遵循一个原则来为每个类别选择不确定样本,即在公式(1)中损失越高,样本属于损坏样本的概率越高。此外,不确定样本的数量由噪声率估计确定。在噪声率估计中,使用由两个高斯模型组成的高斯混合模型(GMM)来估计训练样本的噪声率。
如图2所示,损坏样本的高斯模型的均值大于干净样本的高斯模型的均值。因此,均值较大的高斯模型可能是损坏标签的曲线。基于此,给定GMM模型对于第 i 个样本的两个输出,分别为具有较大均值和较小均值的输出,分别表示为
M
i
,
1
M_{i,1}
Mi,1 和
M
i
,
2
M_{i,2}
Mi,2,因此以下定义
v
i
v_i
vi 用于确定第 i 个样本是否为噪声:
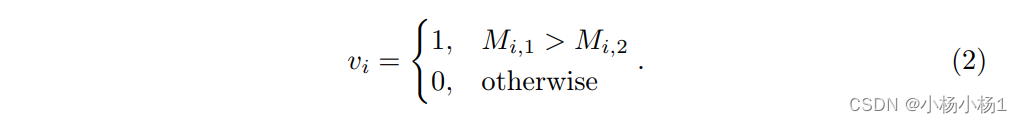
训练样本的噪声率
r
r
r 计算公式为:
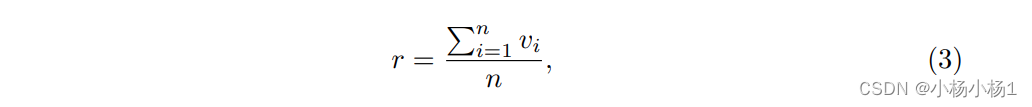
n n n 代表训练数据集中样本的总数。假设第 c c c 类中样本的数量为 s c s_c sc,每个类别的不确定样本数量为 s c × r − n 1 s_c \times r - n_1 sc×r−n1。因此,噪声清洗器中每个类别的未标记样本总数为 n × r − n 1 n \times r - n_1 n×r−n1。
给定 2 × n 1 2 \times n_1 2×n1 个标记样本和 n × r − n 1 n \times r - n_1 n×r−n1 个未标记样本,每个类别的基于类别的GCN进行半监督学习,以预测 n × r n \times r n×r个样本,包括 n × r − n 1 n \times r - n_1 n×r−n1 个未标记样本和 n 1 n_1 n1 个此类别的损坏样本。半监督损失 L ssl L_{\text{ssl}} Lssl 包括用于标记样本的二元交叉熵损失 L bce L_{\text{bce}} Lbce 和用于未标记样本的无监督损失 L mse L_{\text{mse}} Lmse,即 L ssl = L bce + L mse L_{\text{ssl}} = L_{\text{bce}} + L_{\text{mse}} Lssl=Lbce+Lmse
其中
L
bce
L_{\text{bce}}
Lbce 和
L
mse
L_{\text{mse}}
Lmse 定义为:
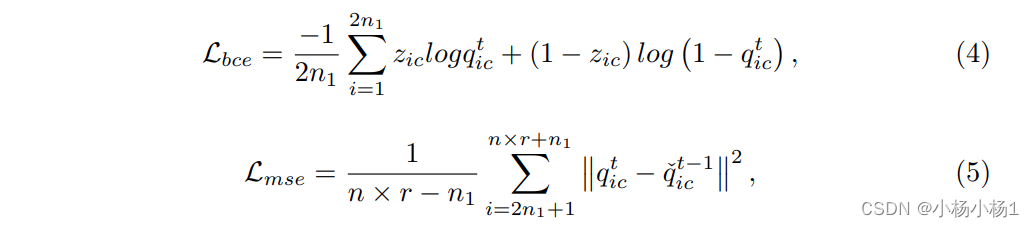
q
i
c
t
q^t_{ic}
qict表示第
t
t
t个时期中第
i
i
i个样本对于类
c
c
c的预测。
在损坏的标签校正中,给定C的GCN以及不确定样本子集和所有损坏样本的每个类的相似性分数,它们的标签可以通过以下方式确定:
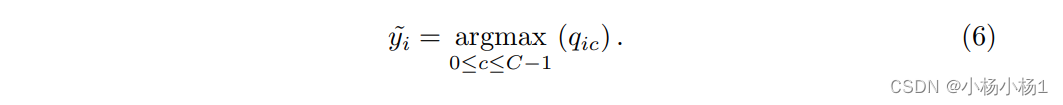
损失函数
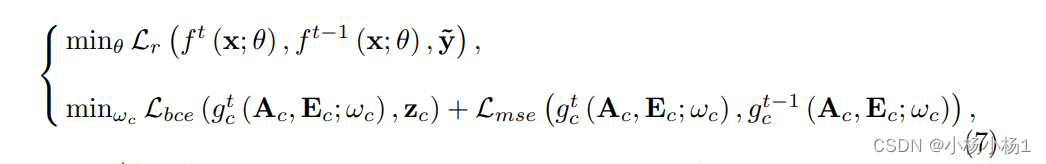
实验结果