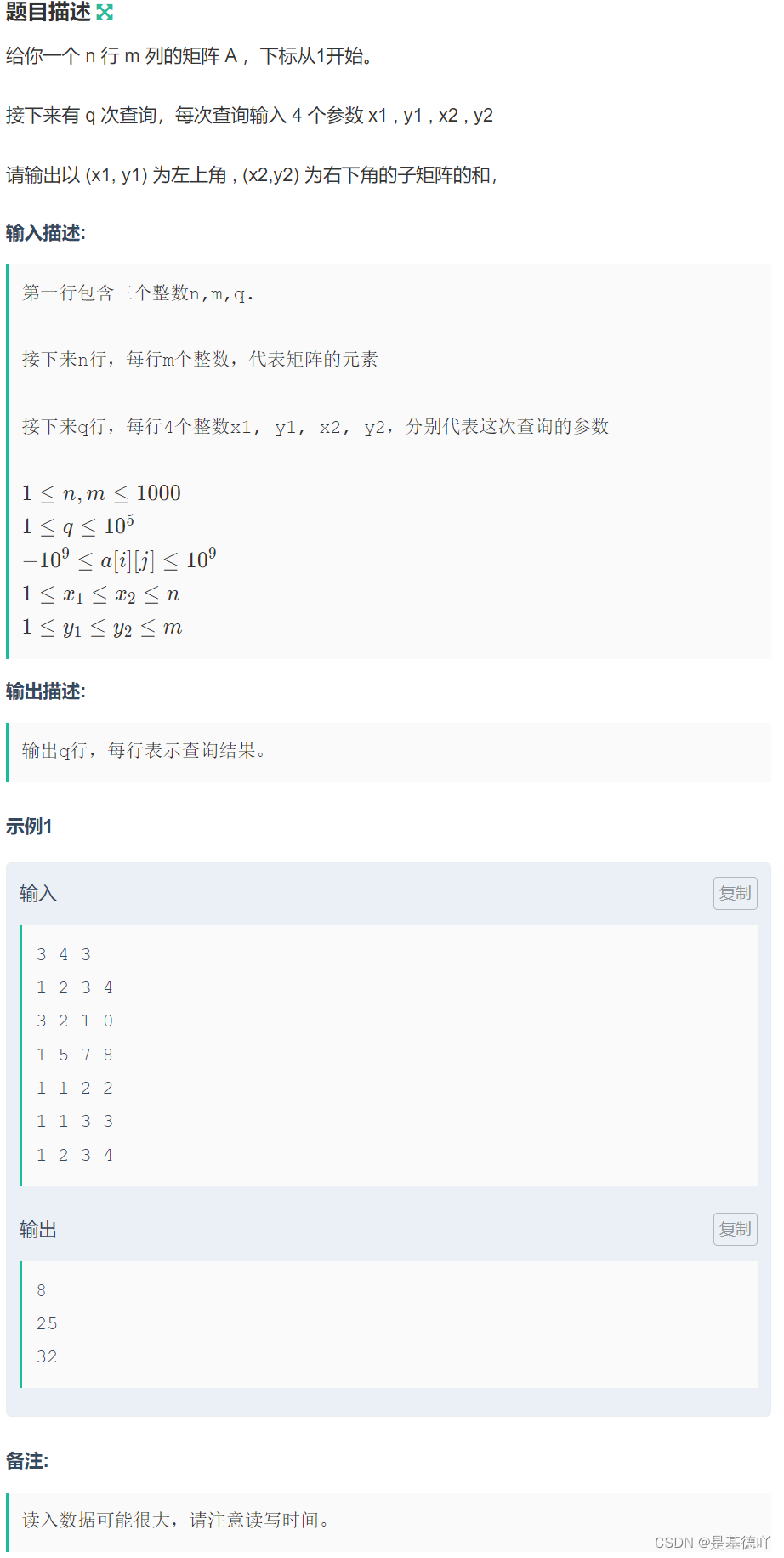
303. 区域和检索 - 数组不可变 - 力扣(LeetCode)
动态规划~
前缀和
最朴素的思想是存储数组nums的值,每次调用sumRange时,通过循环的方法计算数组nums从下标i到下标j的元素和,需要计算j-i+1个元素的和。由于每次检索的时间和检索的下标范围有关,因此检索的时间复杂度较高,如果检索的次数过多,会超出时间限制。
我们应该尽量降低sumRange的时间复杂度,最理想的时间复杂度是O(1)。

因此,要计算sumRange(i,j),则需要计算数组nums在下标i-1和j的前缀和,并计算两个前缀和的差。如果可以在初始化时就计算nums在每个下标的前缀和。即可满足调用sumRange的时间复杂度都是O(1)。
具体实现方面,假设数组的长度nums等于n,创建长度为n+1的前缀和数组nums,sums[i+1]=sums[i]+nums[i],则sums[i]表示数组从0到下标i-1的前缀和。
将前缀和数组 sum 的长度设为 n+1的目的是为了方便计算 sumRange(i,j),不需要对 i=0的情况特殊处理。此时有:
typedef struct {
int* sums;
} NumArray;
NumArray* numArrayCreate(int* nums, int numsSize) {
NumArray* ret=malloc(sizeof(NumArray));
ret->sums=malloc(sizeof(int)*(numsSize+1));
ret->sums[0]=0;
for(int i=0;i<numsSize;i++)
{
ret->sums[i+1]=ret->sums[i]+nums[i];
}
return ret;
}
int numArraySumRange(NumArray* obj, int i, int j) {
return obj->sums[j+1]-obj->sums[i];
}
void numArrayFree(NumArray* obj) {
free(obj->sums);
}
/**
* Your NumArray struct will be instantiated and called as such:
* NumArray* obj = numArrayCreate(nums, numsSize);
* int param_1 = numArraySumRange(obj, left, right);
* numArrayFree(obj);
*/