Codeforces Round 942 (Div. 2) ----- A ----- F --- 题解

news2024/11/17 14:25:49

前情提要：因为数学水平原因，没法给出e的证明，因为我也是举例归类得出的结论，但是按理来说应该可以利用生成数函数证明

f题也是因为数学原因加上水平有限，我的理解可能有偏差。

目录

A. Contest Proposal：

题目大意：

思路解析：

代码实现：

 B. Coin Games：

题目大意：

思路解析：

代码实现：

C. Permutation Counting：

题目大意：

思路解析：

代码实现：

D1. Reverse Card (Easy Version)：

题目大意：

思路解析：

代码实现：

D2. Reverse Card (Hard Version)：

题目大意：

思路解析：

代码实现：

E. Fenwick Tree：

题目大意：

思路解析：

 代码实现：

F. Long Way to be Non-decreasing：

题目大意：

思路解析：

代码实现：

A. Contest Proposal：

题目大意：

思路解析：

现在求使得对于所有i中，ai<=bi，最少需要插入几个新的问题，这里一眼贪心即可。

代码实现：

import java.util.*;


import java.io.*;

public class Main {

    public static void main(String[] args) throws IOException {

        int t = f.nextInt();
        while (t > 0) {
            solve();
            t--;
        }
        w.flush();
        w.close();
    }

    static int mod = 998244353;
    static long inf = (long) 1e18;


    public static void solve() throws IOException {
        int n = f.nextInt();
        int[] a = new int[n];
        int[] b= new int[n];
        for (int i = 0; i < n; i++) {
            a[i] = f.nextInt();
        }
        for (int i = 0; i < n; i++) {
            b[i] = f.nextInt();
        }
        int p = 0;
        int ans = 0;
        for (int i = 0; i < n; i++) {
            if (a[p] <= b[i]){
                p++;
            }else {
                ans++;
            }
        }
        w.println(ans);
    }


    public static void swap(int[] a, int i, int j) {
        int tmp = a[i];
        a[i] = a[j];
        a[j] = tmp;
    }


    public static long qkm(long a, long b, long mod) {
        long res = 1;
        while (b > 0) {
            if ((b & 1) == 1) res = res * a % mod;
            a = a * a % mod;
            b >>= 1;
        }
        return res;
    }

    public static class Pair {
        long x, y;
        int val;

        public Pair(long ne, long val, int x) {
            this.x = ne;
            this.y = val;
            this.val = x;
        }

        @Override
        public boolean equals(Object o) {
            if (this == o) return true;
            if (o == null || getClass() != o.getClass()) return false;
            Pair pair = (Pair) o;
            return x == pair.x && y == pair.y && val == pair.val;
        }

        @Override
        public int hashCode() {
            return Objects.hash(x, y, val);
        }
    }

    public static class Node {
        int x, y, val;

        public Node(int x, int y, int val) {
            this.x = x;
            this.y = y;
            this.val = val;
        }
        public Node(int x, int y) {
            this.x = x;
            this.y = y;
        }

    }


    static PrintWriter w = new PrintWriter(new OutputStreamWriter(System.out));
    static Input f = new Input(System.in);

    static class Input {
        public BufferedReader reader;
        public StringTokenizer tokenizer;

        public Input(InputStream stream) {
            reader = new BufferedReader(new InputStreamReader(stream), 32768);
            tokenizer = null;
        }

        public String next() throws IOException {

            while (tokenizer == null || !tokenizer.hasMoreTokens()) {
                tokenizer = new StringTokenizer(reader.readLine());
            }
            return tokenizer.nextToken();
        }

        public String nextLine() throws IOException {
            String str = null;
            str = reader.readLine();
            return str;
        }

        public int nextInt() throws IOException {
            return Integer.parseInt(next());
        }

        public long nextLong() throws IOException {
            return Long.parseLong(next());
        }

        public Double nextDouble() throws IOException {
            return Double.parseDouble(next());
        }
    }
}

 B. Coin Games：

题目大意：

思路解析：

考虑所有可能的操作：

  • ...UUU...->...DD......：U 的个数减少 3 。
  • ...UUD...->...DU...：U 的数量减少 1 。
  • ...DUU...->...UD...：U 的数量减少 1 。
  • ...DUD... -> ...UU...：U 的数量增加 1 

当U的个数为0时，当前棋手输，可以发现对于所有可能的操作，任意一种情况都会改变U的个数的奇偶性，那么可以得出结论，当初始情况U的个数为奇数时，Alice将赢得游戏。

代码实现：


import java.util.*;


import java.io.*;

public class Main {

    public static void main(String[] args) throws IOException {

        int t = f.nextInt();
        while (t > 0) {
            solve();
            t--;
        }
        w.flush();
        w.close();
    }

    static int mod = 998244353;
    static long inf = (long) 1e18;


    public static void solve() throws IOException {
        int n = f.nextInt();
        char[] s = f.next().toCharArray();
        int cnt = 0;
        for (int i = 0; i < n; i++) {
            if (s[i] == 'U') cnt ^= 1;
        }
        if (cnt == 1) w.println("YES");
        else w.println("NO");
    }


    public static void swap(int[] a, int i, int j) {
        int tmp = a[i];
        a[i] = a[j];
        a[j] = tmp;
    }


    public static long qkm(long a, long b, long mod) {
        long res = 1;
        while (b > 0) {
            if ((b & 1) == 1) res = res * a % mod;
            a = a * a % mod;
            b >>= 1;
        }
        return res;
    }

    public static class Pair {
        long x, y;
        int val;

        public Pair(long ne, long val, int x) {
            this.x = ne;
            this.y = val;
            this.val = x;
        }

        @Override
        public boolean equals(Object o) {
            if (this == o) return true;
            if (o == null || getClass() != o.getClass()) return false;
            Pair pair = (Pair) o;
            return x == pair.x && y == pair.y && val == pair.val;
        }

        @Override
        public int hashCode() {
            return Objects.hash(x, y, val);
        }
    }

    public static class Node {
        int x, y, val;

        public Node(int x, int y, int val) {
            this.x = x;
            this.y = y;
            this.val = val;
        }
        public Node(int x, int y) {
            this.x = x;
            this.y = y;
        }

    }


    static PrintWriter w = new PrintWriter(new OutputStreamWriter(System.out));
    static Input f = new Input(System.in);

    static class Input {
        public BufferedReader reader;
        public StringTokenizer tokenizer;

        public Input(InputStream stream) {
            reader = new BufferedReader(new InputStreamReader(stream), 32768);
            tokenizer = null;
        }

        public String next() throws IOException {

            while (tokenizer == null || !tokenizer.hasMoreTokens()) {
                tokenizer = new StringTokenizer(reader.readLine());
            }
            return tokenizer.nextToken();
        }

        public String nextLine() throws IOException {
            String str = null;
            str = reader.readLine();
            return str;
        }

        public int nextInt() throws IOException {
            return Integer.parseInt(next());
        }

        public long nextLong() throws IOException {
            return Long.parseLong(next());
        }

        public Double nextDouble() throws IOException {
            return Double.parseDouble(next());
        }
    }
}

C. Permutation Counting：

题目大意：

 

思路解析：

这里可以发现能组成排列数的个数肯定与1-n中最少的那个数字相等。

假如 1的个数为3  2的个数为2  3的个数为3，那么肯定可以组成 1 2 3 1 2 3此时排列数为4，1 2 3两个2 3 1一个3 1 2一个，那么我们想剩下的1 和 3是否能再组成新的排列数，答案是可以的，

1 3 2 1 3 2 1 3此时 1 3 2 两个 3 2 1两个 2 1 3两个，此时已经最优了，

那么可以发现答案等于 min + （min-1）*（n-1）+ min（n-1，more+k），k可以提高min的大小

代码实现：


import java.util.*;


import java.io.*;

public class Main {

    public static void main(String[] args) throws IOException {

        int t = f.nextInt();
        while (t > 0) {
            solve();
            t--;
        }
        w.flush();
        w.close();
    }

    static int mod = 998244353;
    static long inf = (long) 1e18;


    public static void solve() throws IOException {
        int n = f.nextInt(); long k = f.nextLong();
        long[] a = new long[n];
        for (int i = 0; i < n; i++) {
            a[i] = f.nextLong();
        }
        int j = 1;

        Arrays.sort(a);
        long min = a[0];
        while (true){
            if (k < j) break;
            if (j < n){
                if ((a[j] - min) * j > k){
                    min += k / j;
                    k %= j;
                    break;
                }else {
                    k -= (a[j] - min) * j;
                    min = a[j];
                    j++;
                }
            }else {
                min += k / j;
                k %= j;
                break;
            }
        }
        if (j == n){
            long ans = min + (min - 1) * (n - 1) + k;
            w.println(ans);
        }else {
            int cnt = 0;
            for (int i = j; i < n; i++) {
                if (a[i] > min) cnt++;
            }
            long ans = min + (min - 1) * (n - 1) + Math.min(n - 1, cnt + k);
            w.println(ans);
        }
    }


    public static void swap(int[] a, int i, int j) {
        int tmp = a[i];
        a[i] = a[j];
        a[j] = tmp;
    }


    public static long qkm(long a, long b, long mod) {
        long res = 1;
        while (b > 0) {
            if ((b & 1) == 1) res = res * a % mod;
            a = a * a % mod;
            b >>= 1;
        }
        return res;
    }

    public static class Pair {
        long x, y;
        int val;

        public Pair(long ne, long val, int x) {
            this.x = ne;
            this.y = val;
            this.val = x;
        }

        @Override
        public boolean equals(Object o) {
            if (this == o) return true;
            if (o == null || getClass() != o.getClass()) return false;
            Pair pair = (Pair) o;
            return x == pair.x && y == pair.y && val == pair.val;
        }

        @Override
        public int hashCode() {
            return Objects.hash(x, y, val);
        }
    }

    public static class Node {
        int x, y, val;

        public Node(int x, int y, int val) {
            this.x = x;
            this.y = y;
            this.val = val;
        }
        public Node(int x, int y) {
            this.x = x;
            this.y = y;
        }

    }


    static PrintWriter w = new PrintWriter(new OutputStreamWriter(System.out));
    static Input f = new Input(System.in);

    static class Input {
        public BufferedReader reader;
        public StringTokenizer tokenizer;

        public Input(InputStream stream) {
            reader = new BufferedReader(new InputStreamReader(stream), 32768);
            tokenizer = null;
        }

        public String next() throws IOException {

            while (tokenizer == null || !tokenizer.hasMoreTokens()) {
                tokenizer = new StringTokenizer(reader.readLine());
            }
            return tokenizer.nextToken();
        }

        public String nextLine() throws IOException {
            String str = null;
            str = reader.readLine();
            return str;
        }

        public int nextInt() throws IOException {
            return Integer.parseInt(next());
        }

        public long nextLong() throws IOException {
            return Long.parseLong(next());
        }

        public Double nextDouble() throws IOException {
            return Double.parseDouble(next());
        }
    }
}

D1. Reverse Card (Easy Version)：

题目大意：

思路解析：

a+b是b*gcd(a,b)的倍数，如果gcd(a,b) == 1 ，那么就是 a+b 是b的倍数，那么可以推出a是b的倍数，与gcd(a,b)==1违背

a+b是b*gcd(a,b)的倍数 也可以等价于a+b是b的倍数 等价于 a是b的倍数，那么 a+b应该是b*b的倍数

令 a+b == b*b a+b == 2*b*b................... a == (b-1)*b

只要a和b有这样的关系就可以称为一个有序数对，那么利用这个关系也可以求解答案了 这里在求解时可以等价n中有多少个数是 (b-1)*b的倍数

代码实现：


import java.util.*;


import java.io.*;

public class Main {

    public static void main(String[] args) throws IOException {

        int t = f.nextInt();
        while (t > 0) {
            solve();
            t--;
        }
        w.flush();
        w.close();
    }

    static int mod = 998244353;
    static long inf = (long) 1e18;


    public static void solve() throws IOException {
        int n = f.nextInt(); int m = f.nextInt();
        long ans = n;
        for (int i = 2; i <= m; i++) {
            int t = i * (i - 1);
           if (t > n) break;
           ans += (n - t) / (i * i) + 1;

        }
        w.println(ans);
    }


    public static void swap(int[] a, int i, int j) {
        int tmp = a[i];
        a[i] = a[j];
        a[j] = tmp;
    }


    public static long qkm(long a, long b, long mod) {
        long res = 1;
        while (b > 0) {
            if ((b & 1) == 1) res = res * a % mod;
            a = a * a % mod;
            b >>= 1;
        }
        return res;
    }

    public static class Pair {
        long x, y;
        int val;

        public Pair(long ne, long val, int x) {
            this.x = ne;
            this.y = val;
            this.val = x;
        }

        @Override
        public boolean equals(Object o) {
            if (this == o) return true;
            if (o == null || getClass() != o.getClass()) return false;
            Pair pair = (Pair) o;
            return x == pair.x && y == pair.y && val == pair.val;
        }

        @Override
        public int hashCode() {
            return Objects.hash(x, y, val);
        }
    }

    public static class Node {
        int x, y, val;

        public Node(int x, int y, int val) {
            this.x = x;
            this.y = y;
            this.val = val;
        }
        public Node(int x, int y) {
            this.x = x;
            this.y = y;
        }

    }


    static PrintWriter w = new PrintWriter(new OutputStreamWriter(System.out));
    static Input f = new Input(System.in);

    static class Input {
        public BufferedReader reader;
        public StringTokenizer tokenizer;

        public Input(InputStream stream) {
            reader = new BufferedReader(new InputStreamReader(stream), 32768);
            tokenizer = null;
        }

        public String next() throws IOException {

            while (tokenizer == null || !tokenizer.hasMoreTokens()) {
                tokenizer = new StringTokenizer(reader.readLine());
            }
            return tokenizer.nextToken();
        }

        public String nextLine() throws IOException {
            String str = null;
            str = reader.readLine();
            return str;
        }

        public int nextInt() throws IOException {
            return Integer.parseInt(next());
        }

        public long nextLong() throws IOException {
            return Long.parseLong(next());
        }

        public Double nextDouble() throws IOException {
            return Double.parseDouble(next());
        }
    }
}

D2. Reverse Card (Hard Version)：

题目大意：

思路解析：

将 gcd(𝑎,𝑏) 表示为 d 。假设有 a=pd𝑎=𝑝𝑑 和 b=qd𝑏=𝑞𝑑 ，那么我们知道 gcd(p,q)=1

(a+b)∣(b⋅gcd(a,b))⟺(pd+qd)∣(qd2)⟺(p+q)∣(qd)

我们知道 gcd(p+q,q)=gcd(p,q)=1，所以是 (p+q)∣d(𝑝+𝑞)∣𝑑 。

我们还知道 p≥1,q≥1 ，所以 p<d=ap≤np ，从而 p2<n 。同样，我们可以证明 q2<m 。

这里有个很关键的地方就是打表，你利用100 1233这组数据就可以找到所有合法有序对（因为这组数据遍历时间并不复杂，并且又有几百的有效有序对，那么对于我们观察答案性质是很有效的）

那我们就可以得到很多对 a 和 b，此时再观察 a/gcd(a,b) ==p, b/gcd(a,b)==q，并且统计这样序关系出现次数，发现他们的出现次数刚好可以等价于 min(n/p,m/q)/(p+q), 那么得到这个式子后就可以进行求解，打表对于构造题和数学题这类题型是非常关键的。

代码实现：


import java.util.*;


import java.io.*;

public class Main {

    public static void main(String[] args) throws IOException {

        int t = f.nextInt();
        while (t > 0) {
            solve();
            t--;
        }
        w.flush();
        w.close();
    }

    static int mod = 998244353;
    static long inf = (long) 1e18;


    public static void solve() throws IOException {
        int n = f.nextInt(); int m = f.nextInt();
        long ans = 0;
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= m; j++) {
                if (j * (i + j) > n) break;
                if (gcd(i, j) == 1){
                    ans += Math.min(m/i,n/j)/(i+j);
                }
            }
        }
        w.println(ans);
    }

    public static int gcd(int i, int j){
        if(i == 0) return j;
        if (j==0) return i;
        return gcd(j, i % j);
    }

    public static void swap(int[] a, int i, int j) {
        int tmp = a[i];
        a[i] = a[j];
        a[j] = tmp;
    }

    static long pow(long a, long b){
        long res = 1;
        while (b > 0){
            if ((b & 1) == 1) res = res * a % mod;
            a = a * a % mod;
            b >>=1;
        }
        return res;
    }
    public static long qkm(long a, long b, long mod) {
        long res = 1;
        while (b > 0) {
            if ((b & 1) == 1) res = res * a % mod;
            a = a * a % mod;
            b >>= 1;
        }
        return res;
    }

    public static class Pair {
        long x, y;
        int val;

        public Pair(long ne, long val, int x) {
            this.x = ne;
            this.y = val;
            this.val = x;
        }

        @Override
        public boolean equals(Object o) {
            if (this == o) return true;
            if (o == null || getClass() != o.getClass()) return false;
            Pair pair = (Pair) o;
            return x == pair.x && y == pair.y && val == pair.val;
        }

        @Override
        public int hashCode() {
            return Objects.hash(x, y, val);
        }
    }

    public static class Node {
        int x, y, val;

        public Node(int x, int y, int val) {
            this.x = x;
            this.y = y;
            this.val = val;
        }
        public Node(int x, int y) {
            this.x = x;
            this.y = y;
        }

    }


    static PrintWriter w = new PrintWriter(new OutputStreamWriter(System.out));
    static Input f = new Input(System.in);

    static class Input {
        public BufferedReader reader;
        public StringTokenizer tokenizer;

        public Input(InputStream stream) {
            reader = new BufferedReader(new InputStreamReader(stream), 32768);
            tokenizer = null;
        }

        public String next() throws IOException {

            while (tokenizer == null || !tokenizer.hasMoreTokens()) {
                tokenizer = new StringTokenizer(reader.readLine());
            }
            return tokenizer.nextToken();
        }

        public String nextLine() throws IOException {
            String str = null;
            str = reader.readLine();
            return str;
        }

        public int nextInt() throws IOException {
            return Integer.parseInt(next());
        }

        public long nextLong() throws IOException {
            return Long.parseLong(next());
        }

        public Double nextDouble() throws IOException {
            return Double.parseDouble(next());
        }
    }
}

E. Fenwick Tree：

题目大意：

思路解析：

给出官方题解

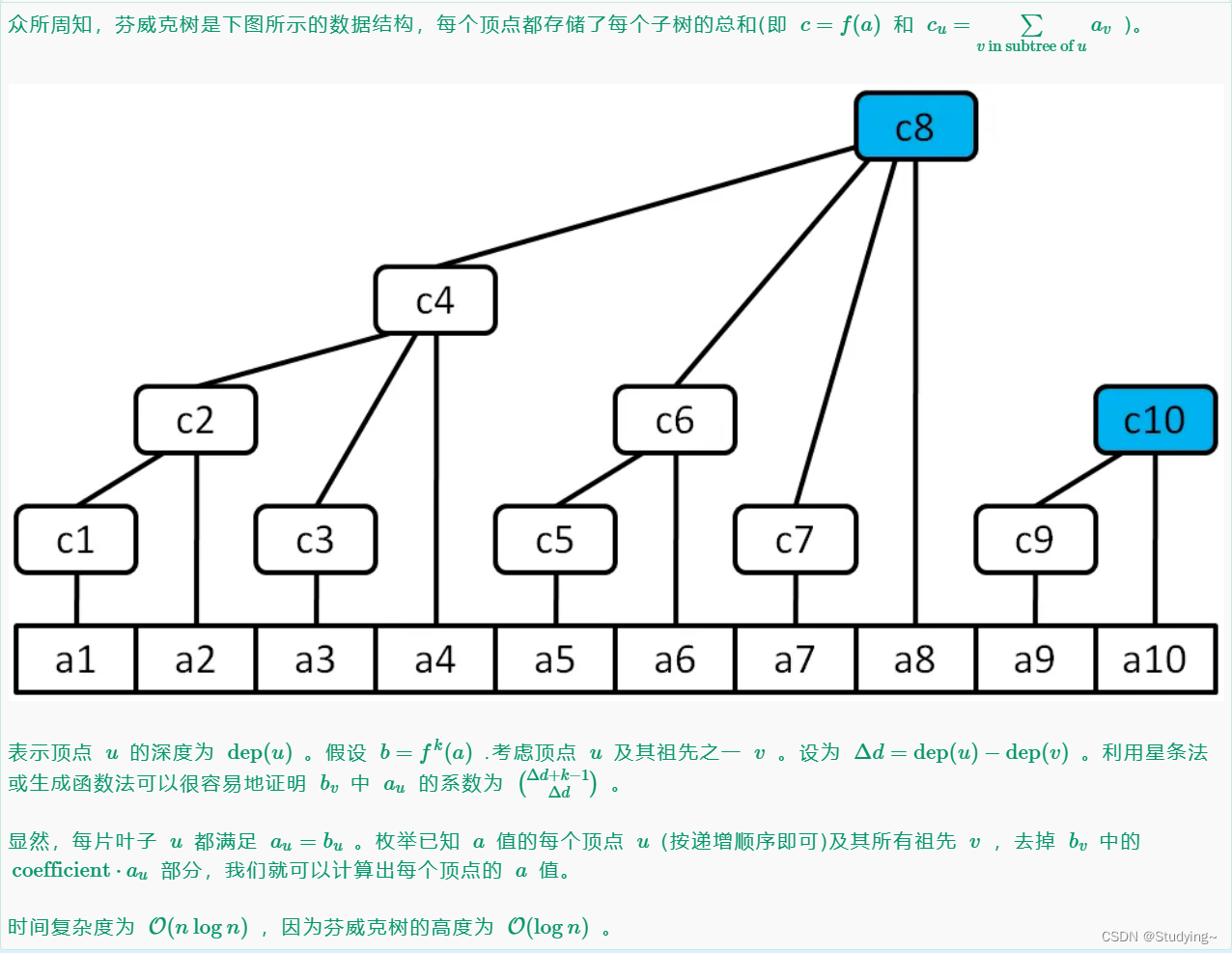
 代码实现：


import java.util.*;


import java.io.*;

public class Main {
    static int N = (int) 1e6 + 100;
    static long[] inv = new long[N];
    public static void main(String[] args) throws IOException {
        inv[0] = inv[1] = 1;
        for (int i = 2; i < N; i++) {
            inv[i] = (mod - mod /i ) * inv[mod % i] % mod;
        }
        int t = f.nextInt();
        while (t > 0) {
            solve();
            t--;
        }
        w.flush();
        w.close();
    }

    static int mod = 998244353;
    static long inf = (long) 1e18;


    public static void solve() throws IOException {
        int n = f.nextInt(); int m = f.nextInt();
        long[] a = new long[n+1];
        for (int i = 1; i <= n; i++) {
            a[i] = f.nextInt();
        }
        for (int i = 1; i <= n; i++) {
            long mul = 1;
            for (int j = i + lowbit(i), d=1; j <= n; j+=lowbit(j),++d) {
                mul = mul * (d + m - 1) % mod * inv[d] % mod;
                a[j] -= mul * a[i] % mod;
                a[j] = (a[j] + mod) % mod;
            }
        }
        for (int i = 1; i <= n; i++) {
            w.print(a[i] + " ");
        }
        w.println();
    }
    public static int lowbit(int x) {return x & -x;}

    public static int gcd(int i, int j){
        if(i == 0) return j;
        if (j==0) return i;
        return gcd(j, i % j);
    }

    public static void swap(int[] a, int i, int j) {
        int tmp = a[i];
        a[i] = a[j];
        a[j] = tmp;
    }

    static long pow(long a, long b){
        long res = 1;
        while (b > 0){
            if ((b & 1) == 1) res = res * a % mod;
            a = a * a % mod;
            b >>=1;
        }
        return res;
    }
    public static long qkm(long a, long b, long mod) {
        long res = 1;
        while (b > 0) {
            if ((b & 1) == 1) res = res * a % mod;
            a = a * a % mod;
            b >>= 1;
        }
        return res;
    }

    public static class Pair {
        long x, y;
        int val;

        public Pair(long ne, long val, int x) {
            this.x = ne;
            this.y = val;
            this.val = x;
        }

        @Override
        public boolean equals(Object o) {
            if (this == o) return true;
            if (o == null || getClass() != o.getClass()) return false;
            Pair pair = (Pair) o;
            return x == pair.x && y == pair.y && val == pair.val;
        }

        @Override
        public int hashCode() {
            return Objects.hash(x, y, val);
        }
    }

    public static class Node {
        int x, y, val;

        public Node(int x, int y, int val) {
            this.x = x;
            this.y = y;
            this.val = val;
        }
        public Node(int x, int y) {
            this.x = x;
            this.y = y;
        }

    }


    static PrintWriter w = new PrintWriter(new OutputStreamWriter(System.out));
    static Input f = new Input(System.in);

    static class Input {
        public BufferedReader reader;
        public StringTokenizer tokenizer;

        public Input(InputStream stream) {
            reader = new BufferedReader(new InputStreamReader(stream), 32768);
            tokenizer = null;
        }

        public String next() throws IOException {

            while (tokenizer == null || !tokenizer.hasMoreTokens()) {
                tokenizer = new StringTokenizer(reader.readLine());
            }
            return tokenizer.nextToken();
        }

        public String nextLine() throws IOException {
            String str = null;
            str = reader.readLine();
            return str;
        }

        public int nextInt() throws IOException {
            return Integer.parseInt(next());
        }

        public long nextLong() throws IOException {
            return Long.parseLong(next());
        }

        public Double nextDouble() throws IOException {
            return Double.parseDouble(next());
        }
    }
}

F. Long Way to be Non-decreasing：

题目大意：

思路解析：

代码实现：

#include <bits/stdc++.h>
 
namespace FastIO {
	template <typename T> inline T read() { T x = 0, w = 0; char ch = getchar(); while (ch < '0' || ch > '9') w |= (ch == '-'), ch = getchar(); while ('0' <= ch && ch <= '9') x = x * 10 + (ch ^ '0'), ch = getchar(); return w ? -x : x; }
	template <typename T> inline void write(T x) { if (!x) return; write<T>(x / 10), putchar(x % 10 ^ '0'); }
	template <typename T> inline void print(T x) { if (x < 0) putchar('-'), x = -x; else if (x == 0) putchar('0'); write<T>(x); }
	template <typename T> inline void print(T x, char en) { if (x < 0) putchar('-'), x = -x; else if (x == 0) putchar('0'); write<T>(x), putchar(en); }
}; using namespace FastIO;
 
#define MAXM 1000001
int dep[MAXM], id[MAXM], dfn[MAXM], to[MAXM], sz[MAXM], tot = 0;
std::vector<int> ch[MAXM];
void dfs(int u) {
	sz[u] = 1, dfn[u] = ++tot;
	for (int v : ch[u]) {
		dep[v] = dep[u] + 1, id[v] = id[u];
		dfs(v), sz[u] += sz[v];
	}
}
inline bool inSub(int u, int v) /* v \in u ? */ { return dfn[u] <= dfn[v] && dfn[v] < dfn[u] + sz[u]; }
constexpr int INF = 0x3f3f3f3f;
inline int query(int u, int v) /* u -> v */ {
	if (u == v) return 0;
	if (id[u] != id[v]) return INF;
	int res = INF;
	if (inSub(v, u)) res = dep[u] - dep[v];
	if (inSub(v, to[id[u]])) res = std::min(dep[u] - dep[v] + dep[to[id[u]]] + 1, res);
	// printf("query(%d, %d) = %d\n", u, v, res);
	return res;
}
 
#define MAXN 1000001
int a[MAXN], N, M;
bool check(int val) {
	// printf("check %d\n", val);
	int lst = 1;
	for (int i = 1; i <= N; ++i) {
		while (lst <= M && query(a[i], lst) > val) ++lst;
		if (lst > M) return false;
		// printf("a[%d] = %d\n", i, lst);	
	}
	return true;
}
 
namespace DSU {
	int fa[MAXM];
	void inis(int n) { for (int i = 1; i <= n; ++i) fa[i] = i; }
	inline int find(int x) { return x == fa[x] ? x : fa[x] = find(fa[x]); }
	inline bool merge(int x, int y) { if (find(x) == find(y)) return false; fa[fa[x]] = fa[y]; return true; }
}; using namespace DSU;
 
int main() {
	int T = read<int>();
	while (T--) {
		N = read<int>(), M = read<int>(), inis(M);
		for (int i = 1; i <= N; ++i) a[i] = read<int>();
		for (int x = 1; x <= M; ++x) dep[x] = id[x] = dfn[x] = to[x] = sz[x] = 0, ch[x].clear();
		tot = 0;
		for (int i = 1, p; i <= M; ++i) {
			p = read<int>();
			if (merge(i, p)) ch[p].push_back(i); else to[i] = p;
		}
		for (int i = 1; i <= M; ++i) if (to[i] > 0) id[i] = i, dfs(i);
		if (!check(M)) { puts("-1"); continue; }
		int L = 0, R = M;
		while (L < R) {
			int mid = L + R >> 1;
			if (check(mid)) R = mid; else L = mid + 1;
		}
		print<int>(R, '\n');
	}
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1637577.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【无线通信开发应用】nRF905数据手册深度解读

【无线通信开发应用】nRF905数据手册深度解读

希望通过两个stm32、两个nRF905无线通信模块、串口来实现两机通信。具体功能为&#xff1a; 板子A、B分别包含一个stm32单片机和一个nRF905无线模块&#xff0c;欲实现板子A、B之间的通信。 其中&#xff0c;PC端串口助手可向板子A的stm32发送字符‘A’控制板子B上的LED亮灯&am…
阅读更多...
算法系列--多源BFS问题

算法系列--多源BFS问题

&#x1f495;"对相爱的人来说&#xff0c;对方的心意&#xff0c;才是最好的房子。"&#x1f495; 作者&#xff1a;Lvzi 文章主要内容&#xff1a;算法系列–多源BFS问题 大家好,今天为大家带来的是算法系列--多源BFS问题 前言: 之前我们已经学习过单源的最短路问…
阅读更多...
质谱原理与仪器3-笔记

质谱原理与仪器3-笔记

质谱原理与仪器3-笔记 一、质量分析器类型1、聚焦磁场分析器&#xff1a;A、单聚焦磁场分析器B、双聚焦磁场分析器 2、四极杆质量分析器3、飞行时间质谱仪(Time of Flight MS, TOF-MS)4、离子阱质量分析器 二、质谱仪的主要性能指标1、质量范围(mass range)2、分辨率(resolutio…
阅读更多...
面试经典150题——Z 字形变换

面试经典150题——Z 字形变换

面试经典150题 day22 题目来源我的题解方法一 使用StringBuilder数组模拟矩阵方法二 找规律直接构造 题目来源 力扣每日一题&#xff1b;题序&#xff1a;6 我的题解 方法一 使用StringBuilder数组模拟矩阵 如果numRows是1&#xff0c;则直接返回s。 否则&#xff0c;创建nu…
阅读更多...
python实现的基于单向循环链表插入排序

python实现的基于单向循环链表插入排序

相比于定义一个循环双向链表来实现插入排序来说&#xff0c;下面的实现采用一个单向循环链表来实现&#xff0c;并且不需要定义一个单向循环链表类&#xff0c;而是把一个list&#xff08;数组/顺序表&#xff09;当成单向循环链表来用&#xff0c;list的元素是一个包含两个元素…
阅读更多...
26.统一网关Gateway

26.统一网关Gateway

网关的功能 1.身份认证&#xff0c;权限的校验。 2.服务的路由&#xff0c;负载均衡。用户请求被分配到哪一个微服务。一个微服务可以有多个实例&#xff0c;所以使用负载均衡。 3.请求限流。 springcloud网关实现有两种&#xff1a;gateway, zuul zuul是基于servlet实现的…
阅读更多...
Enhancing Diffusion——利用三维透视几何约束增强扩散模型

Enhancing Diffusion——利用三维透视几何约束增强扩散模型

概述 透视在艺术中被广泛研究&#xff0c;但现代高质量图像生成方法却缺乏透视精度。新的生成模型引入了几何约束&#xff0c;通过训练过程提高透视精度。这样可以生成更逼真的图像&#xff0c;并提高相关深度估计模型的性能。 最近的图像生成技术使研究人员能够创造性地进行…
阅读更多...
TCP/IP和HTTP协议

TCP/IP和HTTP协议

TCP/IP OSI 七层模型在提出时的出发点是基于标准化的考虑&#xff0c;而没有考虑到具体的市场需求&#xff0c;使得该模型结构复杂&#xff0c;部分功能冗余&#xff0c;因而完全实现 OSI 参考模型的系统不多。而 TCP/IP 参考模型直接面向市场需求&#xff0c;实现起来也比较…
阅读更多...
App一键直达，Xinstall助力提升用户体验

App一键直达，Xinstall助力提升用户体验

在这个移动互联网时代&#xff0c;App已经成为了我们日常生活中不可或缺的一部分。然而&#xff0c;每当我们在浏览器或社交平台上看到一个有趣的App推荐&#xff0c;点击下载后却往往要经历一系列繁琐的跳转和确认过程&#xff0c;这无疑大大降低了用户体验。那么&#xff0c;…
阅读更多...
工业三废数据集（工业烟粉尘排放量、工业二氧化硫排放量、工业废水排放量）2006-2021年

工业三废数据集（工业烟粉尘排放量、工业二氧化硫排放量、工业废水排放量）2006-2021年

01、数据介绍 工业三废是指工业生产过程中排出的废气、废水和废渣 工业二氧化硫排放量指企业在燃料燃烧和生产工艺过程中排入大气的二氧化硫数量。 工业烟粉尘排放量是指企业在生产工艺过程中排放的烟尘和粉尘等颗粒物重量。 工业废水排放量是指企业在生产过程中产生的废水…
阅读更多...
GPG的使用

GPG的使用

这里写自定义目录标题 安装加密程序生成加密密钥怎么备份自己的密钥就可以使用公钥加密邮件信息了 安装加密程序 下载gpg4win&#xff1a; https://www.gpg4win.org/index.html 免费的&#xff0c;如果使用的是苹果电脑&#xff0c;使用https://gpgtools.org/。 如果是linux&a…
阅读更多...
Go Web 开发基础【用户登录、注册、验证】

Go Web 开发基础【用户登录、注册、验证】

前言 这篇文章主要是学习怎么用 Go 语言&#xff08;Gin&#xff09;开发Web程序&#xff0c;前端太弱了&#xff0c;得好好补补课&#xff0c;完了再来更新。 1、环境准备 新建项目&#xff0c;生成 go.mod 文件&#xff1a; 出现报错&#xff1a;go: modules disabled by G…
阅读更多...
【webrtc】RemoteAudioSource的创建线程

【webrtc】RemoteAudioSource的创建线程

m98 代码&#xff1a;I:\webrtc m98_yjf\src\pc\rtp_transmission_manager.cc RtpTransmissionManager::CreateReceiver 在信令线程创建receiver receiver 是&#xff1a; rtc::scoped_refptr<RtpReceiverProxyWithInternal<RtpReceiverInternal>>receiver;其实际…
阅读更多...
uniapp微信小程序开发踩坑日记：由于图表数据渲染不出来，我第一次在项目中用watch函数监听数据变化

uniapp微信小程序开发踩坑日记：由于图表数据渲染不出来，我第一次在项目中用watch函数监听数据变化

一、发现问题 在我们团队自己开发的微信小程序中&#xff0c;引入了Echarts图表库 然后突然有一天&#xff0c;后端队友反应图表渲染有问题。后面我去试了一下&#xff0c;确实20次里面必有一次数据渲染不出来 断定代码没问题&#xff0c;于是我们将其鉴定为玄学 二、问题原因…
阅读更多...
笔记本无线网络共享给有线使用

笔记本无线网络共享给有线使用

1.鼠标右击wifi图标选择打开网络和Internet设置 2.选择WLAN项&#xff0c;点击进入更改适配器选项 3.进入到以下界面&#xff0c;右击以太网选择启动&#xff08;不确定的话可以在设备管理器查看网卡&#xff09; 4.右击WLAN选项&#xff0c;点击属性 5.点击共享&#xff0…
阅读更多...
日期类的实现，const成员

日期类的实现，const成员

目录 一&#xff1a;日期类实现 二&#xff1a;const成员 三&#xff1a;取地址及const取地址操作符重载 一&#xff1a;日期类实现 //头文件#include <iostream> using namespace std;class Date {friend ostream& operator<<(ostream& out, const Dat…
阅读更多...
AI大模型探索之路-训练篇9：大语言模型Transformer库-Pipeline组件实践

AI大模型探索之路-训练篇9：大语言模型Transformer库-Pipeline组件实践

系列篇章&#x1f4a5; AI大模型探索之路-训练篇1&#xff1a;大语言模型微调基础认知 AI大模型探索之路-训练篇2&#xff1a;大语言模型预训练基础认知 AI大模型探索之路-训练篇3&#xff1a;大语言模型全景解读 AI大模型探索之路-训练篇4&#xff1a;大语言模型训练数据集概…
阅读更多...
大连宇都环境 | 成都5月水科技大会暨技术装备成果展览会

大连宇都环境 | 成都5月水科技大会暨技术装备成果展览会

中华环保联合会水环境治理专业委员会 秘书处 王小雅 13718793867 —— 展位号&#xff1a;A09 —— 一、企业介绍 大连宇都环境成立于2002年&#xff0c;公司20年 MBBR填料产品及工艺技术&#xff0c;&#xff0c;构建了研发、制造、设计、工程、运营链式服务能力&#xff…
阅读更多...
CGAL 点云数据生成DSM、DTM、等高线和数据分类

CGAL 点云数据生成DSM、DTM、等高线和数据分类

原文链接 CGAL 点云数据生成DSM、DTM、等高线和数据分类 - 知乎 在GIS应用软件中使用的许多传感器(如激光雷达)都会产生密集的点云。这类应用软件通常利用更高级的数据结构&#xff1a;如&#xff1a;不规则三角格网 (TIN)是生成数字高程模型 (DEM) 的基础&#xff0c;也可以利…
阅读更多...
docker系列8：容器卷挂载(上)

docker系列8：容器卷挂载(上)

传送门 docker系列1&#xff1a;docker安装 docker系列2&#xff1a;阿里云镜像加速器 docker系列3&#xff1a;docker镜像基本命令 docker系列4&#xff1a;docker容器基本命令 docker系列5&#xff1a;docker安装nginx docker系列6&#xff1a;docker安装redis docker系…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023