深入理解多层感知机MLP

1. 基础理论

神经网络基础：

目标：了解神经网络的结构，包括神经元、权重、偏置和激活函数。

神经网络是由多个层次的神经元组成的网络，它模拟了人脑处理信息的方式。每个神经元可以接收输入、处理输入并生成输出。这一过程涉及到权重、偏置和激活函数的使用。让我们详细探讨这些组成部分及其在神经网络中的角色。

神经元（Neuron）

神经元是神经网络的基本单元。在生物学中，神经元接收来自其他神经细胞的信号，处理这些信号，然后传输到其他神经元。在人工神经网络中，每个“人工神经元”或节点类似地接收输入，对输入进行加权求和，加上一个偏置项，然后通过一个激活函数生成输出。

示例：
想象你正在构建一个用于预测房价的神经网络。每个神经元可能接收如房屋的面积、位置、年龄等信息作为输入。这些输入通过与权重的乘积被加总，这个加权和代表了房屋的特征对其价格的总影响。

权重（Weights）

权重控制了神经网络中一个神经元输入的重要性。在训练过程中，网络通过调整权重来学习哪些特征更重要，从而提高预测的准确性。

示例：
在房价预测模型中，如果发现房屋的位置对价格影响最大，相应连接到位置输入的权重将会调整得更大，使得模型更多地考虑位置的影响。

偏置（Bias）

https://stackoverflow.com/questions/2480650/what-is-the-role-of-the-bias-in-neural-networks

偏置是一个额外的输入到神经元中，总是为1，它的权重（偏置项）允许神经元偏移其输出，以更好地拟合数据。

示例：
即使所有其他输入都是0，偏置也允许模型输出非零值。例如，在房价模型中，偏置可以帮助模型输出最低的基准价格，即使没有其他信息。

激活函数（Activation Function）

激活函数决定了神经元的输出，它可以引入非线性因素，使得神经网络能够学习和执行更复杂的任务。

常见的激活函数包括：

很好，深入了解激活函数是理解神经网络如何工作的关键部分。让我们分别详细探讨 Sigmoid 和 ReLU 这两个激活函数，并通过具体的例子来说明它们的应用和影响。

Sigmoid 激活函数

定义

Sigmoid 函数是一个典型的 S 形曲线，数学表达式为：
$\sigma(x) = \frac{1}{1 + e^{-x}}$
这个函数将任意值的输入映射到 (0, 1) 之间，非常适合需要输出概率预测的任务，如二分类问题。

应用示例

二分类问题：假设我们正在开发一个逻辑回归模型来预测邮件是否为垃圾邮件。在这种情况下，模型的输出可以是一个实数值，这个值经过 Sigmoid 函数处理后转换为概率值。

模型结构：输入特征可能包括邮件中的关键词频率、发件人信誉等，这些输入经过权重加总后，再加上偏置项，最后的结果通过 Sigmoid 函数转换为一个介于0和1之间的值。
输出解释：如果 Sigmoid 输出值大于 0.5，模型预测邮件为垃圾邮件；如果小于或等于 0.5，预测邮件不是垃圾邮件。

优点和缺点

优点：直观，输出易于解释为概率。
缺点：梯度消失问题（在 x 的值非常大或非常小的情况下，Sigmoid 的导数接近于 0，这会导致在梯度下降过程中更新非常缓慢或停滞不前）。

ReLU 激活函数

定义

ReLU（Rectified Linear Unit）函数是一个分段线性函数，数学表达式为：
$\max(0, x)$
这意味着如果输入 x 是正数，则输出 x；如果是负数，则输出 0。这种简单的非线性形式使得 ReLU 在隐藏层中非常受欢迎。

应用示例

图像识别任务：假设我们正在训练一个卷积神经网络来识别图像中的对象。ReLU 函数通常用于网络的隐藏层。

模型结构：在多层网络中，每个卷积层后通常会跟一个 ReLU 层，这有助于引入非线性，使网络能够学习更复杂的特征。
功能：ReLU 有助于加快神经网络的训练，因为它在正区间的梯度总是 1，这避免了梯度消失问题，并且计算上比 Sigmoid 和 Tanh 等函数简单得多。

优点和缺点

优点：计算简单，加速神经网络的收敛，解决了部分梯度消失问题。
缺点：死亡 ReLU 问题（一些神经元可能永远不会被激活，导致相应的权重无法更新）。

通过这两个例子，我们可以看到不同激活函数的选择对模型的性能和训练动态有重要影响。Sigmoid 适合输出层，尤其是需要概率输出的场景，而 ReLU 则适合用在多层网络的隐藏层，特别是在需要处理非线性复杂数据，如图像和声音的场合。

Tanh（Hyperbolic Tangent）激活函数

输出值在-1到1之间，形状和Sigmoid类似，但数据标准化后的表现通常更好。

前向传播和反向传播

理解数据如何在网络中前向传播以及如何通过反向传播算法调整权重。

前向传播和反向传播是神经网络训练过程中的两个核心步骤。这些过程对于理解神经网络是如何学习和更新其权重的至关重要。

前向传播（Forward Propagation）

定义与过程
前向传播是神经网络计算和输出预测的过程。它从输入层开始，通过隐藏层（如果有的话），最终到达输出层。在每一层，每个神经元接收来自前一层的输入，这些输入根据前一层的输出和相应的权重进行加权求和，加上一个偏置项，然后通过激活函数处理以产生这一层的输出。

示例：简单的前向传播
想象一个简单的神经网络，它有一个输入层、一个隐藏层和一个输出层：

输入层：假设我们的任务是基于房屋的面积和年龄预测房价。输入层接收两个输入：面积（1200平方英尺）和年龄（10年）。
隐藏层：有两个神经元。每个神经元都有权重和偏置，使用ReLU作为激活函数。假设权重为面积（w1 = 0.5），年龄（w2 = -0.3），偏置为b = 2。
输出层：最终预测房价，使用一个神经元，激活函数为线性函数（即输出值是输入值的直接映射）。

前向传播计算：

隐藏层第一个神经元的输入值为 0.5*1200 + -0.3*10 + 2 = 596，ReLU激活后输出为 max(0, 596) = 596。
假设输出层的权重是 0.4，没有激活函数，输出层的输出即为 0.4 * 596 = 238.4。这是模型对房价的预测。

反向传播（Backpropagation）

https://home.agh.edu.pl/~vlsi/AI/backp_t_en/backprop.html

定义与过程
反向传播是一个用于训练神经网络的方法，通过它网络可以学习从数据中预测错误中改进。在前向传播完成后，网络会计算输出和真实值之间的误差（通常使用损失函数如均方误差）。反向传播的目标是将这个误差反馈到网络的每一层，逐步调整每个权重和偏置，以减少未来预测的误差。

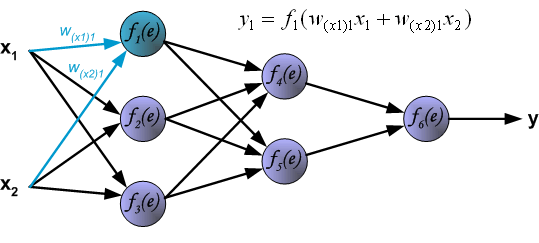
为了说明这一过程，使用了具有两个输入和一个输出的三层神经网络，如下图所示：

Each neuron is composed of two units. First unit adds products of weights coefficients and input signals. The second unit realise nonlinear function, called neuron activation function. Signal e is adder output signal, and y = f(e) is output signal of nonlinear element. Signal y is also output signal of neuron.
每个神经元由两个单元组成。第一个单元将权重系数和输入信号的乘积相加。第二个单元实现非线性函数，称为神经元激活函数。信号e为加法器输出信号，y=f(e)为非线性元件的输出信号。信号y也是神经元的输出信号。

To teach the neural network we need training data set. The training data set consists of input signals (x1 and x2 ) assigned with corresponding target (desired output) z. The network training is an iterative process. In each iteration weights coefficients of nodes are modified using new data from training data set. Modification is calculated using algorithm described below: Each teaching step starts with forcing both input signals from training set. After this stage we can determine output signals values for each neuron in each network layer. Pictures below illustrate how signal is propagating through the network, Symbols w(xm)n represent weights of connections between network input xm and neuron n in input layer. Symbols yn represents output signal of neuron n.
为了教授神经网络，我们需要训练数据集。训练数据集由分配有相应目标（所需输出）z 的输入信号（x 1 和 x 2 ）组成。网络训练是一个迭代过程。在每次迭代中，使用训练数据集中的新数据修改节点的权重系数。使用下述算法计算修改：每个教学步骤都从强制来自训练集的两个输入信号开始。在此阶段之后，我们可以确定每个网络层中每个神经元的输出信号值。下图说明了信号如何在网络中传播，符号 w (xm)n 表示网络输入 x m 与输入层神经元 n 之间的连接权重。符号y n 表示神经元n的输出信号。

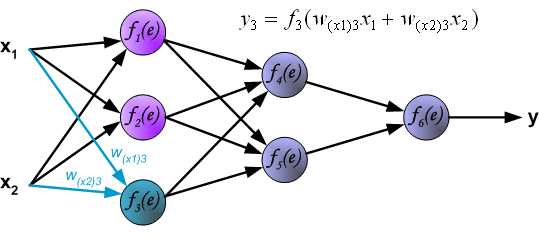
Propagation of signals through the hidden layer. Symbols wmn represent weights of connections between output of neuron m and input of neuron n in the next layer.
通过隐藏层传播信号。符号w mn 表示下一层神经元m的输出与神经元n的输入之间的连接权重。

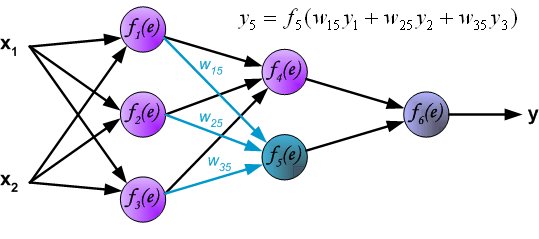
Propagation of signals through the output layer.
通过输出层传播信号。

It is impossible to compute error signal for internal neurons directly, because output values of these neurons are unknown. For many years the effective method for training multiplayer networks has been unknown. Only in the middle eighties the backpropagation algorithm has been worked out. The idea is to propagate error signal d (computed in single teaching step) back to all neurons, which output signals were input for discussed neuron.
直接计算内部神经元的误差信号是不可能的，因为这些神经元的输出值是未知的。多年来，训练多人网络的有效方法一直未知。直到八十年代中期，反向传播算法才被研究出来。这个想法是将误差信号 d（在单个教学步骤中计算）传播回所有神经元，其输出信号是所讨论神经元的输入。

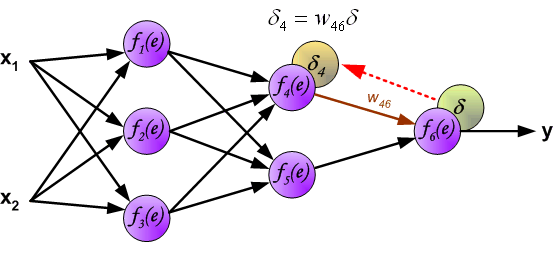
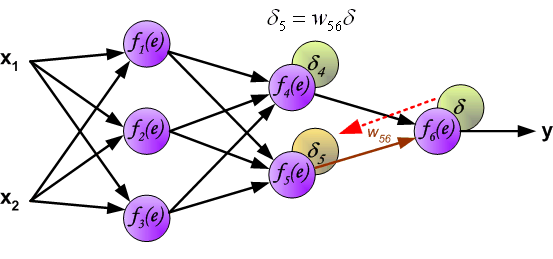
The weights’ coefficients wmn used to propagate errors back are equal to this used during computing output value. Only the direction of data flow is changed (signals are propagated from output to inputs one after the other). This technique is used for all network layers. If propagated errors came from few neurons they are added. The illustration is below:
用于传播误差的权重系数 w mn 等于计算输出值期间使用的权重系数。仅改变数据流的方向（信号从输出依次传播到输入）。该技术用于所有网络层。如果传播的错误来自少数神经元，则会添加它们。图示如下：

When the error signal for each neuron is computed, the weights coefficients of each neuron input node may be modified. In formulas below df(e)/de represents derivative of neuron activation function (which weights are modified).
当计算每个神经元的误差信号时，可以修改每个神经元输入节点的权重系数。在下面的公式中，df(e)/de 表示神经元激活函数的导数（其权重被修改）。

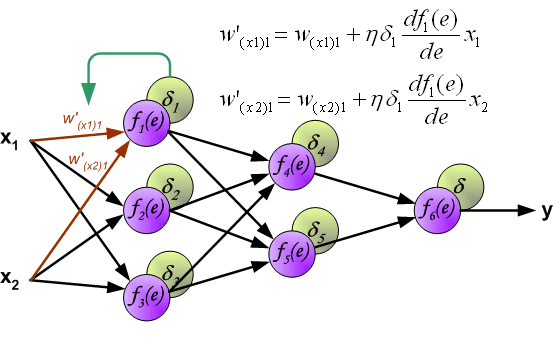
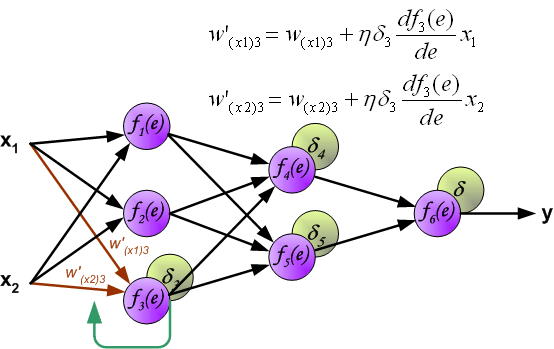
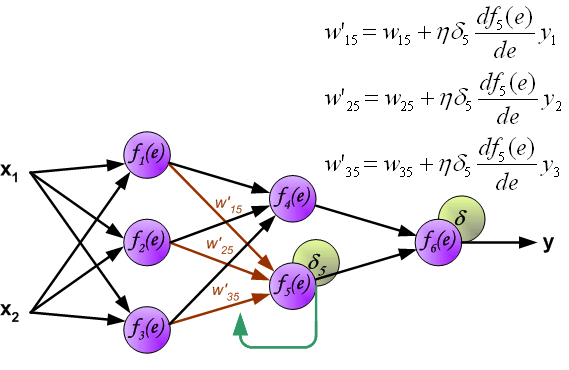
Coefficient h affects network teaching speed. There are a few techniques to select this parameter. The first method is to start teaching process with large value of the parameter. While weights coefficients are being established the parameter is being decreased gradually. The second, more complicated, method starts teaching with small parameter value. During the teaching process the parameter is being increased when the teaching is advanced and then decreased again in the final stage. Starting teaching process with low parameter value enables to determine weights coefficients signs.
系数h影响网络教学速度。有几种方法可以选择此参数。第一种方法是用较大的参数值开始示教过程。在建立权重系数的同时，参数逐渐减小。第二种更复杂的方法以较小的参数值开始示教。在示教过程中，随着示教的进行，该参数逐渐增大，在示教的最后阶段，该参数又再次减小。以低参数值开始教学过程可以确定权重系数符号。

示例：简单的反向传播
继续上面的房价预测例子，假设真实房价是 250,000 美元，而我们的预测是 238,400 美元。

损失计算：使用均方误差，误差为 (250000 - 238400)^2 = 134560000。
误差反向传播：
- 输出层误差对权重的梯度计算为：误差对输出层输出的导数乘以输出层输入（即隐藏层的输出）。
- 这个梯度用于调整输出层的权重。
- 然后，计算隐藏层的误差梯度，调整隐藏层的权重和偏置。

具体操作（需要后面细细理解）：

输出层权重的梯度：导数为 2*(250000 - 238400)*1 = 23200（假设学习率为0.01），权重更新为 0.4 + 0.01 * 23200 = 2.32。
类似地更新隐藏层权重和偏置。

通过反复执行前向传播和

反向传播，并调整权重和偏置，神经网络在训练过程中逐渐学习并减少预测误差，最终得到更精确的模型。

损失函数

学习不同类型的损失函数，包括均方误差、交叉熵等，并了解它们在不同问题中的应用。

在神经网络和机器学习中，损失函数是用于评估模型预测与实际数据之间差异的函数。它是优化过程的核心，用于调整模型参数（如权重和偏置），以最小化预测误差。不同的任务和数据类型可能需要不同的损失函数。以下是一些最常用的损失函数及其具体应用的例子：

均方误差（Mean Squared Error, MSE）

定义：
$\frac{1}{N} \sum_{i=1}^N (y_i - \hat{y}_i)^2$
其中，$(y_i) $KaTeX parse error: Can't use function '$' in math mode at position 4: 是第 \̲(̲i$ 个实际值，$ (\hat{y}_i)$ 是预测值，$(N) $\是样本数量。

应用场景：
均方误差是回归问题中最常用的损失函数。它测量预测值和实际值之间差异的平方和的平均值，是衡量预测准确性的重要指标。

示例：
假设你正在开发一个模型来预测房屋价格，基于特征如房屋大小、位置和建造年份。使用MSE作为损失函数可以帮助你衡量模型预测价格与市场实际价格之间的平均误差大小，从而不断调整模型以提高预测的准确性。

交叉熵损失（Cross-Entropy Loss）

定义：
对于二分类问题：
$KaTeX parse error: Undefined control sequence: \[ at position 2: \̲[̲ CE = -\sum_{i=…$
对于多分类问题：
$KaTeX parse error: Undefined control sequence: \[ at position 2: \̲[̲ CE = -\sum_{i=…$
其中，$(y_{i,c}) $是一个独热编码的标签向量，表示实际类别，是$ (\hat{y}_{i,c}) $模型预测的概率分布。

应用场景：
交叉熵损失广泛应用于分类问题，尤其是当输出可以被解释为概率时。它测量实际输出分布和预测分布之间的差异。

示例：
在开发一个用于图像识别的卷积神经网络时，比如识别图片中的猫和狗，交叉熵损失可以帮助优化模型，确保预测概率尽可能接近实际标签。如果模型对一张猫的图片预测为狗的概率过高，交叉熵损失会增加，激励模型调整其内部参数，减少这种误分类。

对数损失（Log Loss）

定义：
对数损失可以视为二分类交叉熵损失的一个特例，其定义与上述二分类交叉熵相同。

应用场景：
对数损失适用于二分类问题中，当预测结果表示为概率时。

示例：
在金融行业，预测交易是否为欺诈性交易是常见的问题。使用对数损失可以直接优化模型的预测概率，使模型能更准确地预测交易的真实类别。

结论

选择合适的损失函数对于训练有效的机器学习模型至关重要。损失函数的选择应基于具体的应用需求，如回归问题通常选择MSE，分类问题则更倾向于使用交叉熵。了解每种损失函数的数学定义和适用场景可以帮

助开发者更好地设计和优化模型。

2. 核心网络架构

多层感知机（MLP）

https://cleverbobo.github.io/2020/08/30/bp/

节点结构

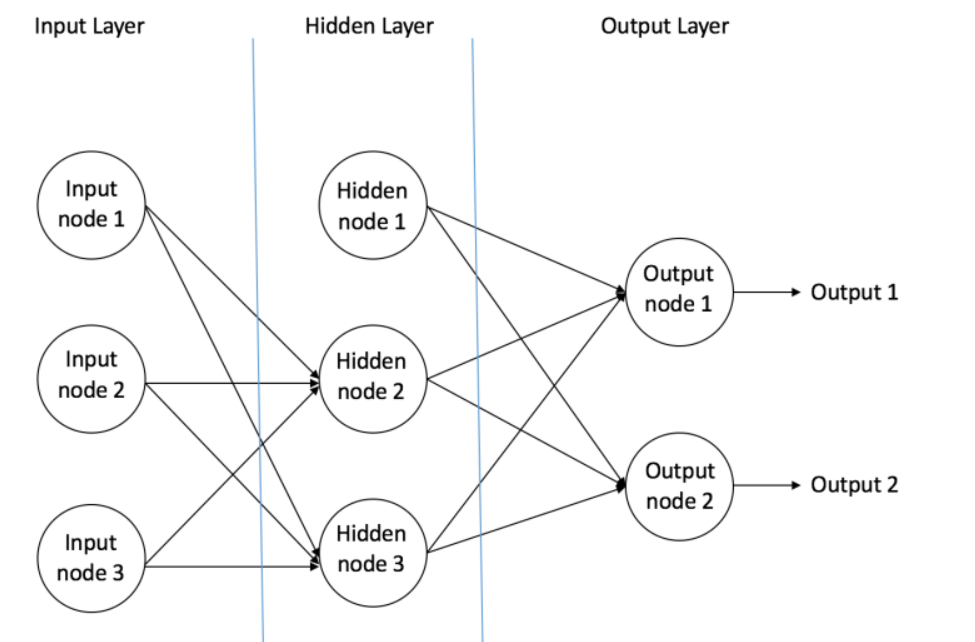
MLP的结构如图所示，主要由三部分组成，至少要有一个隐藏层。

输入节点（Input Nodes）：输入节点从外部世界提供信息，总称为「输入层」。在输入节点中，不进行任何的计算，仅向隐藏节点传递信息。
隐藏节点（Hidden Nodes）：隐藏节点和外部世界没有直接联系（由此得名）。这些节点进行计算，并将信息从输入节点传递到输出节点。隐藏节点总称为「隐藏层」。尽管一个前馈神经网络只有一个输入层和一个输出层，但网络里可以没有隐藏层（如果没有隐藏层，激活函数选择sigmod，那么就变成逻辑回归了），也可以有多个隐藏层。
输出节点（Output Nodes）：输出节点总称为「输出层」，负责计算，并从网络向外部世界传递信息。

数据前馈

以之前的结构为例：

(1) 输入层：输入层有三个节点。偏置节点值为 1。其他两个节点，X1 和 X2 取自外部输入（皆为根据输入数据集取的数字值）。和上文讨论的一样，在输入层不进行任何计算，所以输入层节点的输出是 1、X1 和 X2 三个值被传入隐藏层。

(2) 隐藏层：隐藏层也有三个节点，偏置节点输出为 1。隐藏层其他两个节点的输出取决于输入层的输出（1，X1，X2）以及连接上所附的权重。图中显示了隐藏层（高亮）中一个输出的计算方式。其他隐藏节点的输出计算同理。需留意 f 指代激活函数。这些输出会作为输出层的输入。

(3) 输出层：输出层有两个节点，从隐藏层接收输入，并执行类似高亮出的隐藏层的计算。这些作为计算结果的计算值（Y1 和 Y2）就是多层感知器的输出。

给出一系列特征 X = (x1, x2, …) 和目标 Y，一个多层感知器可以以分类或者回归为目的，学习到特征和目标之间的关系,从而建立模型。为了更好的理解多层感知器，我们举一个例子。假设我们有这样一个学生分数数据集：

两个输入栏表示了学生学习的时间和期中考试的分数。最终结果栏可以有两种值，1 或者 0，来表示学生是否通过的期末考试。例如，我们可以看到，如果学生学习了 35 个小时并在期中获得了 67 分，他 / 她就会通过期末考试。现在我们假设我们想预测一个学习了 25 个小时并在期中考试中获得 70 分的学生是否能够通过期末考试。

这是一个二元分类问题，那么多层感知机又是如何利用这么多的数据的到我们想要的结果呢？
首先，对网络中所有的权重进行随机分配，假设从输入连接到这些节点的权重分别为 w1、w2 和 w3（如图所示）。神经网络会将第一个训练样本作为输入，那么网络的输入=[35, 67]，涉及到的节点的输出 V 可以按如下方式计算（f 是类似 Sigmoid 的激活函数）：V = f(1×w1 + 35×w2 + 67×w3），最后的得到我们的输出结果，假设输出层两个节点的输出概率分别为 0.4 和 0.6（因为权重随机，输出也会随机），但是我们期望的网络输出（目标）=[1, 0]，可以看出两者之间的差距还是蛮大的，那么我们该如何调整权重，使得输出的结果更加接近目标呢？这一点，我将在下一部分讲解，也就是我们的优化算法。

误差后馈

下面我们将介绍一个多层感知器如何调整权重：

反向传播误差，通常缩写为「BackProp」，是几种训练人工神经网络的方法之一。这是一种监督学习方法，即通过标记的训练数据来学习（有监督者来引导学习）。简单说来，BackProp 就像「从错误中学习」。监督者在人工神经网络犯错误时进行纠正。一个人工神经网络包含多层的节点: 输入层，隐藏层和输出层。相邻层节点的连接都有配有「权重」。学习的目的是为这些边缘分配正确的权重。通过输入向量，这些权重可以决定输出向量。在监督学习中，训练集是已标注的。这意味着对于一些给定的输入，我们知道期望的输出（标注）。
反向传播算法：**最初，所有的边权重（edge weight）都是随机分配的。**对于所有训练数据集中的输入，人工神经网络都被激活，并且观察其输出。这些输出会和我们已知的、期望的输出进行比较，误差会「传播」回上一层。该误差会被标注，权重也会被相应的「调整」。该流程重复，直到输出误差低于制定的标准。上述算法结束后，我们就得到了一个学习过的人工神经网络，该网络被认为是可以接受「新」输入的。该人工神经网络可以说从几个样本（标注数据）和其错误（误差传播）中得到了学习。

现在我们知道了反向传播的原理，我们回到上面的学生分数数据集。

如图所示的多层感知器，其输入层有两个节点（除了偏置节点以外），两个节点分别接收「学习小时数」和「期中考试分数」。感知器也有一个包含两个节点的隐藏层（除了偏置节点以外）。输出层也有两个节点——上面一个节点输出「通过」的概率，下面一个节点输出「不通过」的概率。
在分类任务中，我们通常在感知器的输出层中使用 Softmax 函数作为激活函数，以保证输出的是概率并且相加等于 1。Softmax 函数接收一个随机实值的分数向量，转化成多个介于 0 和 1 之间、并且总和为 1 的多个向量值。所以，在这个例子中：概率（Pass）+概率（Fail）=1
在上一小节，我主要介绍了数据的前向传播，那么下面来重点讲解误差反向传播和权重更新：计算输出节点的总误差，并将这些误差用反向传播算法传播回网络，以计算梯度。接下来，我们使用类似梯度下降之类的算法来调整网络中的所有权重，目的是减少输出层的误差。下图展示了这一过程（暂时忽略图中的数学等式）。

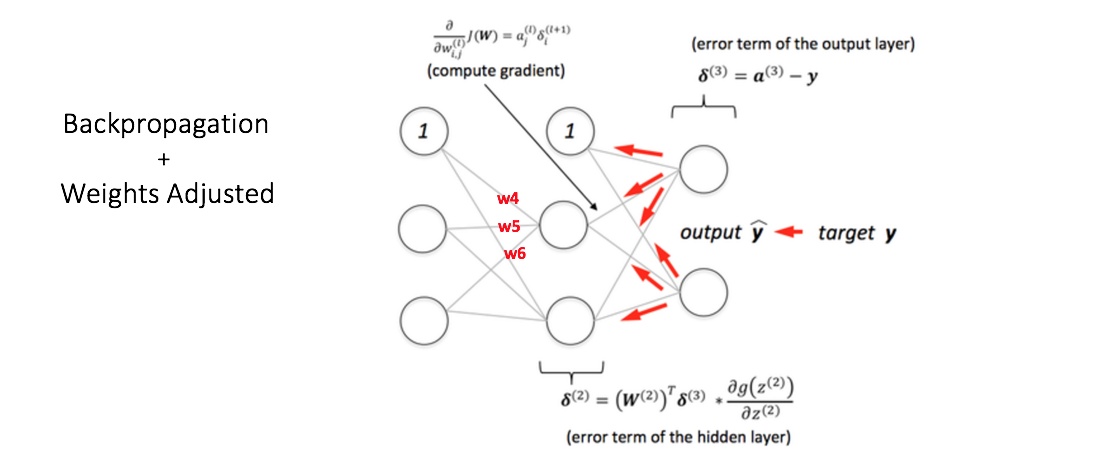
假设附给节点在反向传播和权重调整之后的新权重分别是 w4，w5 和 w6。接着用我们数据集中的其他训练样本来重复这一过程，不断迭代，这样，我们的网络就可以被视为学习了这些例子，从而使得输出误差不断减小，直到误差减小到一个合适的范围，那么我们就可以停止迭代了。这样我们就能够获得较为精准的预测模型。现在，如果我们想预测一个学习了 25 个小时、期中考试 70 分的学生是否能通过期末考试，我们可以通过前向传播步骤来计算 Pass 和 Fail 的输出概率。

过拟合与欠拟合

过拟合是指训练误差小，但是泛化误差较大；欠拟合是指训练误差大，泛化误差也很大。下面，我主要针对神经网络做一些相关的讨论
神经网络相比于其他的机器学习算法，其功能更为强大，只要给予神经网络足够多的节点，理论上它就能拟合任意的模型，但是也有缺点，就是容易产生过拟合。那么产生过拟合的根本原因是什么呢？那是因为我们并不能保证训练样本完全正确，也就是可能存在部分的样本存在误导性，所以当神经网络功能过于强大时，很容易连训练样本中的错误样本也学习了，从而导致只能具有很低训练误差，而不能拥有较低的泛化误差，也就是我们所说的过拟合。最常见的方法之一是提前终止学习，如图所示：

在合适的迭代次数终止算法从而达到最优容量（泛化误差最低)，但是最佳迭代次数并不好找，往往需要多次测试才有可能找到，因此更常用的方法是“Dropout”防止过拟合，下面来重点讲解：

Dropout

https://zhuanlan.zhihu.com/p/38200980

Dropout出现的原因

在机器学习的模型中，如果模型的参数太多，而训练样本又太少，训练出来的模型很容易产生过拟合的现象。在训练神经网络的时候经常会遇到过拟合的问题，过拟合具体表现在：模型在训练数据上损失函数较小，预测准确率较高；但是在测试数据上损失函数比较大，预测准确率较低。

过拟合是很多机器学习的通病。如果模型过拟合，那么得到的模型几乎不能用。为了解决过拟合问题，一般会采用模型集成的方法，即训练多个模型进行组合。此时，训练模型费时就成为一个很大的问题，不仅训练多个模型费时，测试多个模型也是很费时。

综上所述，训练深度神经网络的时候，总是会遇到两大缺点：

（1）容易过拟合

（2）费时

Dropout可以比较有效的缓解过拟合的发生，在一定程度上达到正则化的效果。

Dropout可以作为训练深度神经网络的一种trick供选择。在每个训练批次中，通过忽略一半的特征检测器（让一半的隐层节点值为0），可以明显地减少过拟合现象。这种方式可以减少特征检测器（隐层节点）间的相互作用，检测器相互作用是指某些检测器依赖其他检测器才能发挥作用。

Dropout说的简单一点就是：我们在前向传播的时候，让某个神经元的激活值以一定的概率p停止工作，这样可以使模型泛化性更强，因为它不会太依赖某些局部的特征，如图1所示。

图1：使用Dropout的神经网络模型

Dropout具体工作流程

假设我们要训练这样一个神经网络，如图2所示。

图2：标准的神经网络

输入是x输出是y，正常的流程是：我们首先把x通过网络前向传播，然后把误差反向传播以决定如何更新参数让网络进行学习。使用Dropout之后，过程变成如下：

（1）首先随机（临时）删掉网络中一半的隐藏神经元，输入输出神经元保持不变（图3中虚线为部分临时被删除的神经元）

图3：部分临时被删除的神经元

（2）然后把输入x通过修改后的网络前向传播，然后把得到的损失结果通过修改的网络反向传播。一小批训练样本执行完这个过程后，在没有被删除的神经元上按照随机梯度下降法更新对应的参数（w，b）。

（3）然后继续重复这一过程：

恢复被删掉的神经元（此时被删除的神经元保持原样，而没有被删除的神经元已经有所更新）
从隐藏层神经元中随机选择一个一半大小的子集临时删除掉（备份被删除神经元的参数）。
对一小批训练样本，先前向传播然后反向传播损失并根据随机梯度下降法更新参数（w，b）（没有被删除的那一部分参数得到更新，删除的神经元参数保持被删除前的结果）。

不断重复这一过程。

Dropout在神经网络中的使用

Dropout的具体工作流程上面已经详细的介绍过了，但是具体怎么让某些神经元以一定的概率停止工作（就是被删除掉）？代码层面如何实现呢？

下面，我们具体讲解一下Dropout代码层面的一些公式推导及代码实现思路。

（1）在训练模型阶段

无可避免的，在训练网络的每个单元都要添加一道概率流程。

图4：标准网络和带有Dropout网络的比较

对应的公式变化如下：
- 没有Dropout的网络计算公式：
- 采用Dropout的网络计算公式：
上面公式中Bernoulli函数是为了生成概率r向量，也就是随机生成一个0、1的向量。

代码层面实现让某个神经元以概率p停止工作，其实就是让它的激活函数值以概率p变为0。比如我们某一层网络神经元的个数为1000个，其激活函数输出值为y1、y2、y3、…、y1000，我们dropout比率选择0.4，那么这一层神经元经过dropout后，1000个神经元中会有大约400个的值被置为0。

*注意：* 经过上面屏蔽掉某些神经元，使其激活值为0以后，我们还需要对向量y1……y1000进行缩放，也就是乘以1/(1-p)。如果你在训练的时候，经过置0后，没有对y1……y1000进行缩放（rescale），那么在测试的时候，就需要对权重进行缩放，操作如下。

（2）在测试模型阶段

预测模型的时候，每一个神经单元的权重参数要乘以概率p。

图5：预测模型时Dropout的操作

为什么说Dropout可以解决过拟合？

（1）取平均的作用： 先回到标准的模型即没有dropout，我们用相同的训练数据去训练5个不同的神经网络，一般会得到5个不同的结果，此时我们可以采用 “5个结果取均值”或者“多数取胜的投票策略”去决定最终结果。例如3个网络判断结果为数字9,那么很有可能真正的结果就是数字9，其它两个网络给出了错误结果。这种“综合起来取平均”的策略通常可以有效防止过拟合问题。因为不同的网络可能产生不同的过拟合，取平均则有可能让一些“相反的”拟合互相抵消。dropout掉不同的隐藏神经元就类似在训练不同的网络，随机删掉一半隐藏神经元导致网络结构已经不同，整个dropout过程就相当于对很多个不同的神经网络取平均。而不同的网络产生不同的过拟合，一些互为“反向”的拟合相互抵消就可以达到整体上减少过拟合。

（2）减少神经元之间复杂的共适应关系： 因为dropout程序导致两个神经元不一定每次都在一个dropout网络中出现。这样权值的更新不再依赖于有固定关系的隐含节点的共同作用，阻止了某些特征仅仅在其它特定特征下才有效果的情况。迫使网络去学习更加鲁棒的特征，这些特征在其它的神经元的随机子集中也存在。换句话说假如我们的神经网络是在做出某种预测，它不应该对一些特定的线索片段太过敏感，即使丢失特定的线索，它也应该可以从众多其它线索中学习一些共同的特征。从这个角度看dropout就有点像L1，L2正则，减少权重使得网络对丢失特定神经元连接的鲁棒性提高。

（3）**Dropout类似于性别在生物进化中的角色：**物种为了生存往往会倾向于适应这种环境，环境突变则会导致物种难以做出及时反应，性别的出现可以繁衍出适应新环境的变种，有效的阻止过拟合，即避免环境改变时物种可能面临的灭绝。

Dropout在Keras中的源码分析

下面，我们来分析Keras中Dropout实现源码。

Keras开源项目GitHub地址为：

https://github.com/fchollet/keras/tree/master/keras

其中Dropout函数代码实现所在的文件地址：

https://github.com/fchollet/keras/blob/master/keras/backend/theano_backend.py

Dropout实现函数如下：

图6：Keras中实现Dropout功能

我们对keras中Dropout实现函数做一些修改，让dropout函数可以单独运行。

# coding:utf-8
import numpy as np

# dropout函数的实现
def dropout(x, level):
    if level < 0. or level >= 1: #level是概率值，必须在0~1之间
        raise ValueError('Dropout level must be in interval [0, 1[.')
    retain_prob = 1. - level

    # 我们通过binomial函数，生成与x一样的维数向量。binomial函数就像抛硬币一样，我们可以把每个神经元当做抛硬币一样
    # 硬币 正面的概率为p，n表示每个神经元试验的次数
    # 因为我们每个神经元只需要抛一次就可以了所以n=1，size参数是我们有多少个硬币。
    random_tensor = np.random.binomial(n=1, p=retain_prob, size=x.shape) #即将生成一个0、1分布的向量，0表示这个神经元被屏蔽，不工作了，也就是dropout了
    print(random_tensor)

    x *= random_tensor
    print(x)
    x /= retain_prob

    return x

#对dropout的测试，大家可以跑一下上面的函数，了解一个输入x向量，经过dropout的结果  
x=np.asarray([1,2,3,4,5,6,7,8,9,10],dtype=np.float32)
dropout(x,0.4)

out

[1 0 0 1 1 0 1 1 1 1]
[ 1.  0.  0.  4.  5.  0.  7.  8.  9. 10.]
Out[1]: 
array([ 1.6666666,  0.       ,  0.       ,  6.6666665,  8.333333 ,
        0.       , 11.666666 , 13.333333 , 14.999999 , 16.666666 ],
      dtype=float32)

函数中，x是本层网络的激活值。Level就是dropout就是每个神经元要被丢弃的概率。

*注意：* Keras中Dropout的实现，是屏蔽掉某些神经元，使其激活值为0以后，对激活值向量x1……x1000进行放大，也就是乘以1/(1-p)。

**思考：**上面我们介绍了两种方法进行Dropout的缩放，那么Dropout为什么需要进行缩放呢？

因为我们训练的时候会随机的丢弃一些神经元，但是预测的时候就没办法随机丢弃了。如果丢弃一些神经元，这会带来结果不稳定的问题，也就是给定一个测试数据，有时候输出a有时候输出b，结果不稳定，这是实际系统不能接受的，用户可能认为模型预测不准。那么一种”补偿“的方案就是每个神经元的权重都乘以一个p，这样在“总体上”使得测试数据和训练数据是大致一样的。比如一个神经元的输出是x，那么在训练的时候它有p的概率参与训练，(1-p)的概率丢弃，那么它输出的期望是px+(1-p)0=px。因此测试的时候把这个神经元的权重乘以p可以得到同样的期望。

总结：

当前Dropout被大量利用于全连接网络，而且一般认为设置为0.5或者0.3，而在卷积网络隐藏层中由于卷积自身的稀疏化以及稀疏化的ReLu函数的大量使用等原因，Dropout策略在卷积网络隐藏层中使用较少。总体而言，Dropout是一个超参，需要根据具体的网络、具体的应用领域进行尝试。