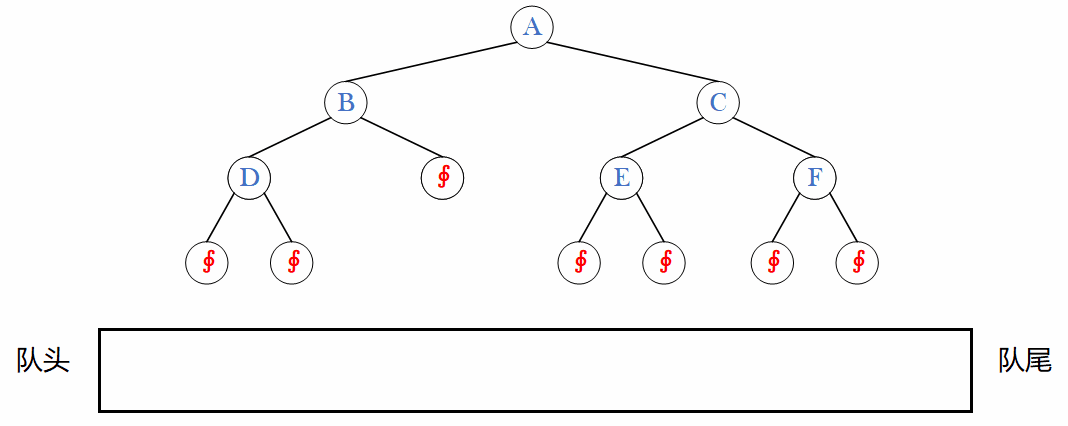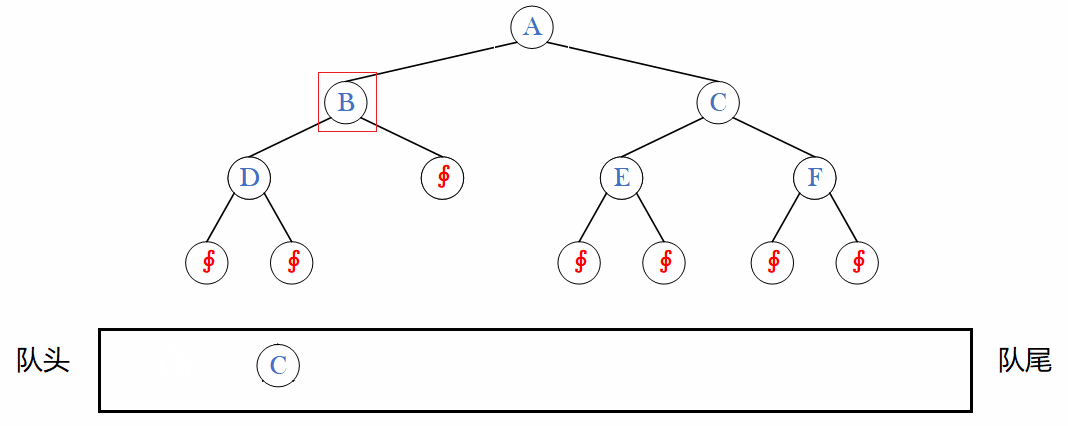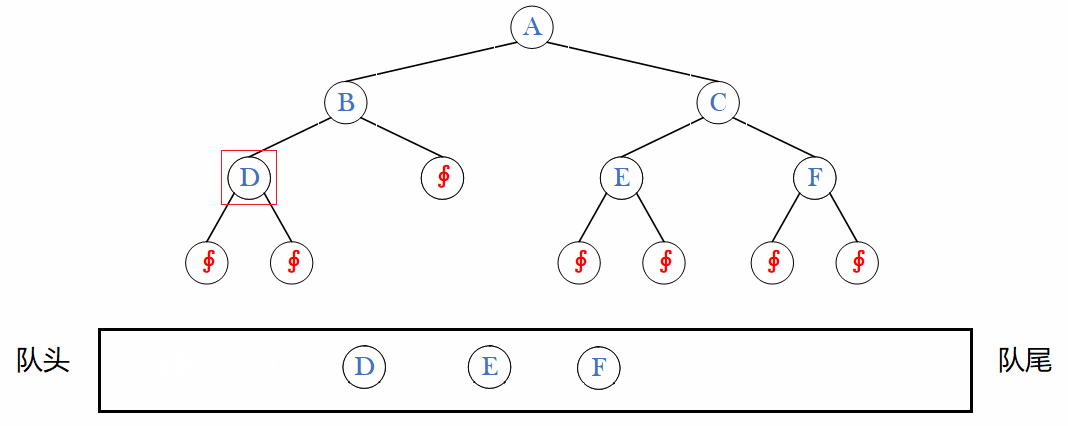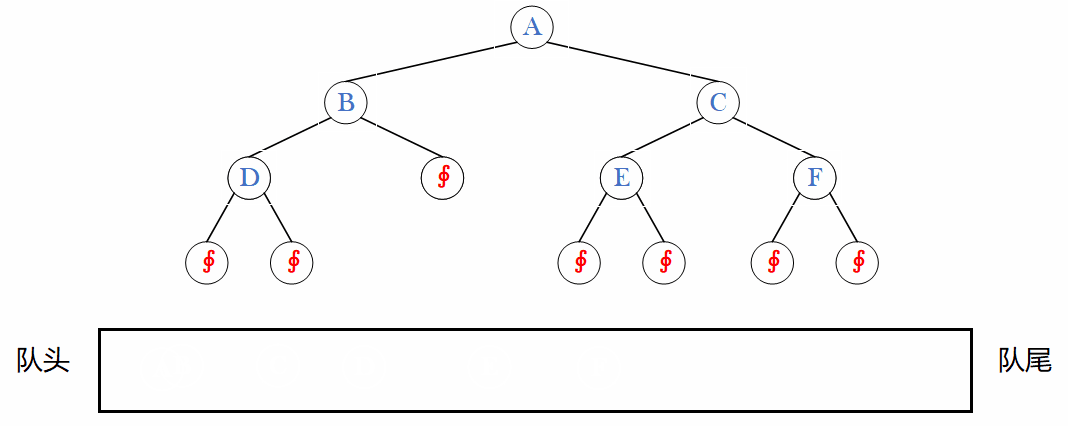
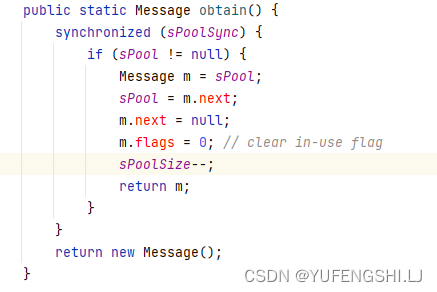
目录

多项式求值问题引入

什么是霍尔法则

---

多项式求值问题引入

题目链接：多项式求值

对于多项式求值问题，例如多项式:

常规的计算方法是每一项单独计算，即先计算，再接着计算，以此类推，最后求和即可，实现代码如下：

//其中n是多项式的阶数，a[]中存储系数，x是给定值。函数返回多项式f(x)的值
double f(int n, double a[], double x)
{
    double ans = 0;
    for (int i = 0; i <= n; i++)
    {
        ans += pow(x, i) * a[i];
    }

    return ans;
}

但是，上面的代码存在一些问题；

1. 性能可能较低，特别是在n较大时，因为pow(x, i)函数通常实现较为复杂，计算代价较高
2. 对于浮点运算，多次调用pow可能会引入数值稳定性问题

如果不是调用pow(x, i)函数计算，则还需要一层循环来单独计算的值，算法的时间复杂度为O()

//其中n是多项式的阶数，a[]中存储系数，x是给定值。函数返回多项式f(x)的值
double f( int n, double a[], double x ) {
    double ans = 0;
    for (int i = 0; i <= n; i++) {
        double temp = 1.0;
        
        for (int j = 0; j < i; j++) {
            temp *= x;
        }
        ans += a[i] * temp;
    }
    return ans;
}

所以为了减少多次的计算并且提高计算的准确性，可以考虑使用霍尔法则进行计算。

什么是霍尔法则

对于多项式的一般式来说：

可以简化为下面的等式：

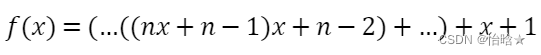
上面的等式即为霍尔法则

证明如下：

使用霍纳法则可以将上面的多项式转化成下面的形式：

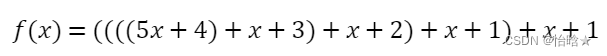
所以，使用霍尔算法优化后的代码即为：

//其中n是多项式的阶数，a[]中存储系数，x是给定值。函数返回多项式f(x)的值
double f(int n, double a[], double x)
{
    double ans = a[n];
    for (int i = n - 1; i >= 0; i--)
    {
        ans = ans * x + a[i];
    }
    return ans;
}

此时上面的代码时间复杂度只与多项式的阶数有关，而因为多项式的阶数为N，此时算法的时间复杂度即为O(N)