链表作为一个基础的数据结构,在开发中经常被使用。
链表往往使用如下的数据结构来表示,struct node 表示链表中的一个节点,data 表示节点的数据;next 表示这个节点指向的下一个节点,如果是链表的尾节点,那么 next 是空。
struct node {
int data;
struct node *next;
};在使用链表的时候,head 指针是需要维护的,head 是链表的头节点。在使用中,head 可以包含具体的数据,表示链表的第一个节点;head 也可以不包含数据,head->next 表示链表的第一个节点。
无论是链表的遍历,还是删除节点或者插入节点,关注的核心都是 next 指针。
链表相关的算法题,常见的解体思路有以下几个:
(1)链表翻转
(2)快慢指针
(3)递归算法
本文中记录了 leetcode 中和链表相关的几个题。
1 翻转链表
翻转链表
1.1 常规算法
下边这种算法,能兼容 head 是空的情况,如果 head 是空,那么 while() 循环就不会执行,返回 prev,也就是返回空。
ListNode* reverseList(ListNode* head) {
ListNode *prev = nullptr;
ListNode *cur = head;
while (cur) {
ListNode *tmp_next = cur->next;
cur->next = prev;
prev = cur;
cur = tmp_next;
}
return prev;
}1.2 递归算法
使用递归算法的数据结构有一个共同的特点,那就是在遍历数据的过程中,数据结构具有相似性。比如链表,向后遍历的过程中,从每一个节点开始也还都是一个链表;二叉树遍历的时候,也是使用递归算法,二叉树从每一个节点开始也都还是一棵二叉树。
class Solution {
public:
ListNode* reverseList(ListNode* head) {
return recursionReverse(head);
}
ListNode *recursionReverse(ListNode *head) {
// 递归退出条件
if (head == nullptr || head->next == nullptr) {
return head;
}
// 递归计算单元
ListNode *new_head = recursionReverse(head->next);
// 链表尾节点
// 维护指针, head->next 是 head 的写一个节点,
// 下一个节点指向 head
head->next->next = head;
// 翻转之后,head 成为了尾指针,所以 head 指向空
head->next = nullptr;
return new_head;
}
};2 链表排序
排序链表
排序算法中,数据往往保存在数组中,在数组中使用下标来访问数据比较方便。常见的排序算法,比如选择排序,插入排序,交换排序,快速排序,堆排序,归并排序。当数据保存在数组中的时候,这些算法都能够使用。但是当数据保存在链表中的时候,有些算法就不太好用了。
比如堆排序,堆的定义就是保存在数组中的完全二叉树,所以使用堆不合适。除非将数据移到数组中,使用堆排序排序之后再将数据移动到链表中。但是这样就失去了题目的意义。
链表适合使用归并排序。归并排序又分两类,第一类是基础的算法,段的长度从小到大进行逐级归并;第二种方法使用递归算法,从大到小进行递归。
使用递归算法,逻辑比较清晰,建议优先使用递归算法。
2.1 递归算法
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* sortList(ListNode* head) {
return mergeSort(head);
}
ListNode *mergeSort(ListNode *head) {
// 递归退出条件
if (head == nullptr) {
return head;
}
if (head->next == nullptr) {
return head;
}
// 使用快慢指针找到链表的中点
// 将链表分成两段,进行递归运算
ListNode *slow_prev = nullptr;
ListNode *slow = head;
ListNode *fast = head;
while (fast && fast->next) {
slow_prev = slow;
slow = slow->next;
fast = fast->next->next;
}
// slow_prev 表示第一段的尾节点
// 将尾节点的 next 设置为空,便于判断链表是不是遍历完毕
if (slow_prev) {
slow_prev->next = nullptr;
}
// 将两段链表分别进行递归排序,
// 返回排序之后的 head
ListNode *head1 = mergeSort(head);
ListNode *head2 = mergeSort(slow);
// 将排好序的链表进行合并
ListNode *tmp1 = head1;
ListNode *tmp2 = head2;
ListNode *ret_head_prev = new ListNode(0, nullptr);
ListNode *tmp_tail = ret_head_prev;
while (tmp1 && tmp2) {
if (tmp1->val < tmp2->val) {
tmp_tail->next = tmp1;
tmp1 = tmp1->next;
} else {
tmp_tail->next = tmp2;
tmp2 = tmp2->next;
}
tmp_tail = tmp_tail->next;
}
if (tmp1) {
tmp_tail->next = tmp1;
}
if (tmp2) {
tmp_tail->next = tmp2;
}
ListNode *ret = ret_head_prev->next;
delete ret_head_prev;
return ret;
}
public:
ListNode *ret = nullptr;
};2.2 常规算法
① 将相邻的两段进行排序合并
② 段的长度从 1 开始
第一次合并时相邻的两个数排序合并,1900, 300 合并之后是 300, 1900; 1500, 900 合并之后是 900, 1500;以此类推。
第二次合并的段的长度是 2,有第一次做基础,长度是 2 的段是排好序的。300, 1900, 900, 1500 归并之后是 300, 900, 1500, 1900以此类推。
...
合并到最后,段的长度大于等于数据的长度便会停止合并。
每次归并排序,段的长度是上次段长度的二倍,因为每一次排序都建立在上一次排序的基础之上,所以本次排序的段的长度是上一次排序的段的长度的二倍。
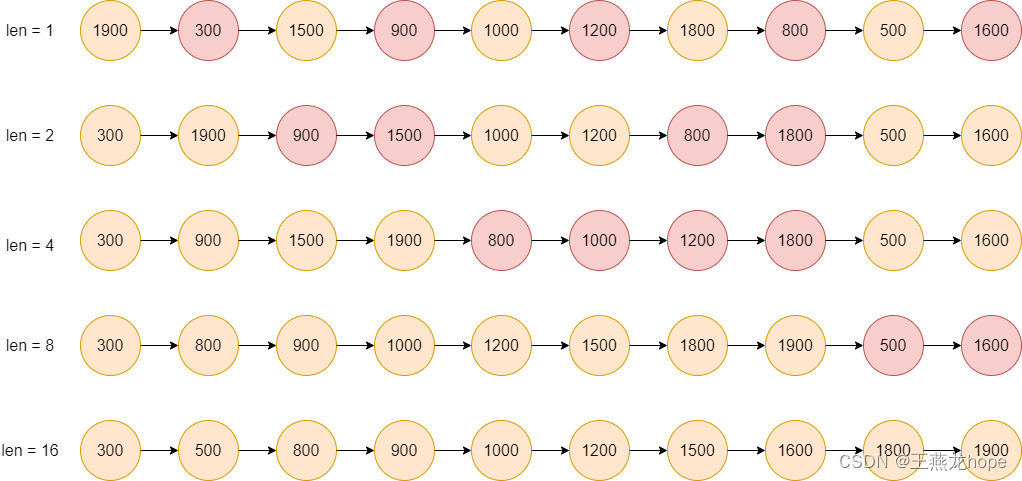
使用这种方式进行归并的时候,需要维护的指针比较多,稍不注意,就很容易出错。
以 len = 2 这一步为例:
① 首先需要找到第二段的头指针,这就需要使用当前的 head 向后移动 2 个位置
② 当 len = 2 的这两段合并之后,需要和上一次 len = 2 两段合并的结果进行连接,所以需要维护上一次合并之后的尾指针
③ 当这两段合并完成之后,下一次要合并后边的两段,所以在这次合并之前就需要找到下次合并的头指针
不仅仅要关注与当前在关心的这两段,上次已经合并的尾指针以及下次要合并的头指针,也都要维护。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* sortList(ListNode* head) {
if (head == nullptr || head->next == nullptr) {
return head;
}
return mergeSort(head);
}
ListNode *mergeSort(ListNode *head) {
ListNode *ret_head = head;
// 计算链表的长度
int list_len = getListLen(head);
// 遍历段的长度,从 1 开始,到大于等于链表的长度的时候停止
for (int i = 1; i < list_len; i *= 2) {
// 返回的 head 是不是已经赋值了
bool head_set = false;
ListNode *last_tail = nullptr;
ListNode *tmp_head = ret_head;
// 两层循环
// 第一层循环是遍历段的长度
// 第二层循环是使用这个段的长度将数据切割,相邻的两段进行合并
while (tmp_head) {
// 第一段的头节点
ListNode *first = tmp_head;
// second 表示第二段的头节点
// 后边通过移动来指向第二段的头节点
ListNode *second = tmp_head;
ListNode *first_tail = nullptr;
ListNode *second_tail = nullptr;
// 段的长度是 i
// 通过 second 向后移动找到第二段链表的头指针
int j = 0;
for (j = 0; j < i; j++) {
if (second) {
first_tail = second;
second = second->next;
} else {
break;
}
}
// j < i,说明没有找到第二段的头指针的时候链表就结束了
// 这个时候数据的数量小于等于一段,不需要归并
if (j < i) {
break;
}
// 将第一段的尾指针指向空
first_tail->next = nullptr;
// 找到第二段的段尾,然后段尾尾指向空
// second_tail 是第二段的断尾
// tmp_second 是第二段的断尾的下一个节点
ListNode *tmp_second = second;
j = 0;
for (j = 0; j < i; j++) {
if (tmp_second) {
second_tail = tmp_second;
tmp_second = tmp_second->next;
} else {
break;
}
}
if (second_tail) {
second_tail->next = nullptr;
}
// 将两段合并
ListNode *tmp_ret = mergeTwoSection(first, second);
// 设置 head
if (head_set == false) {
ret_head = tmp_ret;
head_set = true;
}
// 相邻两次合并的两段进行连接
if (last_tail == nullptr) {
while (tmp_ret->next) {
tmp_ret = tmp_ret->next;
}
last_tail = tmp_ret;
} else {
last_tail->next = tmp_ret;
while (last_tail->next) {
last_tail = last_tail->next;
}
}
// 将合并好的这段和链表剩余的节点进行连接
// 这样即使剩余的节点个数小于等于一段的节点个数,直接退出循环,也保证了链表是连接的
last_tail->next = tmp_second;
tmp_head = tmp_second;
}
}
return ret_head;
}
int getListLen(ListNode *head) {
int len = 0;
while (head) {
len++;
head = head->next;
}
return len;
}
ListNode *mergeTwoSection(ListNode *first, ListNode *second) {
// 假的链表头
// ret_head_prev->next 是最终要返回的链表头
ListNode *ret_head_prev = new ListNode(0, nullptr);
// 维护链表的尾节点
// 在排序过程中,节点追加到尾部
ListNode *tmp_tail = ret_head_prev;
ListNode *tmp_first = first;
ListNode *tmp_second = second;
while (tmp_first && tmp_second) {
if (tmp_first->val > tmp_second->val) {
tmp_tail->next = tmp_second;
tmp_second = tmp_second->next;
} else {
tmp_tail->next = tmp_first;
tmp_first = tmp_first->next;
}
tmp_tail = tmp_tail->next;
}
if (tmp_first) {
tmp_tail->next = tmp_first;
} else if (tmp_second) {
tmp_tail->next = tmp_second;
}
ListNode *ret = ret_head_prev->next;
return ret;
}
};3 有环链表
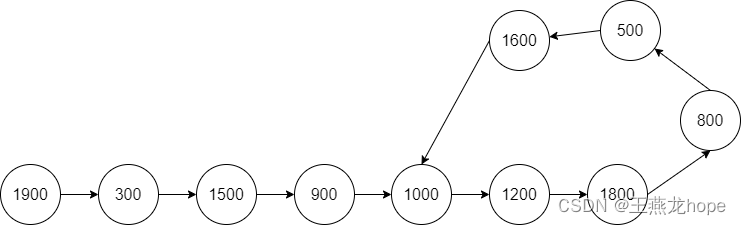
环形链表
存在环的链表,如下图所示。当链表中没有环的时候,遍历链表的时候可以通过 next 指针是不是空来判断是不是遍历到了链表的结尾;当链表中存在环的时候,就不能使用这种方式来判断链表的结尾了。
有环链表常见的问题有 3 个:
(1)判断链表中有没有环
(2)如果有环的话,找到环的入口节点
(3)计算环的长度
3.1 借助 map
遍历链表,每遍历一个节点就将链表节点放到 map 中,在放 map 之前先判断节点在 map 中是不是存在,如果存在说明存在环,并且这个 map 中已经存在的节点就是环的入口节点。
将节点加入到 map 中的时候,key 是链表节点的地址,value 表示这个节点是遍历的第几个节点,也就是遍历节点的序号。当第一次遍历到节点重复时,两个节点的序号差就是环的长度。
借助于 map 这种方式,逻辑清晰,好理解。
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
std::map<ListNode *, int> node_map;
int index = 0;
while (head) {
if (node_map.count(head) > 0) {
// map 中已经存在这个节点, 说明链表中有环
std::cout << "cycle len: " << index - node_map[head] << std::endl;
return head;
} else {
// 将节点放入 map,value 是遍历到这个节点的序号
// 第一个遍历的节点序号是 0,第二个遍历的节点序号是 1,以此类推
node_map[head] = index;
index++;
}
head = head->next;
}
return nullptr;
}3.2 快慢指针
3.2.1 判断有没有环
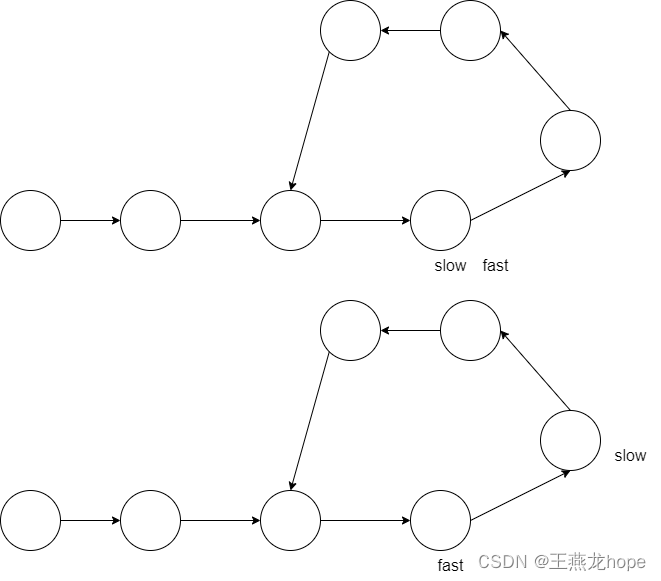
慢指针和快指针同时从链表的头节点出发,慢指针一次移动一个节点,快指针一次移动两个节点。如果两个节点能够相遇,说明链表中有环。
链表中有环,慢指针和快指针就一定会相遇吗 ?
答案是肯定的。
如下图所示,分 3 种情况来讨论:
(1)在快慢指针移动过程中,两个指针重合了
(2)slow 和 fast 相差一个节点,slow 在前
再移动一次,slow 和 fast 就会重合
还有其他情况,比如 slow 和 fast 相差比较远的情况。对于这些情况,经过一定次数的移动之后,最终情况就会归结到这 2 种情况。
3.2.2 环的入口节点
当 slow 和 fast 相遇的时候,新增一个指针,从链表的 head 开始,起名为 tmp。tmp 从 head 出发,slow 从相遇节点出发,两个节点每次移动一个节点。当 tmp 和 head 相遇的时候,那么这个相遇点就是环的入口节点。
至于为什么会有这样的规律,可以参考 leet 官方题解:
https://leetcode.cn/problems/c32eOV/solutions/1037744/lian-biao-zhong-huan-de-ru-kou-jie-dian-vvofe/
3.2.3 环的长度
当 slow 和 fast 相遇时,保持 fast 不动,移动 slow,记录 slow 移动的节点数,到下次 slow 和 fast 相遇时,slow 移动的节点数就是环的长度。
4 两个链表的第一个公共节点
两个链表的第一个公共节点
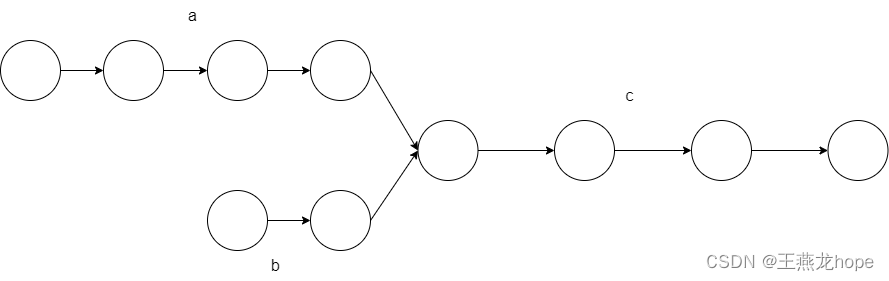
如下图所示,两个链表从某一个节点开始时重合的,这样的链表也称 Y 形链表。
4.1 算法一
先计算出两个链表的长度,比如两个链表分别是 list1 和 list2,长度分别是 len1 和 len2,并且 len1 > len2,计算出 len1 和 len2 的差值是 d。
算法可以分为两步:
(1)先遍历 list1,遍历节点个数是 d,遍历 d 个节点之后,list1 和 list2 是对齐的
(2)再同时遍历 list1 和 list2,在遍历过程中比较两个节点的地址是不是相同,相同则直接返回,不相同则继续遍历
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
int len1 = getListLength(headA);
int len2 = getListLength(headB);
int distance = 0;
struct ListNode *tmp1 = headA;
struct ListNode *tmp2 = headB;
if (len1 > len2) {
distance = len1 - len2;
for (int i = 0; i < distance; i++) {
tmp1 = tmp1->next;
}
} else {
distance = len2 - len1;
for (int i = 0; i < distance; i++) {
tmp2 = tmp2->next;
}
}
while (tmp1 && tmp2) {
if (tmp1 == tmp2) {
return tmp1;
}
tmp1 = tmp1->next;
tmp2 = tmp2->next;
}
return NULL;
}
int getListLength(struct ListNode *head) {
int len = 0;
while (head) {
len++;
head = head->next;
}
return len;
}
};4.2 算法二
从上边这张图中可以看出来,两个链表重合的部分长度是 c,不重合的部分长度分别是 a 和 b。list1 的长度是 a + c,list2 的长度是 b + c。
从两个链表分别开始遍历,list1 遍历结束,跳到 list2 进行遍历;list2 遍历结束,跳到 list1 开始遍历。这两个遍历路径遍历的长度分别是 a + c + b 和 b + c + a,两个长度是相等的。这样也可以找到两个链表相交的第一个节点。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
ListNode *tmp_a = headA;
ListNode *tmp_b = headB;
while (tmp_a != tmp_b) {
if (tmp_a == nullptr) {
tmp_a = headB;
} else {
tmp_a = tmp_a->next;
}
if (tmp_b == nullptr) {
tmp_b = headA;
} else {
tmp_b = tmp_b->next;
}
}
return tmp_a;
}
};5 k 个一组反转链表
k 个一组翻转链表
5.1 递归算法
对于链表的题目,如果使用常规方法,那么需要维护链表的好几个段,要维护多个指针,从上边的链表排序也可以看出来。使用常规方法的时候,需要特别小心,很容易出错。
这个题目,可以使用递归的方式。使用递归的方式,可以减少链表节点的维护,降低复杂度;但是要注意递归的退出条件,不能有遗漏。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverseKGroup(ListNode* head, int k) {
return reverseKGroupHelper(head, k);
}
ListNode *reverseKGroupHelper(ListNode *head, int k) {
// 如果链表为空,直接返回
if (head == nullptr) {
return head;
}
// 遍历链表,看看链表节点够不够 k 个
ListNode *this_section_tail = head;
int i = 0;
for (i = 0; i < k - 1 ; i++) {
if (this_section_tail) {
this_section_tail = this_section_tail->next;
} else {
break;
}
}
// 如果链表的长度不足 k,直接返回
// 为什么有第二个条件呢,
// 因为即使 i 和 k - 1 是相等的,那么也可能存在 this_section_tail 是空的情况
if (i < k - 1 || this_section_tail == nullptr) {
return head;
}
// 下一段的头节点
ListNode *next_section_head = this_section_tail->next;
this_section_tail->next = nullptr;
ListNode *reversed_head = reverseList(head);
ListNode *reversed_group_head = reverseKGroupHelper(next_section_head, k);
head->next = reversed_group_head;
return reversed_head;
}
ListNode *reverseList(ListNode *head) {
ListNode *prev = nullptr;
ListNode *curr = head;
while (curr) {
ListNode *tmp_next = curr->next;
curr->next = prev;
prev = curr;
curr = tmp_next;
}
return prev;
}
};5.2 常规算法
建议优先选择递归算法。常规算法需要维护的节点较多,上一次翻转之后的尾节点,这次翻转前后的头节点和尾节点,下一段的头节点。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverseKGroup(ListNode* head, int k) {
// 表示当前遍历到哪个节点了
ListNode *tmp_head = head;
// 上一段翻转之后的尾
ListNode *prev_tail_after_reverse = nullptr;
// 当前要翻转的这段的头和尾
ListNode *curr_section_head = head;
ListNode *curr_section_tail = nullptr;
// 下一段的头
ListNode *next_section_head = nullptr;
ListNode *ret = nullptr;
int len = 0;
while (tmp_head) {
// 记录节点的个数,达到 k 个,会进行翻转
len++;
if (len == k) {
// 维护一些节点
// 下一次从这个节点开始遍历,也是下一次要翻转的链表段的头节点
ListNode *tmp_head_next = tmp_head->next;
// 当前这一段的尾节点,翻转之前的尾节点
curr_section_tail = tmp_head;
// 下一次要翻转的段的头节点
next_section_head = curr_section_tail->next;
// 将这一段的尾节点的 next 置空
curr_section_tail->next = nullptr;
// 将这段链表进行翻转,返回的是翻转之后的头节点
ListNode *tmp_section_head = reverseList(curr_section_head);
// 第一段翻转的头节点,就是返回值
if (ret == nullptr) {
ret = tmp_section_head;
}
if (prev_tail_after_reverse) {
prev_tail_after_reverse->next = tmp_section_head;
}
prev_tail_after_reverse = curr_section_head;
// 将这一段与下一段连接
curr_section_head->next = next_section_head;
curr_section_head = next_section_head;
curr_section_tail = nullptr;
len = 0;
tmp_head = tmp_head_next;
continue;
}
tmp_head = tmp_head->next;
}
return ret == nullptr ? head : ret;
}
ListNode *reverseList(ListNode *head) {
ListNode *prev = nullptr;
ListNode *curr = head;
while (curr) {
ListNode *tmp_next = curr->next;
curr->next = prev;
prev = curr;
curr = tmp_next;
}
return prev;
}
};6 链表回文串
回文链表
leetcode 官方题解中给出了 3 中解决方法:
(1)将链表中的数据拷贝到数组中,然后使用双指针进行判断
(2)使用快慢指针
首先找到链表的中间节点,然后将后半段的节点进行翻转,翻转之后就可以遍历两段链表进行比较判断。最后还要将翻转的链表恢复原样。
(3)递归算法
如下是递归算法的代码:
也是两个节点尽心比较,左边的节点用 first 表示,右边的节点是 head。在递归的过程中 first 向右移动,head 向左移动。递归算法,归去来兮。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
bool isPalindrome(ListNode* head) {
first_ = head;
isPalindromeHelper(head);
return result_;
}
void isPalindromeHelper(ListNode *head) {
if (head == nullptr) {
return;
}
if (result_ == false) {
return;
}
if (head->next != nullptr) {
isPalindromeHelper(head->next);
}
int val_a = first_->val;
int val_b = head->val;
if (val_a != val_b) {
result_ = false;
return;
}
first_ = first_->next;
}
private:
bool result_ = true;
ListNode *first_ = nullptr;
};


![[软件工具]批量根据文件名查找PDF文件复制到指定的地方,如何批量查找文件复制,多个文件一起查找复制](https://img-blog.csdnimg.cn/img_convert/692bd908f35322a9272095f8fd0df5d0.webp?x-oss-process=image/format,png)