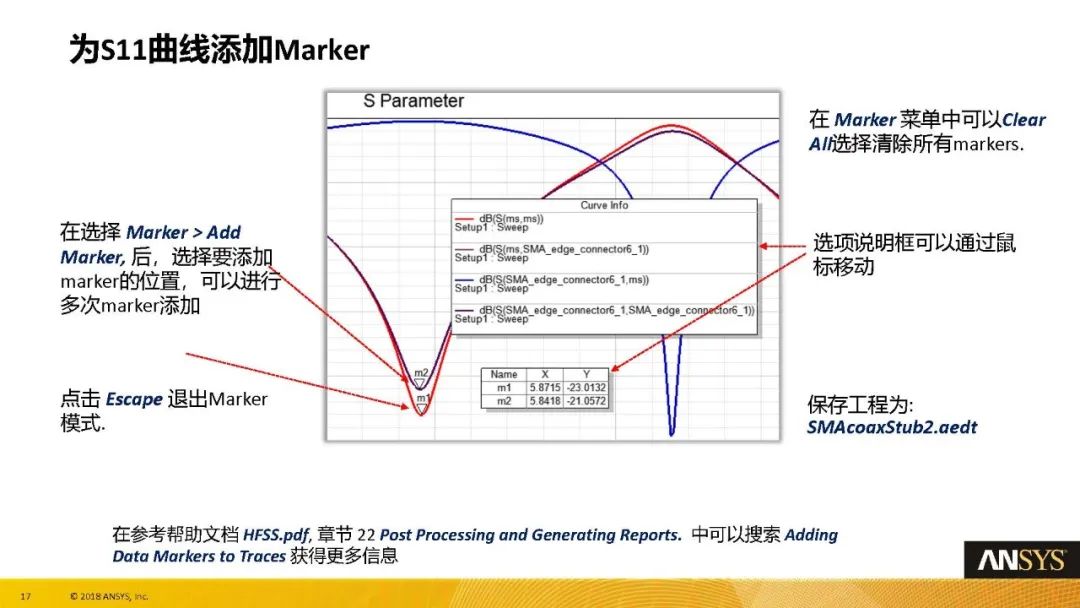
图论不同地方讲的不太一样,本文仅限作者的理解
定义
图是一般由点集
V
V
V 和边集
E
E
E 组成。
对于
v
∈
V
v\in V
v∈V,称
v
v
v 为该图的一个节点。
对于
e
∈
E
e\in E
e∈E,一般用二元组
(
u
,
v
)
(u,v)
(u,v) 表示
e
e
e,其中
u
,
v
∈
V
u,v\in V
u,v∈V。在无向图中,该二元组无序,即边为双向;在有向图中,该二元组有序,即边为单向。
一个带有边权(边的长度)的图称为带权图,此时边一般记为
(
u
,
v
,
w
)
(u,v,w)
(u,v,w)。
下面分别是一个无向图和一个有向图的例子:


连通性
从一个图中选出一些节点和边,构成一个合法的新图,称做原图的子图。
扩展至最大的符合某一要求的子图被称为分量。
通过图中的边可以使节点之间联通(单向联通也算)的图称做连通图。
节点之间两两可以互相到达的有向图被称做强联通图。
如果一个图中某一个点及其边被删去后,图将不再联通,则称该点为原图的一个割点。
没有割点的图被称为点双连通图。
如果一个图中某一条边被删去后,图将不再联通,则称该边为原图的一个割边。
没有割边的图被称为边双连通图。
读者可以自行理解联通子图、联通分量、强连通子图、强连通分量、点双联通子图、点双联通分量、边双联通子图、边双联通分量等概念。
树与环
一个没有环的图称为无环图。
一个没有环的有向图称为有向无环图(DAG)。
一个没有环且联通的无向图称为树。
一个有恰一个环且联通的无向图称为基环树。
一个是树且包含所有节点的子图称为原图的生成树。
存储
一般有两种存储方式,邻接矩阵和邻接表。
邻接矩阵
使用一个矩阵来存储图,对于矩阵中的一个元素
G
u
,
v
G_{u,v}
Gu,v:
在无权图中,
u
,
v
u,v
u,v 之间有边为
1
1
1,无边为
0
0
0;
在带权图中,
u
,
v
u,v
u,v 之间有边为
w
w
w,无边为
inf
\inf
inf。
邻接表
使用多个数组来存储图,对于每一个数组
G
u
G_u
Gu
在无权图中,
u
,
v
u,v
u,v 间有边则加入
v
v
v;
在带权图中,
u
,
v
u,v
u,v 间有边则加入有序二元组
(
v
,
w
)
(v,w)
(v,w)。
代码
分为定义,输入和遍历三部分
- 邻接矩阵
int G[N][N];
memset(G,0,sizeof(G));//无权
memset(G,INF,sizeof(G));//带权
for (int i=1;i<=m;i++){
//无权
int u,v;
cin>>u>>v;
G[u][v]=1;
G[v][u]=1;//仅限无向图
//带权
int u,v,w;
cin>>u>>v>>w;
G[u][v]=w;
G[v][u]=w;//仅限无向图
}
for (int u=1;u<=n;u++) for (int v=1;v<=n;v++)
if (G[u][v])//无权
if (G{u][v]!=INF)//带权
- 邻接表
vector<int> G[N];//无权
//带权
struct edge{int v,w;};
vector<edge> G[N];
for (int i=1;i<=m;i++){
//无权
int u,v;
cin>>u>>v;
G[u].push_back(v);
G[v].push_back(u);//仅限无向图
//带权
int u,v,w;
cin>>u>>v>>w;
G[u].push_back({v,w});
G[v].push_back({u,w});//仅限无向图
}
for (int u=1;u<=n;u++)
for (int v:G[u])//无权
for (edge e:G[u])//带权