一、单项选择(共 15 题,每题 2 分,共计 30 分,每题有且仅有一个正确选项)
以下是题目和解析的完整格式:
- 不可以作为c++中的变量名的是( )。
- A. I以下loveChina
- B. I_loveChina
- C. I_love_China
- D. i_loveChina
正确答案:A. I以下loveChina
解析:
- 在C++中,变量名命名需要遵循一定的规则。变量名可以由字母、数字和下划线组成,但是第一个字符不能是数字。
- 此外,变量名中不能包含空格和其他特殊字符(下划线除外)。
- 选项A中的变量名包含了空格,不符合C++变量命名规则,因此不可以作为C++中的变量名。
- 选项B、C、D的变量名都符合C++的命名规则,可以作为合法的变量名。
- 在体育课上,N(N>0 且是 3 的倍数)位同学要分成三人一组来打篮球,规则如下:
同学们按照衣服上的编号从 1 到 N 的顺序站成一队,从第一位同学开始,每三位同学为一队,其中三位同学中编号最小的为队长。例如编号为 1,2,3 的同学为一队,并且编号为 1 同学为队长。输入一个数字 N,来判断这个同学是不是队长。要实现这个功能,应该在横线处写的代码为( )。
1. int n; 2. cin >> n; 3. if(_____){ 4. cout <<"是队长"; 5. }else{ 6. cout <<"不是队长"; 7. }
- A. n%2==1
- B. n%3==0
- C. (n-1)/3==1
- D. (n-1)%3==0
正确答案:D. (n-1)%3==0
解析:
- 根据题目描述,每三位同学为一队,编号最小的同学为队长。因此,队长的编号应该是1、4、7、10…,即队长的编号满足(编号-1)是3的倍数。
- 在代码中,n代表同学的编号,如果(n-1)%3==0成立,说明(n-1)是3的倍数,那么这个编号的同学就是队长。
- 选项A的条件n%2==1判断n是否为奇数,与题目要求不符。
- 选项B的条件n%3==0判断n是否为3的倍数,但并不是每个3的倍数都是队长编号。
- 选项C的条件(n-1)/3==1只有在n=4时才成立,不能适用于所有队长编号的判断。
- 因此,正确答案是选项D。
- 定义一个double类型的变量,下面定义不合法的是( )。
- A. double a = 3.14;
- B. double a = (double)3.14;
- C. double a = (double)(3.14);
- D. double a = double 3.14;
正确答案:D. double a = double 3.14;
解析:
- 在C++中,定义double类型变量可以直接赋值一个小数,如选项A所示。
- 也可以使用强制类型转换(double)将一个数值转换为double类型,如选项B和C所示。其中,选项C的两层括号是多余的,但并不影响其合法性。
- 选项D的写法是错误的,double不能像int、short等类型那样放在数值前作为类型转换,正确的写法应该是
double a = (double)3.14;或者double a = static_cast<double>(3.14);。 - 因此,选项D的定义方式是不合法的。
- 执行下列c++代码,输出的是( )。
1. int x = 5,sum=0; 2. for(int i=1;i<6;i++){ 3. sum += (x - i) * (x - i); 4. } 5. cout << sum;
- A. 30
- B. 31
- C. 16
- D. 18
正确答案:A. 30
解析:
- 首先定义了变量x的值为5,sum的初始值为0。
- 然后进入for循环,循环变量i从1到5,执行5次循环。
- 在每次循环中,计算(x - i) * (x - i)的值,并将结果累加到sum中。
- 当i=1时,(x - i) * (x - i) = (5 - 1) * (5 - 1) = 4 * 4 = 16,sum = 0 + 16 = 16
- 当i=2时,(x - i) * (x - i) = (5 - 2) * (5 - 2) = 3 * 3 = 9,sum = 16 + 9 = 25
- 当i=3时,(x - i) * (x - i) = (5 - 3) * (5 - 3) = 2 * 2 = 4,sum = 25 + 4 = 29
- 当i=4时,(x - i) * (x - i) = (5 - 4) * (5 - 4) = 1 * 1 = 1,sum = 29 + 1 = 30
- 当i=5时,(x - i) * (x - i) = (5 - 5) * (5 - 5) = 0 * 0 = 0,sum = 30 + 0 = 30
- 循环结束后,sum的值为16 + 9 + 4 + 1 + 0 = 30。
- 最后输出sum的值30,即为选项A。
- 下面是小红同学一周的课余时间安排,当输入5时,将会输出( )。
1. int n; 2. cin >> n; 3. switch(n){ 4. case 1: cout << "写作业 " ; break; 5. case 2: 6. case 3: cout << "学游泳 " ; break; 7. case 4: 8. case 5: 9. case 6: cout << "弹钢琴 " ; 10. case 7: cout << "睡觉 " ; 11. }
- A. 什么也不会输出
- B. 弹钢琴 睡觉
- C. 弹钢琴
- D. 以上都不对
正确答案: B. 弹钢琴 睡觉
解析:
- 这段代码使用了switch语句,根据输入的n值来决定输出内容。
- 当n为1时,输出"写作业",并通过break跳出switch语句。
- 当n为2或3时,输出"学游泳",并通过break跳出switch语句。
- 当n为4、5、6时,会依次执行case 4、case 5、case 6的代码,由于没有break语句,会一直执行直到遇到break或switch结束。
- 当n为7时,输出"睡觉"。
- 当输入为5时,会匹配到case 5,但是由于没有break,会继续执行case 6和case 7的代码,最终输出"弹钢琴 睡觉"。
- 因此,当输入为5时,正确的输出是"弹钢琴 睡觉",对应选项B。
- 小华是一名设计师,他正在为一个客户设计一个网站。客户要求网站的主颜色必须是特定的蓝色,并提供了这个颜色的RGB值:(0, 105, 211)。为了在网站的CSS代码中使用这个颜色,小华需要将RGB值转换为十六进制表示。他知道,在十六进制表示中,每种颜色(红、绿、蓝)都用两位数字表示,范围从00到FF。请你帮小华计算下(0,105,211)对应的的16进制表示是( )。
- A. #00105211
- B. #0069D3
- C. #0066DD
- D. #0066D2
正确答案: B. #0069D3
解析:
- 在CSS中,颜色可以使用RGB值或十六进制值表示。十六进制值以"#"开头,后面跟着6位十六进制数字,每两位代表一种颜色(红、绿、蓝)的强度。
- 十六进制数字的范围是0到9以及A到F,其中A到F对应十进制的10到15。
- 要将RGB值(0, 105, 211)转换为十六进制表示,需要将每个颜色分量转换为两位十六进制数:
- 红色®:0 -> 00 (十六进制)
- 绿色(G):105 -> 69 (十六进制)
- 短除法计算过程:
- 105 ÷ 16 = 6 余 9
- 9对应十六进制的9
- 6对应十六进制的6
- 从下往上读,105对应的十六进制表示为69
- 短除法计算过程:
- 蓝色(B):211 -> D3 (十六进制)
- 短除法计算过程:
- 211 ÷ 16 = 13 余 3
- 3对应十六进制的3
- 13对应十六进制的D
- 从下往上读,211对应的十六进制表示为D3
- 短除法计算过程:
- 将转换后的六位十六进制数组合在一起,并在前面加上"#",得到完整的十六进制颜色值:#0069D3。
- 因此,选项B是正确的十六进制表示。
- 下列流程图输出结果是( )。
- A. 2
- B. 1
- C. 3
- D. 12
正确答案:A. 2
解析:
- 根据流程图,我们可以分析出这是一个循环的过程,初始值
x = 21,cnt = 0。 - 然后进入循环条件判断
x > 0:- 第一次循环:
x = 21 > 0成立,进入循环体- 执行
x = x / 10,此时x = 21 / 10 = 2.1,由于x是整型,所以x = 2 - 执行
cnt = cnt + 1,此时cnt = 0 + 1 = 1
- 第二次循环:
x = 2 > 0成立,进入循环体- 执行
x = x / 10,此时x = 2 / 10 = 0.2,由于x是整型,所以x = 0 - 执行
cnt = cnt + 1,此时cnt = 1 + 1 = 2
- 第三次循环:
x = 0 > 0不成立,跳出循环
- 第一次循环:
- 跳出循环后,执行输出
cnt的值,此时cnt = 2。 - 因此,流程图的输出结果是2,对应选项A。
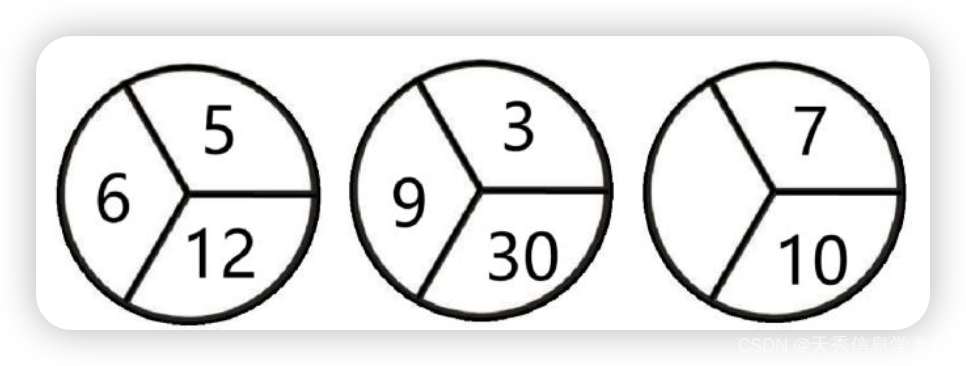
- 根据前两个图形中数字的规律,第三个图形的空白处应该填( )。
- A. 7
- B. 10
- C. 12
- D. 6
解析:
官方答案为A,规律有待考量
非常抱歉,我误解了您的要求。现在我将在解析中为您绘制图示,以更清晰地展示兔子数量的变化规律。
- 如图分别为1到4月的兔子情况,假设一对小兔子要一个月才到成熟期(可以生小兔子的时期),而一对成熟兔子每月会生一对小兔子。如果第一个月时只有一对成熟兔子,7个月时会有( )对小兔子。
- A. 15
- B. 8
- C. 12
- D. 5
正确答案: B. 8
解析:
-
根据题目描述,我们可以得到以下信息:
- 第一个月有1对成熟兔子;
- 小兔子需要一个月才能成熟;
- 每对成熟兔子每月会生一对小兔子。
-
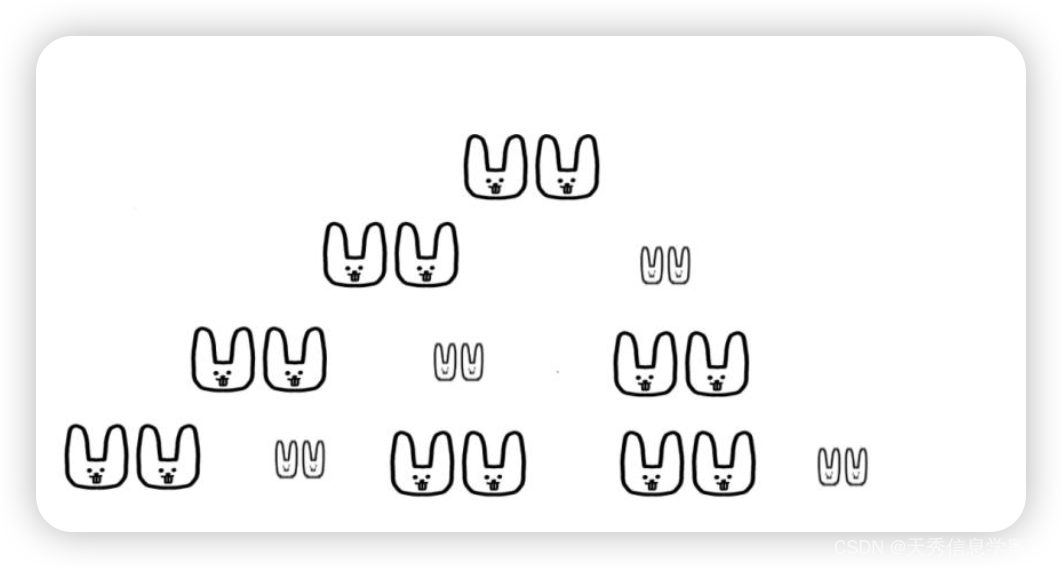
根据这些信息,我们可以绘制出前7个月兔子数量的变化图示(大表示成兔,小表示小兔):
-
从图示中我们可以看出,每个月的小兔子数量变化规律如下:
- 第1个月: 0对小兔子
- 第2个月: 1对小兔子
- 第3个月: 1对小兔子
- 第4个月: 2对小兔子
- 第5个月: 3对小兔子
- 第6个月: 5对小兔子
- 第7个月: 8对小兔子
-
因此,第7个月会有8对小兔子,对应选项B。
通过这种图示方式,我们可以清晰地看到每个月成兔和小兔的数量变化。每个月的总兔子数量等于前两个月的总兔子数量之和,而小兔子的数量就等于前一个月的成熟兔子数量。
- 以下不属于输出设备的是( )。
- A. 键盘
- B. 打印机
- C. 显示器
- D. 音响
正确答案:A. 键盘
解析:
计算机系统中,设备可以分为输入设备、输出设备、存储设备和处理器等。
- 输入设备:将人们熟悉的信息形式转换为计算机能够识别和接受的信息形式,如键盘、鼠标、扫描仪等。
- 输出设备:将计算机处理后的信息转换为人们熟悉的信息形式,如显示器、打印机、音响等。
- 存储设备:保存程序和数据,如硬盘、U盘、光盘等。
- 处理器:控制计算机的运行,执行各种运算和逻辑操作,如CPU。
根据以上定义,我们可以判断:
- 键盘是输入设备,用于将用户的操作输入到计算机中。
- 打印机是输出设备,将计算机处理后的信息打印到纸张上。
- 显示器是输出设备,将计算机处理后的信息以图形、文字等形式显示给用户。
- 音响也是输出设备,将计算机处理后的音频信息播放出来。
因此,以上选项中,不属于输出设备的是键盘,对应选项A。
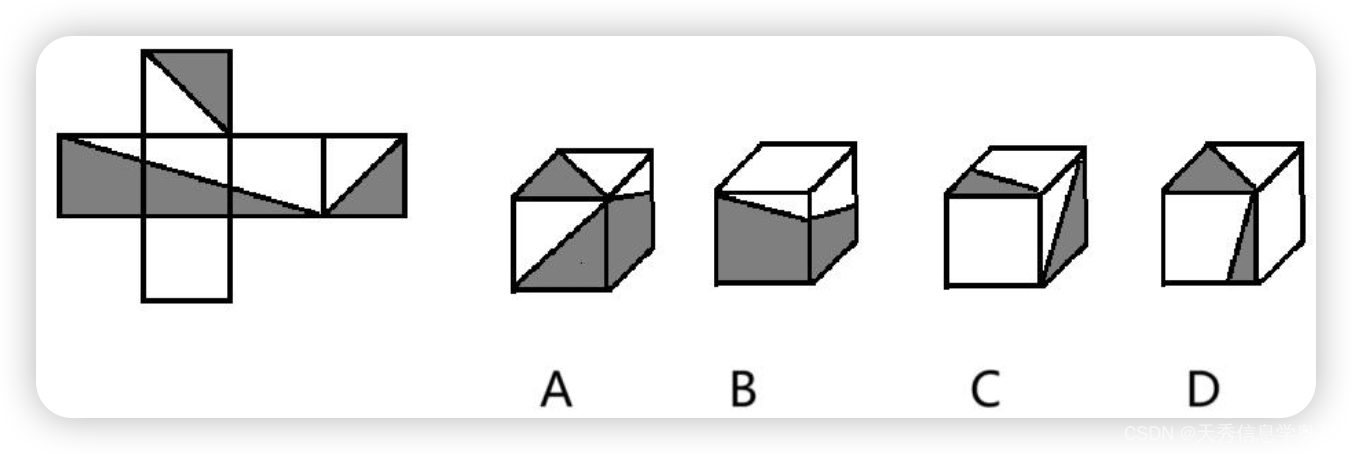
- 左边给定的是纸盒的外表面,右边哪一项是由它折叠而成( )。
正确答案:A
解析:
根据展开图得到的信息:
- B选项空白也应该在底面,上面应该是半开面
- C选项右边的半开应该是上面是阴影下面是白色
- D选项也是半开的那一面应该要反过来
- 小明和小红玩一个数字游戏。他们轮流报数,每次可以报1个或者2个数字,谁先报到30就赢了。如果小明先报数,并且两人都采用最佳策略,谁会赢得游戏?( )
- A. 小明肯定赢
- B. 小红肯定赢
- C. 平局
- D. 先报数的人肯定输
小明和小红玩一个数字游戏。他们轮流报数,每次可以报1个或者2个数字,谁先报到30就赢了。如果小明先报数,并且两人都采用最佳策略,谁会赢得游戏?
选项:
- A. 小明肯定赢
- B. 小红肯定赢
- C. 平局
- D. 先报数的人肯定输
正确答案:A. 小明肯定赢
解析:
这个问题是典型的取石子游戏,可以通过倒推法来分析。
- 如果轮到某个玩家报数时,他能直接报到30,则这个玩家立即获胜。
- 我们可以从较小的数字开始倒推,看在每个数字上报数的玩家如何确保最终获胜。
考虑在游戏接近尾声的情况:
- 如果轮到某人在数字29时报数,他可以报1个数字赢得游戏。
- 如果在数字28时报数,他可以报2个数字赢得游戏。
我们继续倒推:
- 在数字27时,无论报1个还是2个数字,都会使对方处在28或29的位置,对方可以直接赢得游戏。
通过这种方法,我们可以找出在哪些数字报数可以控制游戏的走向以确保获胜。最终,我们可以发现:
- 当数字是4的倍数时,报数的玩家将会处于劣势,因为无论他报1个还是2个数字,对手都可以调整报数使得数字回到4的倍数。
最初,小明先报数,他可以从0开始报数。他应该首先报1个数字,这样数字变为1(不是4的倍数)。之后,无论小红如何报数,小明都可以通过调整自己报的数字数量,最终使小红面对一个数字是4的倍数的局面。这样,小明可以控制游戏直到报数到达30。
因此,小明采用最佳策略时将确保获胜。