1.平方数

水题直接看代码
代码:
#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
#include<math.h>
#include<algorithm>
using namespace std;
typedef long long ll;
int main() {
ll x;
cin >> x;
ll a = sqrt(x);
if (abs(a * a - x) < abs((a + 1) * (a + 1) - x)) {
cout << a * a << endl;
}
else {
cout << (a + 1) * (a + 1) << endl;
}
return 0;
}
2.分组
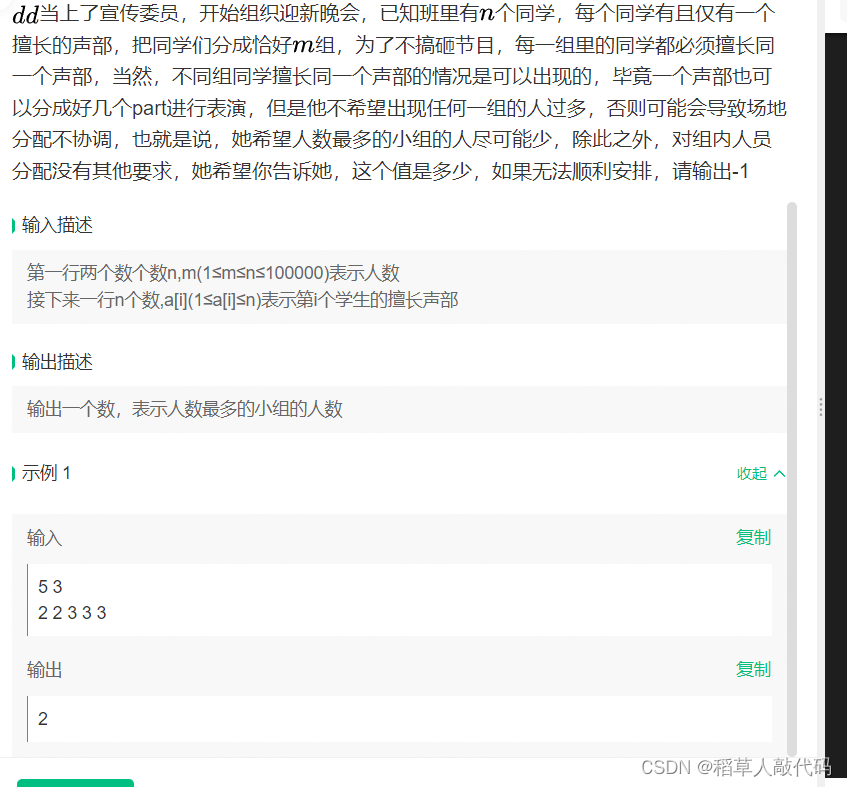
思路:
一眼二分。一般来说,遇到什么最大属性集合里面求最小都可以考虑用二分。
这题求人数最多的小组的人尽可能少。
我们将每一次分组情况都视为一次二分。每次二分的mid表示当前的所有分组中,拥有最多人数的组的人数。以此为基准,对所有的人进行分组,看能不能至少凑成m组,且这m组的每组最多人数不超过mid。
分组如何分呢?如果某一个声部的人数超过mid,我们就把超过的部分添加到新的一组去。如果人数小于或者等于mid,那就让他们一起为一组。
这样分可以得到以下结论:所有分组的最多人数不超过mid。且这样分组,组的数量是最少的。
如果按最少分组的数量都能大于m,说明我一定不能能把这些分组拆成恰好m个。
如果按最少分组的数量<m。无非就是从每组割一点人出来组成新的一组嘛。比如让一部分人一个人一组嘛。
我们把能分组成功的mid都放在右边。不能分组成功的都放在左边。
等到二分结束。r一定是在所有可以分组成功情况中的最左边。也就是,r是所有成功分组情况中,组内人数最多的值里面最小的。
此外如果r没有动,那就说明根本就没有mid可以分组成功。
代码:
#include <iostream>
#include<algorithm>
#include<unordered_map>
using namespace std;
const int N=1e5+10;
unordered_map<int,int> mp;
int mr;
int n;
int m;
bool check(int mid){//mid为人数最多的数量
if(mr<mid)return false;
int res=0;
for(auto it:mp){
if(it.second>mid){
res+=(it.second+mid-1)/mid;//向上取整
}else if(it.second<=mid){
res++;
}
}
if(res>m)return false;
return true;
}
int main() {
cin>>n>>m;
for(int i=1;i<=n;i++){
int x;
cin>>x;
mp[x]++;
mr=max(mr,mp[x]);
}
int l=0,r=mr+1;
while(l+1!=r){
int mid=(l+r)>>1;
if(check(mid))r=mid;
else l=mid;
}
if(r!=mr+1)cout<<r<<endl;
else cout<<-1<<endl;
return 0;
}
3.拓扑排序
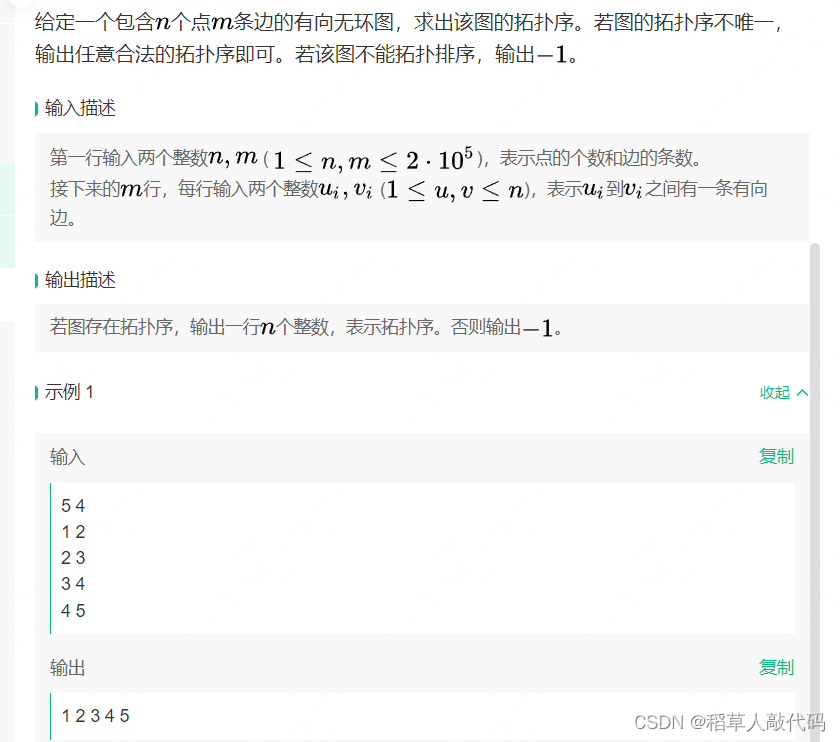
思路:拓扑排序的板子。先存一下边,再存一下每个点的入度。遍历每一条边,遍历的同时删除当前边,即入度减减。如果这个点的入度为0了,就入队列。拓扑排序保证,越早入队列的点,一定越在路径的前面。最后看一下是否每个点都入队列就行。
代码:
#include <iostream>
#include<vector>
#include<queue>
using namespace std;
const int N=2e5+10;
int n,m;
int d[N];
vector<int> ans;
bool topu(vector<vector<int>>& g){
queue<int> q;
for(int i=1;i<=n;i++){
if(d[i]==0){
ans.push_back(i);
q.push(i);
}
}
while(!q.empty()){
int t=q.front();
q.pop();
//cout<<t<<" kkk ";
for(auto it:g[t]){
d[it]--;
if(d[it]==0){
q.push(it);
ans.push_back(it);
}
}
}
//cout<<ans.size()<<endl;
if(ans.size()==n)return true;
return false;
}
int main() {
cin>>n>>m;
vector<vector<int>> g(n+1);
while(m--){
int a,b;
cin>>a>>b;
g[a].push_back(b);
d[b]++;
}
if(!topu(g))cout<<-1<<endl;
else {
for(int i=0;i<ans.size();i++){
if(i!=ans.size()-1)cout<<ans[i]<<" ";
else cout<<ans[i];
}
}
return 0;
}