正态分布，也称为高斯分布，是统计学中最重要的分布之一，具有许多重要的特性。正态分布的参数包括均值（μ）和标准差（σ），有时也使用==方差（σ^2）==来描述。下面是这些参数的意义及其在正态分布中的作用：

1. 均值（μ）：正态分布的均值表示数据的中心位置。它是所有数据点的平均值，对称分布的中心点。在正态分布中，均值也是分布的对称轴。当均值发生变化时，正态分布曲线会沿着 x 轴移动，但形状保持不变。
2. 标准差（σ）：标准差衡量数据的离散程度，即数据点偏离均值的程度。标准差越大，数据点分布越分散；标准差越小，数据点越集中。标准差决定了正态分布曲线的宽度，具体来说，约 68% 的数据点落在均值加减一个标准差之内，约 95% 的数据点落在均值加减两个标准差之内，约 99.7% 的数据点落在均值加减三个标准差之内。
3. 方差（σ^2）：方差是标准差的平方，表示数据与其均值之间的差异程度的平均值。它与标准差具有相同的信息，但通常在数学推导和处理中更方便。
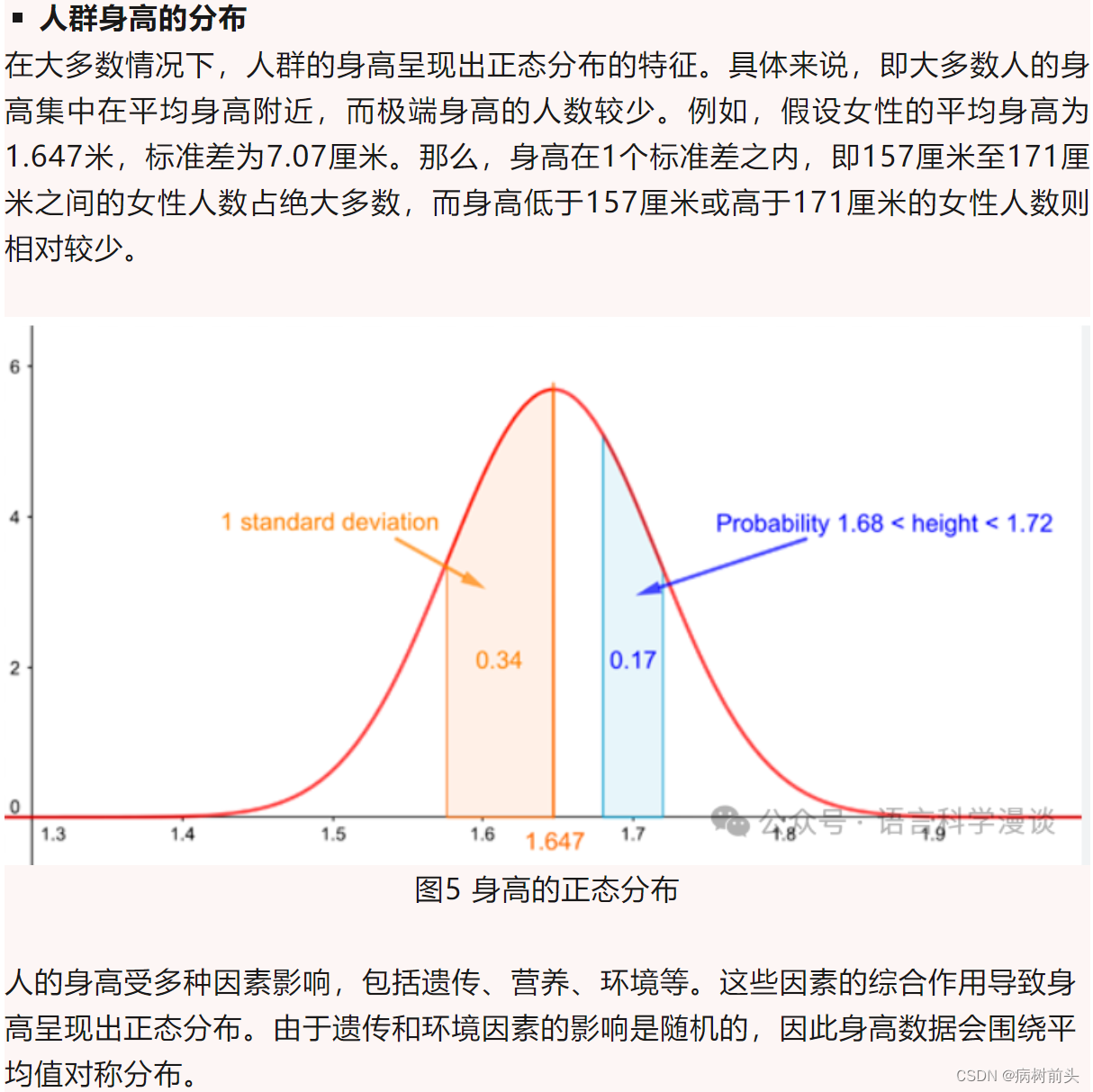
   正态分布是许多自然现象的模型，例如人的身高、考试成绩、温度变化等。在统计学和概率论中，正态分布具有重要的地位，因为许多常见的随机变量都近似服从正态分布，而且许多统计推断方法也基于对正态分布的假设。

正态分布的例子


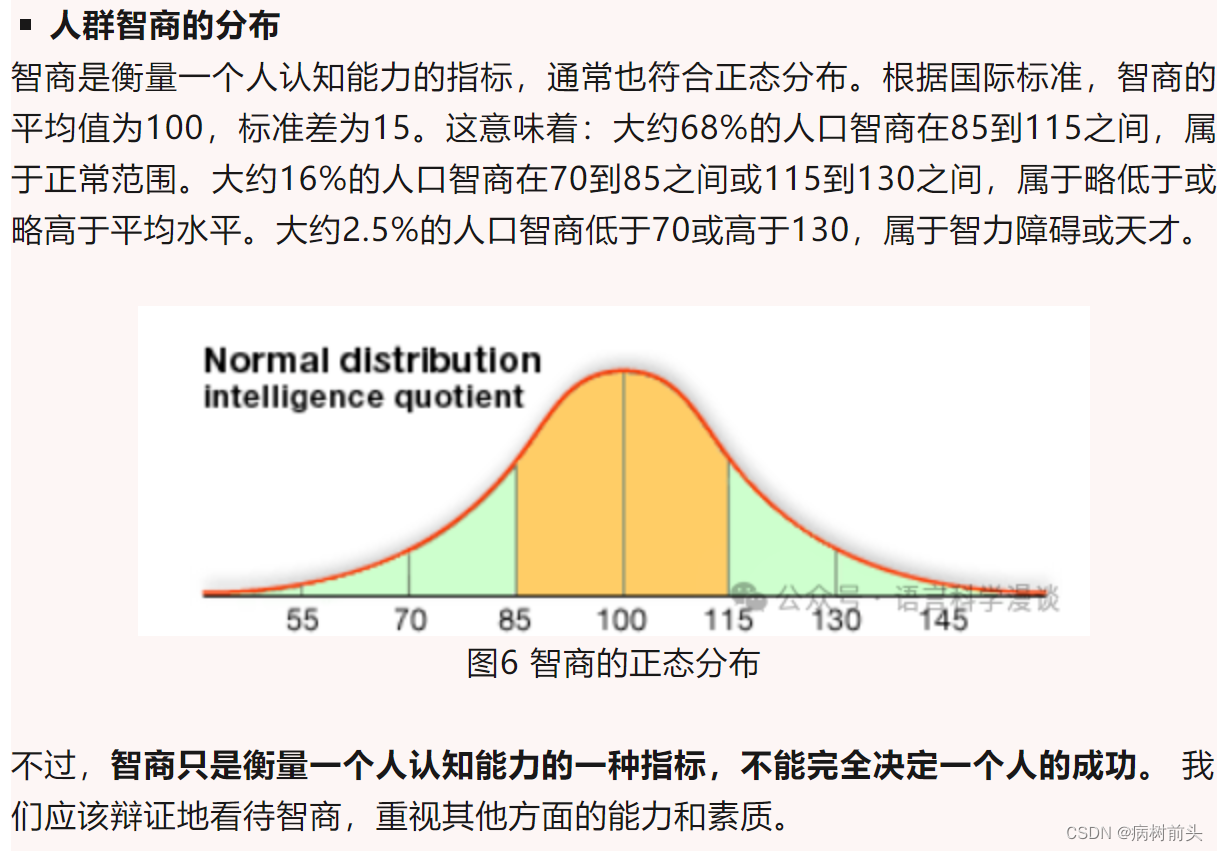
正态分布有三个特殊的比例值：68.27%、95.45%和99.73%。这三个比例值分别代表了正态分布曲线下三个不同区域的面积：

68.27%
正态分布曲线中，位于平均值正负一个标准差范围内的面积约为68.27%。这意味着，在一个服从正态分布的人群中，大约有68.27%的人的智商在平均值正负一个标准差之间。
95.45%
正态分布曲线中，位于平均值正负两个标准差范围内的面积约为95.45%。这意味着，在一个服从正态分布的人群中，大约有95.45%的人的智商在平均值正负两个标准差之间。
99.73%
正态分布曲线中，位于平均值正负三个标准差范围内的面积约为99.73%。这意味着，在一个服从正态分布的人群中，大约有99.73%的人的智商在平均值正负三个标准差之间。