题目链接:
141. 环形链表 - 力扣(LeetCode)
142. 环形链表 II - 力扣(LeetCode)
141.环形链表
方法思路:快慢指针
代码:
class Solution {
public:
bool hasCycle(ListNode *head) {
if(!head)
{
return false;
}
ListNode * slow=head;
ListNode * fast=head;
while(fast && fast->next)
{
slow=slow->next;
fast=fast->next->next;
if(fast==slow)
{
return true;
}
}
return false;
}
};解析:
用到了快慢指针,定义两个指针,slow指针和fast指针,令slow一次走一步,fast一次走两步,可以证明只要有环,则fast与slow一定能相遇。
证明:
1.fast一次走两步,slow一次走一步时:
假设一个环形链表如下:
令slow和fast初始都指向链表头结点head

---------------------------------------------------------------------------------------------------------------------------------
slow进环后,fast开始追击slow

---------------------------------------------------------------------------------------------------------------------------------
某一时刻时就会相遇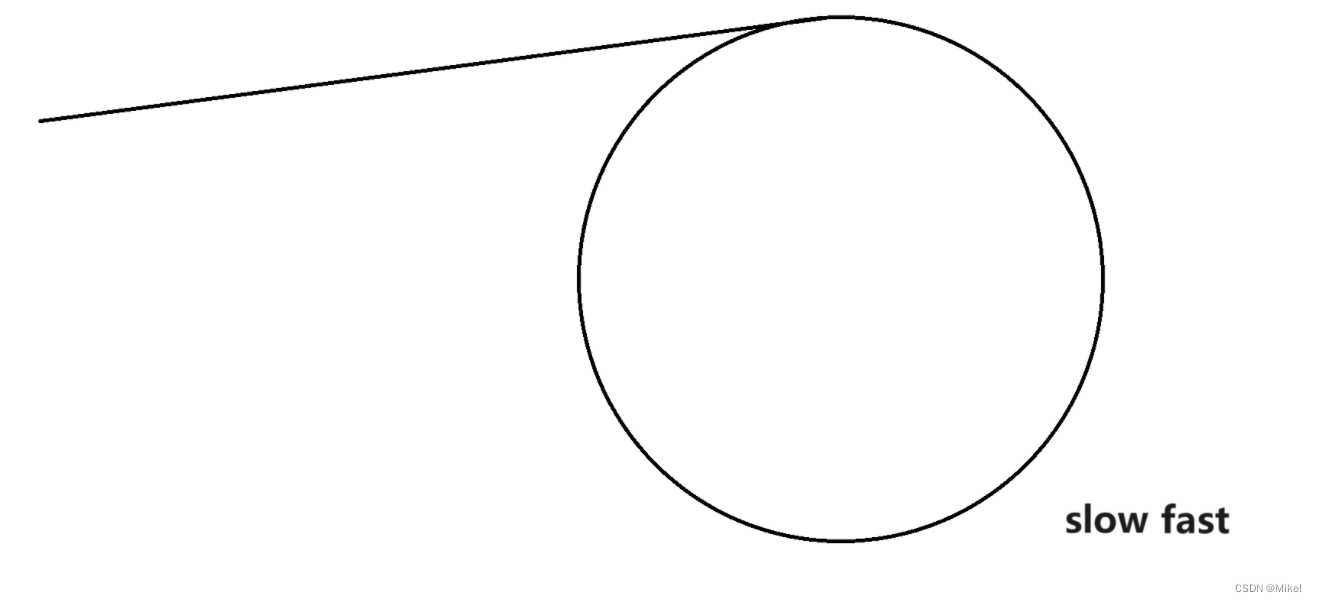
---------------------------------------------------------------------------------------------------------------------------------fast一次走两步,slow一次走一步,在环内一定可以相遇的证明:
(1).假设当slow刚进入环时,slow与fast距离差为N
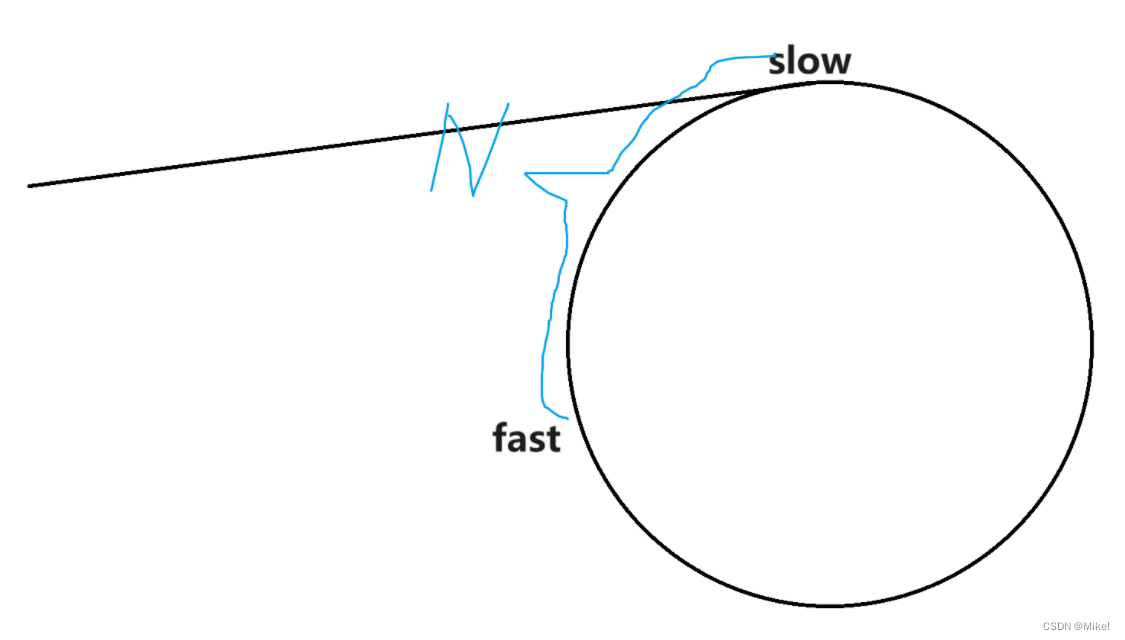
(2). 当fast一次走两步,slow一次走一步,则N变为了N-1,每追击一次,slow与fast之间的距离缩小1个距离,则N最终会变为0。则可证明slow与fast一定可以相遇。
2.fast一次走三步,slow一次走一步时:
(1).还是假设slow刚进环时,slow 与 fast相遇距离为N。
(2).fast走三步,slow走一步,距离变化为:
N-2 -> N-4 -> N-6..........以2递减。
(3).当N是2的倍数时,N最终会变为0,则可以相遇。
(4).当N不是2的倍数时,我们需要设环长为C。N会先变成-1,则fast超过了slow,如图:

则此时fast与slow的距离成为了C-1,则当C-1为2的倍数时,则slow与fast一定可以相遇。
结论:若N为2的倍数,则一定可以相遇。若N不是2的倍数时,当C为奇数时(C-1为偶数),一定可以相遇。
总结:
1.N是偶数,第一轮就追上了。
2.N是奇数,第一轮会错过,距离变为C-1
(1).如果C-1是偶数,下一轮就追上了。
证明是否永远追不上:
即N为奇数,C-1也为奇数时,是否存在?
先设环长为C,设当slow刚进环时,走了L距离,fast与slow距离为N,则fast已经在环内转了x圈。
则 slow走的距离:L fast走的距离:L+x*C+C-N;

又因为fast走的距离是slow的三倍,所以3*L=L+x*C+C-N
2*L=(x+1)*C-N
又因为假设N为奇数C为偶数时,则 2*L一定是偶数,则等号右侧也应该为偶数,但是(x+1)*C
为偶数,N为奇数,则右侧为奇数(偶数-奇数),显然出现矛盾,等号左侧一定是偶数,而等号右侧为奇数,所以出现矛盾。N为奇数且C为偶数不成立!!!即一定能追上!
结论:一定能追上
N为偶数时第一轮就追上了。
N是奇数时第一轮追不上,C-1是偶数第二轮就追上。
142.环形链表Ⅱ
方法思路:还是用快慢指针,找到快慢指针在环中相遇的结点,把这个结点存储起来,再令链表头结点和相遇的结点一起向前走,当头结点与相遇结点相遇时的结点,就是环的入口。
代码:
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode * fast=head;
ListNode * slow=head;
while(fast && fast->next)
{
fast=fast->next->next;
slow=slow->next;
if(fast==slow)
{
ListNode * next=fast;
while(next != head)
{
head=head->next;
next=next->next;
}
return next;
}
}
return NULL;
}
};证明:
当快指针一次走两次,慢指针一次走一次。
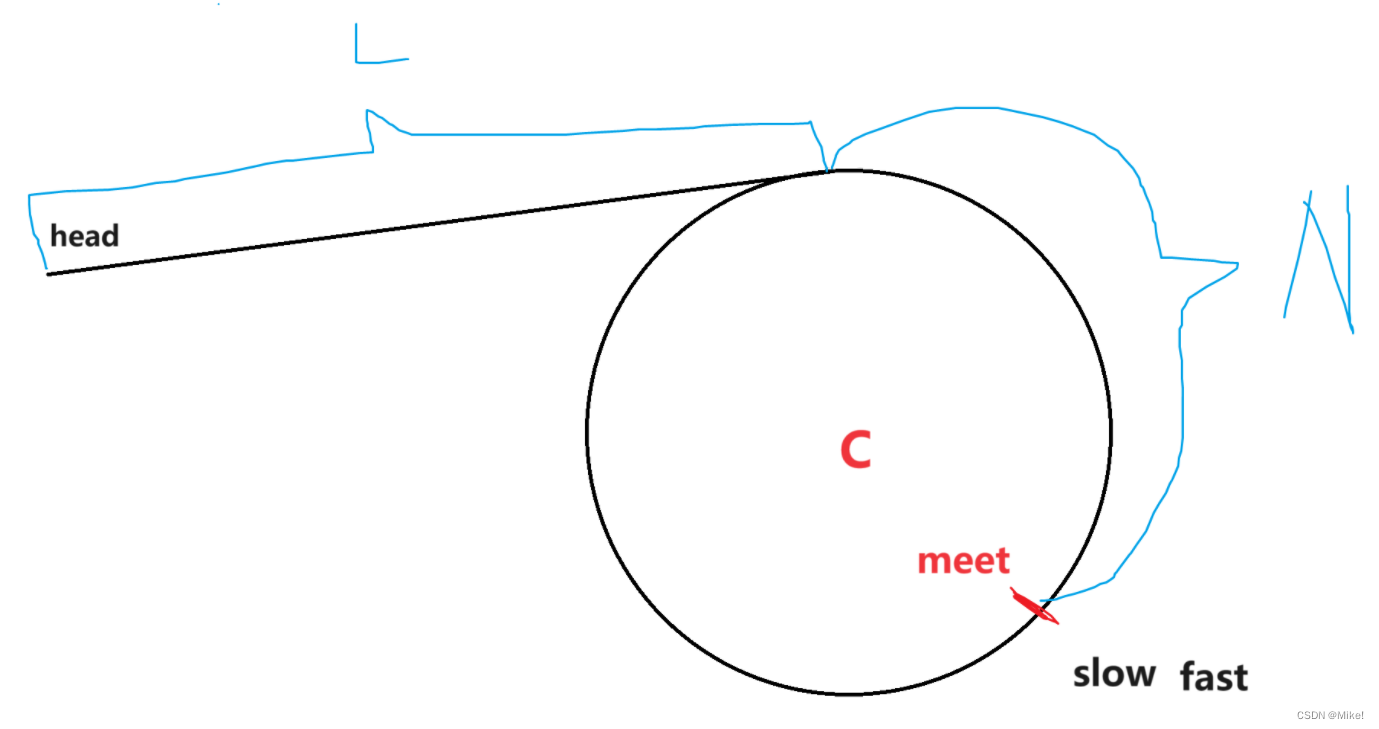
slow与fast相遇时 就证明L=C-N即可
slow 走的路程:L+N
fast 走的路程:L+x*C+N
因为fast的路程是slow的二倍,则2*(L+N)=L+x*C+N
L+N=x*C
L=x*C-N
当x=1时,则L=C-N
当x!=1时, 则由于C是圆环周长,则大于1圈的时候就相当于1圈,转整圈还是会到达meet处。
则可证明L=C-N成立
完结撒花