算法设计与分析4.1 迷宫问题 栈与队列解法、打印矩阵、三壶问题、蛮力匹配

news2024/11/25 4:50:11

1.ROSE矩阵

实现：

img

使用算法2

分析： 每半圈元素值的增长规律变换一次
设增量为t，每半圈变换一次t <— -t .
设矩阵边长为i，每半圈的元素个数是2*(i-1)个，hc为记数变量，则1≤hc<=2i-1，前1/4圈是1≤hc<=i-1，后1/4是i≤hc<=2i-2，若hc%i==0，则前1/4圈结果为0，后1/4结果为1，可表示为：index <— hc/i, hc <— hc+1。

计算模型：

设s[1]为矩阵行下标，s[0]为矩阵列下标。s数组下标为index。

t为下标增量，初值为-1，矩阵元素k∈[1,n*n].

1.index<- hc/i+1

2.hc<- hc+1

3.hc∈[1,2*i-1]

4.s[index]<-s[index]+t

5.a[s[1],s[0]]<- k , k<- k+1

6.当hc>2*i-1,i<- i-1 ,t<- -t

代码：

void rose(int n)
{
	int s[2];
	int a[n][n];
	int k=1,i=n,t=1;
	s[0]=-1,s[1]=0;
	while(k<=n*n)
	{
		for(int hc=1;hc<=2*i-1;++hc)
		{
			int index=hc/(i+1);
			s[index]+=t;
			a[s[1]][s[0]]=k;
			++k;
		}
		i--;
		t=-t;
	}
	for(int i=0;i<n;++i)
	{
		for(int j=0;j<n;++j)
		{
			cout<<a[i][j]<<"\t";
		}
		cout<<endl;
	}
}

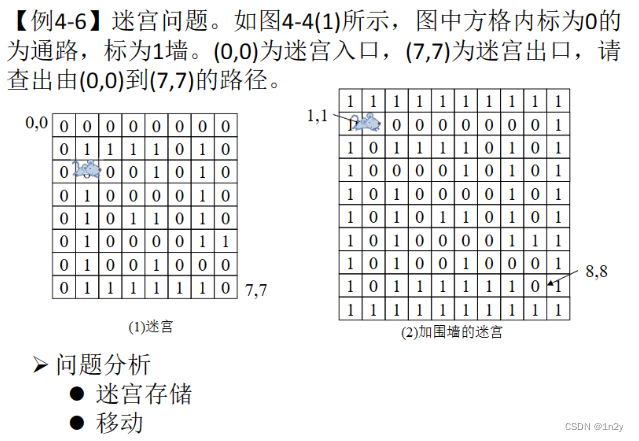
在这里插入图片描述

2.迷宫

在这里插入图片描述

最优路径？

可以使用栈或队列完成。

定义：

int M [ 10 ] [ 10 ] [10][10] [10][10]={
1,1,1,1,1,1,1,1,1,1,
1,0,0,0,0,0,0,0,0,1,
1,0,1,1,1,1,0,1,0,1,
1,0,0,0,0,1,0,1,0,1,
1,0,1,0,0,0,0,1,0,1,
1,0,1,0,1,1,0,1,0,1,
1,0,1,0,0,0,0,1,1,1,
1,0,1,0,0,1,0,0,0,1,
1,0,1,1,1,1,1,1,0,1,
1,1,1,1,1,1,1,1,1,1,} ;

//状态定义 ：
// M [ x ] [ y ] [x][y] [x][y]为0:通路 ，为1：墙 ， 为2：死路 ， 为3：已走过

int fx[]={-1,1,0,0};
int fy[]={0,0,-1,1};
typedef struct p
{
	int x,y;
	struct p* next;
}point;

1）.若使用栈：

主要代码：

void bfs()
{
	stack<point*>s;
	point *head=new point,*p;
	int x=1,y=1;
	head->x=x;
	head->y=y; 
	head->next=NULL;
	M[x][y]=3;
	s.push(head);
	int flag=0;
	while(!s.empty() )
	{
		p=s.top();
		s.pop();
		//cout<<"front:"<<p->x<<" "<<p->y<<endl;
		for(int i=0;i<4;++i)
		{
			y=p->y+fy[i];
			x=p->x+fx[i];
			if(M[x][y]==0)
			{
				//cout<<x<<" "<<y<<endl; 
				M[x][y]=3;
				point * newp=new point;
				newp->x=x;
				newp->y=y;
				newp->next=p;
				s.push(newp);
				if(x==8 && y==8)
				{
					flag=1;
					break;
				} 
			}
		}
		if(flag)break;	

​	} 
​	p=s.top();
​	while(p)
​	{
​		cout<<"("<<p->x<<","<<p->y<<")"<<"  ";
​		p=p->next;
​	}

}

具体实现：

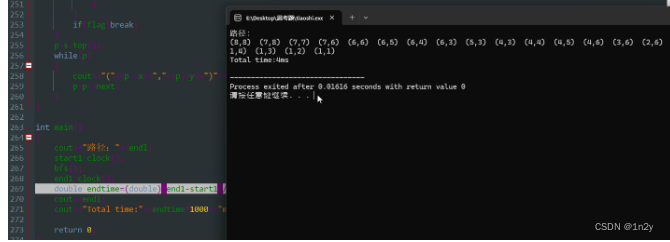
在这里插入图片描述

使用栈可以完成查找，但因其后入先出的特性，在程序实现中，优先对左上方的节点进行查找，针对此迷宫而言会产生一些不必要的路径。

所以若想最短时间得到最优路径可以使用队列。

2).队列实现：队列由于其先入先出的特点，每次都对右下方的点进行率先遍历，故更容易找到最优路径。

使用链表存储。

主要代码实现：

void bfs()
{
	m[x][y]=3;
	p=new po;
	p->x=x;
	p->y=y;
	p->pre=NULL;
	q.push(p);
	while(!q.empty() )
	{
		po * p1=q.front();
		q.pop();
		for(int i=0;i<4;i++)
		{
			po* pnew=new po;
			pnew->pre=NULL; 
			pnew->x =p1->x + fx[i];
			pnew->y = p1->y+ fy[i];
			if(m[pnew->x][pnew->y] ==0 )
			{
				m[pnew->x][pnew->y]=3;
				pnew->pre=p1;
				q.push(pnew);
			}
			if(pnew->x==8 && pnew->y==8)
				return;
		} 
	}

}

实现：
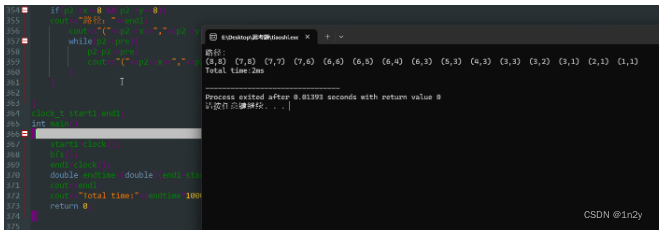
在这里插入图片描述

使用队列来实现，其时间为使用栈实现的一半左右。

3.三壶问题

在这里插入图片描述

BFS思想 穷举+回溯.

代码实现：

逐步模拟三个壶的倒水状态

typedef struct node
{
	int x,y,z;
	struct node * pre;
}node;
queue<node*>q;
node *p2;
node *p3;
set<int> cha;
bool is(node *p)
{
	if(p->x==4||p->y==4||p->z==4)
		return true;
	else 	return false;
}
void out(node *p)
{
	cout<<"("<<p->x<<","<<p->y<<","<<p->z<<")"<<endl;
}
void BFS()
{
	node *p=new node;
	p->x=8;p->y=0;p->z=0;
	p->pre=NULL;
	q.push(p);
	while(!q.empty())
	{
		node *p1=q.front();
		if(is(p1))	return;
		int x=p1->x;
		int y=p1->y;
		int z=p1->z;
		q.pop();
		if(cha.find(x*100+y*10+z)!=cha.end())  //没有任何一组状态使用此公式得到的计算结果是相同的，故用此来判别状态是否已被遍历 
			continue;
		else	cha.insert(x*100+y*10+z);
		if(x>0&&y<5)
		{
			p3=new node;
			if(x+y>5)
			{
				p3->x=x+y-5;
				p3->y=5;
			}
			else
			{
				p3->x=0;
				p3->y=x+y;
			}
			p3->z=z;
			p3->pre=p1;
			q.push(p3);
			if(is(p3))	return;
		}
		if(x>0&&z<3)
		{
			p3=new node;
			if(x+z>3)
			{
				p3->x=x+z-3;
				p3->z=3;
			}
			else
			{
				p3->x=0;
				p3->z=x+z;
			}
			p3->y=y;
			p3->pre=p1;
			q.push(p3);
			if(is(p3))	return;
		}
		if(y>0)
		{
			p3=new node;
			p3->x=x+y;
			p3->y=0;
			p3->z=z;
			p3->pre=p1;
			q.push(p3);
			if(is(p3))	return;
		}
		if(z>0)
		{
			p3=new node;
			p3->x=x+z;
			p3->z=0;
			p3->y=y;
			p3->pre=p1;
			q.push(p3);
			if(is(p3))	return;
		}
		if(y>0&&z<3)
		{
			p3=new node;
			if(y+z>3)
			{
				p3->y=y+z-3;
				p3->z=3;
			}
			else
			{
				p3->y=0;
				p3->z=y+z;
			}
			p3->x=x;
			p3->pre=p1;
			q.push(p3);
			if(is(p3))	return;
		}
		if(z>0&&y<5)
		{
			p3=new node;
			if(y+z>5)
			{
				p3->z=y+z-5;
				p3->y=5;
			}
			else
			{
				p3->z=0;
				p3->y=y+z;
			}
			p3->x=x;
			p3->pre=p1;
			q.push(p3);
			if(is(p3))	return;			
		}
	}
}

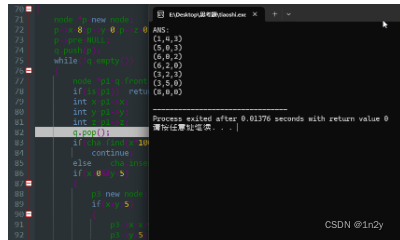
在这里插入图片描述

在这里插入图片描述

4.蛮力匹配

有A B两个字符串 ，长度为n和m

则其最差情况下：首先让A从第一个字符与B的各个字符进行比较，耗时m，A中共n个字符

耗时：O((n-m-1)*m)

5.相当于全排列，则共需 T(n)=O( (n-1)! )时间

6.经计算：15！=1307674368000

16！=20922789888000

18！=6402373705728000

19！=121645100408832000

1小时 运算：3.6* 1 0 13 10^{13} 1013次 16个城市

24小时 运算8.64* 1 0 14 10^{14} 1014次 17个城市

1年运算3.1536* 1 0 17 10^{17} 1017次 19个城市

100年运算3.1536* 1 0 19 10^{19} 1019​次 20个城市

  1. BFS时间复杂度分析

使用邻接表完成

对于 G 令 vexnum=n 即节点数量为n 对于邻接表：共e条边

则其所需时间共分为两部分，n个节点需要O(n)的复杂度，

而邻接表需O(e)的复杂度~ 总时间复杂度为O(n+e).

8.背包问题

1）时间复杂度

单纯通过穷举法，则：对于n个物品，会有 2 n − 1 2^{n-1} 2n−1种解 时间复杂度为 O ( 2 n ) O(2^{n}) O(2n)

2）改进

动规

int main()
{
    int N, V;
    cin >> N >> V;
    vector<int> v(N + 1), w(N + 1), f(V + 1);
    for(int i = 1; i <= N; ++i)
        cin >> v[i] >> w[i];
    for(int i = 1; i <= N; ++i)
        for(int j = V; j >= v[i]; --j)
            f[j] = max(f[j], f[j - v[i]] + w[i]);
    cout << *max_element(f.begin(), f.end());
    return 0;
}

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

时间复杂度： O ( N ∗ V ) O(N*V) O(N∗V)​

贪心

对物品的： 价值/物品体积 进行排序，逐个判断其体积是否能被装下

int G()
{
  float temp=0;
  float result=0;
  float c1=8; 
for(int i=0;i<4;i++)
{
  for(i=0;i<4;i++)
  {
  if(temp<sortBest[i])
    temp=sortBest[i];
  }
  //cout<<"max(sortBest)="<<temp<<endl;
  for(i=0;i<4;i++)
  {
  if (temp==sortBest[i])
  sortBest[i]=0; 
  if (w[i]<=c1)
  result=result+v[i];
  c1=c1-w[i]; 
  }
}

在这里插入图片描述

时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn)

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1634634.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

海外仓的精细化运营：现状、建议和落地操作指南

海外仓的精细化运营：现状、建议和落地操作指南

在跨境电商飞速发展的今天&#xff0c;海外仓运营模式是否足够精细化&#xff0c;是海外仓企业能否赢得竞争的关键。除了单纯的提升仓储能力之外&#xff0c;还需要关注效率的提升、技术革新和管理战略的升级。 从数据上看&#xff0c;大部分海外仓在精细化管理道路上面临的主要…
阅读更多...
Spring AOP详解，简单Demo

Spring AOP详解，简单Demo

目录 一、Spring AOP 是什么&#xff1f; 二、学习AOP 有什么作用&#xff1f; 三、AOP 的组成 四、 Spring AOP 简单demo 一、Spring AOP 是什么&#xff1f; Spring AOP&#xff08;Aspect-Oriented Programming in Spring&#xff09;是Spring框架中的一个重要组件&…
阅读更多...
preg_match详解（反向引用和捕获组）

preg_match详解（反向引用和捕获组）

在讲preg_match函数之前&#xff0c;我们先了解一下什么是php可变变量 php可变变量 在PHP中双引号包裹的字符串中可以解析变量&#xff0c;而单引号则不行 也就是在php中&#xff0c;双引号里面如果包含有变量&#xff0c;php解释器会将其替换为变量解释后的结果&#xff1b…
阅读更多...
基于 SpringCloud 的在线交易平台乐优商城的设计与实现（三）

基于 SpringCloud 的在线交易平台乐优商城的设计与实现（三）

基于 SpringCloud 的在线交易平台乐优商城的设计与实现 第3章 系统分析与设计3.1 系统基本功能描述3.2 可行性分析3.3 系统需求分析3.3.1 商家功能3.3.2 消费者功能&#xff1a;3.3.3 系统功能要求3.3.4 系统运行环境 3.4 系统开发工具3.4.1 IntellijIDEA3.4.2 Mysql3.4.3 Mave…
阅读更多...
C/C++ 入门（9）编译链接

C/C++ 入门（9）编译链接

个人主页&#xff1a;仍有未知等待探索-CSDN博客 专题分栏&#xff1a;C 目录 一、域 1、分类 2、搜索顺序 二、编译链接 1、代码在形成可执行文件的过程 2、符号表 三、问题 1、带有缺省参数的函数声明和定义分离 一、域 1、分类 域&#xff1a;全局域、局部域、命…
阅读更多...
第12章 消息服务

第12章 消息服务

第12章 消息服务 12.1 JMS1. 简介2. ActiveMQ安装Linux安装命令 3. 整合SpringBoot ****************************************************** 12.1 JMS 1. 简介 2. ActiveMQ安装 Linux安装命令 //下载 wget http://mirrors.hust.edu.cn/apache/activemq/5.15.16/apache-acti…
阅读更多...
JAVA系列 小白入门参考资料 类和对象（2）

JAVA系列 小白入门参考资料 类和对象（2）

目录 小引 1. this this引用 this的特性 this的使用 2. 对象的构造及初始化 如何初始化对象 构造方法 利用构造方法初始化对象的三种方式 方式一 方式二 方式三 直接初始化 小引 上一篇文章我们讨论到 如果创立类和对象&#xff0c;并且如何实例化对象和怎样…
阅读更多...
Vue+Element UI el-progress进度条内显示自定义数字及文字

Vue+Element UI el-progress进度条内显示自定义数字及文字

需求 进度条内展示 具体的数字值&#xff0c;进度条外展示 百分比数值 数据 data() {return {reNum: 3214,rePer:40,warmPer: 40,warmNum:2132,}}因为样式要求&#xff0c;显示的百分数也是自己写的哈 &#xff0c;没有用进度条自带的 代码 <div class"pick"&g…
阅读更多...
Java学习3：程序流程控制

Java学习3：程序流程控制

Java程序流程控制 1.执行顺序 顺序结构分支顺序 if,switch 循环结构 for ,while ,do-while 2.if分支 三种形式 if(条件表达式){} else if(){} else{}3.switch分支 string week "周一"; switch(week){case "周一":stem.out.println("周一&qu…
阅读更多...
六西格玛黑带考试：一场心灵与智慧的较量

六西格玛黑带考试：一场心灵与智慧的较量

终于踏过了六西格玛黑带考试这座大山&#xff0c;心中的激动与释然如波涛汹涌。这场考试&#xff0c;不仅仅是对我知识的检验&#xff0c;更是对我毅力与决心的考验。 备考的日子里&#xff0c;我仿佛进入了一个全新的世界。从统计学的深邃到流程优化的细致&#xff0c;每一个…
阅读更多...
C++入门第二节

C++入门第二节

点赞关注不迷路&#xff01;&#xff0c;本节涉及c入门关键字、命名空间、输入输出... 1. C关键字 C总计63个关键字&#xff0c;C语言32个关键字 asmdoifreturntrycontinueautodoubleinlineshorttypedefforbooldynamic_castintsignedtypeidpublicbreakelselongsizeoftypenam…
阅读更多...
在STM32上实现嵌入式人工智能应用

在STM32上实现嵌入式人工智能应用

引言 随着微控制器的计算能力不断增强&#xff0c;人工智能&#xff08;AI&#xff09;开始在嵌入式系统中扮演越来越重要的角色。STM32微控制器由于其高性能和低功耗的特性&#xff0c;非常适合部署轻量级AI模型。 本文将探讨如何在STM32平台上实现深度学习应用&#xff0c;…
阅读更多...
【活动】AIGC 技术的发展现状与未来趋势

【活动】AIGC 技术的发展现状与未来趋势

&#x1f308;个人主页: 鑫宝Code &#x1f525;热门专栏: 闲话杂谈&#xff5c; 炫酷HTML | JavaScript基础 ​&#x1f4ab;个人格言: "如无必要&#xff0c;勿增实体" 文章目录 AIGC 技术的发展现状与未来趋势引言AIGC技术的发展现状文本生成图像生成音频生成…
阅读更多...
Git中单独的功能特性分支是什么含义

Git中单独的功能特性分支是什么含义

在Git中&#xff0c;一个"功能特性分支"&#xff08;通常简称为“特性分支”&#xff09;是指从主开发分支&#xff08;比如main或master&#xff09;独立出来的分支&#xff0c;专门用于开发一个新功能、修复一个bug&#xff0c;或者进行实验性的尝试。使用特性分支…
阅读更多...
【Python BUG】connect: permission denied.

【Python BUG】connect: permission denied.

问题描述 解决方案 本质是权限问题 sudo密码即可
阅读更多...
​基于Python的在线自主评测系统(django)​

​基于Python的在线自主评测系统(django)​

基于Python的在线自主评测系统(django) 开发语言:Python 数据库&#xff1a;MySQL所用到的知识&#xff1a;Django框架工具&#xff1a;pycharm、Navicat、Maven 学生功能模块的实现 学生注册的实现 学生登录界面首页 在线考试界面 考试成绩查看界面 教师功能模块的实现 新建…
阅读更多...
用什么模型算法可以预测足球胜平负

用什么模型算法可以预测足球胜平负

预测足球胜平负的模型算法有很多种&#xff0c;每种算法都有其特点和适用场景。以下是一些常见的模型算法&#xff1a; Elo预测法&#xff1a; 这是一种通过研究主客场球队在比赛前的积分情况来预测胜负的方法。Elo预测法通过计算两队之间的积分差&#xff0c;根据特定的公式&…
阅读更多...
工业互联网通讯协议—欧姆龙(Fins tcp)

工业互联网通讯协议—欧姆龙(Fins tcp)

一、场景 近期公司要对欧姆龙CP系列设备的数据采集&#xff0c;于是就研究了下欧姆龙的Fins Tcp协议。 二、Fins Tcp 组成字节说明固定头446494E53 FINS对应的ASCII码的十六进制长度4后面剩余指令的长度命令4 握手固定为&#xff1a;00000000 读写固定为&#xff1a;0000000…
阅读更多...
http 协议的状态码有哪些？含义是什么？

http 协议的状态码有哪些？含义是什么？

http 协议的状态码有哪些&#xff1f;含义是什么&#xff1f; 一、http 协议的状态码类别二、常见的http 协议状态码及其含义 &#x1f496;The Begin&#x1f496;点点关注&#xff0c;收藏不迷路&#x1f496; http 协议是互联网上应用最为广泛的协议之一&#xff0c;而http …
阅读更多...
力扣HOT100 - 22. 括号生成

力扣HOT100 - 22. 括号生成

解题思路&#xff1a; class Solution {List<String> res new ArrayList<>();public List<String> generateParenthesis(int n) {if (n < 0) return res;getParenthesis("", n, n);return res;}private void getParenthesis(String str, int …
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023